勒让德变换与半二次优化方法
编辑勒让德变换
定义
勒让德变换(Legendre Transform,LT)或称作凸共轭(Convex Conjugate,CC),是凸分析中的一个基本工具,广泛用于优化理论中,它将一个函数f(x) 映射为另一个凸函数f^*(t)
在进行 LT 之前,我们需要确保原函数f 满足以下两个条件:
严格凸性(strictly convex): 函数f(x) 是严格凸的。
可导性(differentiability): 函数f(x) 至少一次可导(一般要二次导)。
因此通过 勒让德变换,我们就可以得到一个新的函数f^*
其中, \sup 表示取上确界(supremum),也就是取x t - f(x) 的最大值,因此我们可以得到:
说明f^*(t) 是所有x t - f(x) 的上界
我们再将f(x) 移到右边,可得:
这体现了f^*(t) 和f(x) 的对偶性
性质
我们现在关注勒让德变换在函数的横向伸缩(dilatation)、平移(shift)、以及纵向平移和伸缩的情况下的性质变化
(a) 横向伸缩 (Horizontal Dilatation):
设 \gamma > 0 是横向伸缩系数,定义一个新函数g(x):
对应的勒让德变换为:
横向缩放(乘以 \gamma)会导致勒让德共轭中的自变量t 被缩放为\frac{t}{\gamma}
证明
我们有:
目标是推导g^*(t) 的表达式,根据勒让德变换的定义,我们可得:
代入g(x) = f(\gamma x):
我们给x t 这部分配项,乘 \gamma 除 \gamma,可得
将 \gamma x 保存好,得到f(\gamma x) 的 LT 变换, g^*(t) 等于:
我们发现,
不用管u 是什么,只要一样就可以了,所以我们对比两个形式,观察到 \sup_{x \in \mathbb{R}} \bigl[ \gamma x \cdot \tfrac{t}{\gamma} - f(\gamma x) \bigr] 正是函数 f^*\bigl(\tfrac{t}{\gamma}\bigr) 的定义,因此:
注意一点, \gamma > 0 的条件是必要的,这是为了保证变换方向和凸性不改变。
(b) 横向平移 (Horizontal Shift):
设 x_0 \in \mathbb{R} 是横向平移的位移量,定义:g(x) = f(x - x_0) 对应的勒让德变换为:
对x 进行平移,相当于在勒让德共轭中增加一项线性修正x_0 t。
证明
定义:g(x) = f(x - x_0)
目标是推导g^*(t) 的表达式,根据勒让德变换的定义:
g^*(t) = \sup_{x \in \mathbb{R}} \big[ x t - f(x - x_0) \big]换元,令
因此
并且当x \in \mathbb{R} 时, u \in \mathbb{R}。将x = u + x_0 带入原式:
展开括号:
g^*(t) = \sup_{u \in \mathbb{R}} \big[ u t + x_0 t - f(u) \big]
注意到x_0 t 是与u 无关的常数,因此可以从\sup 中提取出来:
g^*(t) = \sup_{u \in \mathbb{R}} \big[ u t - f(u) \big] + x_0 t
我们注意到,其中的\sup_{u \in \mathbb{R}} [u t - f(u)] 就是f^*(t) 的定义:
因此可以得到:
证毕
(c) 纵向平移和伸缩 (Vertical ShiftDilatation):
设 \alpha \in \mathbb{R} 和 \beta > 0 ,定义新的函数g(x) :
对应的勒让德变换为:
纵向伸缩 \beta 会缩放勒让德变换的自变量t ,并乘以 \beta。纵向平移 \alpha 直接导致勒让德共轭函数的值减去 \alpha。
证明
其中:
因此:
由于 \alpha 与x 无关:
将\sup 里面表达式 乘 \beta 除 \beta,可得:
我们注意到\sup_{x \in \mathbb{R}} \bigl[ \frac{t}{\beta} x - f(x) \bigr] 就是 f^*\Bigl( \tfrac{t}{\beta} \Bigr)的定义,即:
得到:
证毕
(d) 双重共轭恢复原函数
勒让德变换的一个关键性质,即双重共轭恢复原函数
证明
双重共轭函数定义为:
定义辅助函数h_t(x) :
对h_t(x) 求导,计算h_t^{\prime}(x) :
根据勒让德变换的性质:
因此:
令导数h_t^{\prime}(x) = 0 ,得:
将极值点代入
将\bar{x} = \chi(t) 代入h_t(x) :
根据勒让德变换的定义f^*(\bar{x}) = \bar{x} \chi(t) - f[\chi(t)] ,可以展开为:
化简得到:
由于\chi(t) = f^{\prime-1}(t) ,因此:
因此:
证毕
双重共轭性质表明,严格凸且下半连续的函数在进行两次勒让德变换后会恢复原函数。这一性质保证了勒让德变换的对偶性,因此在在优化问题中构造对偶关系来解决问题。
%% 双重共轭验证 f^{**}(x) = f(x)
x_test = linspace(1,2,200);
f_dd_star = zeros(size(x_test));
for i = 1:length(x_test)
x_val = x_test(i);
h_xt = @(tau) x_val*tau f_star_analytic(tau);
neg_h_xt = @(tau) h_xt(tau);
[~, h_min_val] = fminbnd(neg_h_xt, 10, 10);
f_dd_star(i) = h_min_val;
end
figure;
plot(x_test, f(x_test), 'b', 'LineWidth',2); hold on;
plot(x_test, f_dd_star, 'r','LineWidth',2);
xlabel('x','Interpreter','none');
ylabel('Function value','Interpreter','none');
legend({'f(x)','f**(x)'},'Interpreter','none','Location','best');
title('Double conjugate check: f**(x) vs f(x)','Interpreter','none');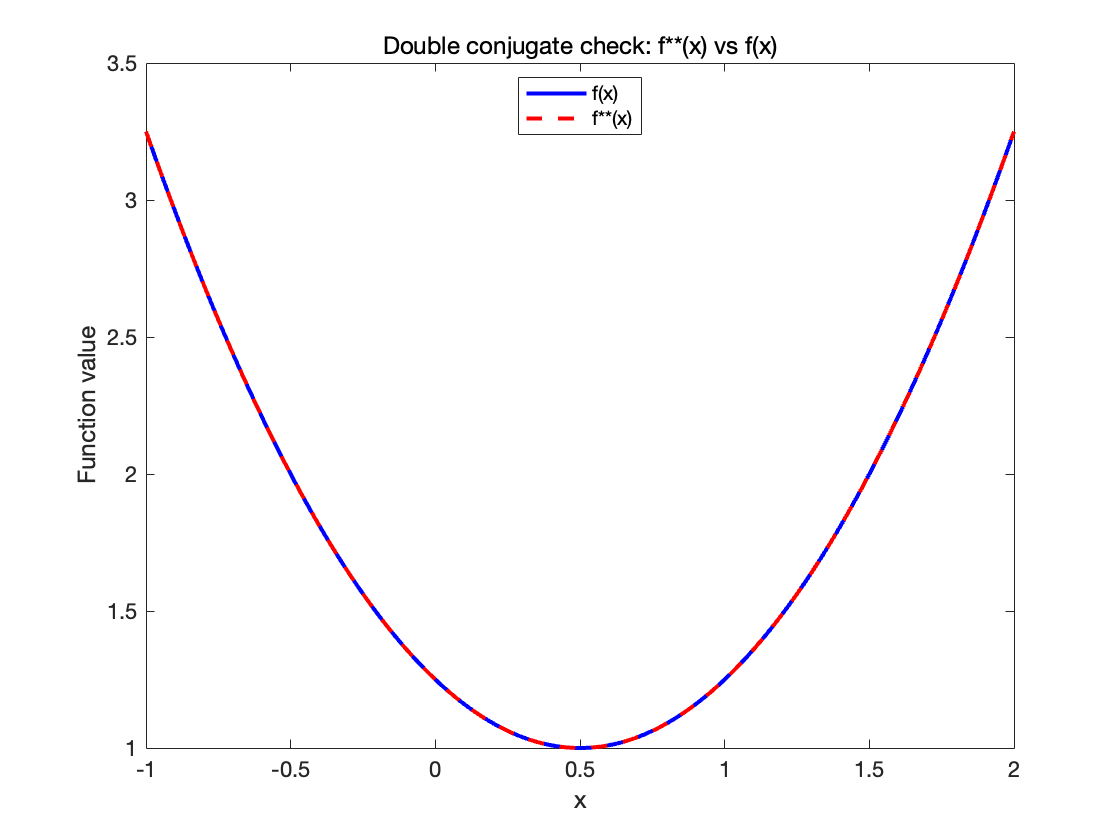
举例
下面我们以一个二次函数为例,详细计算推导它的勒让德变换(Legendre Transform, LT)
其中:
\alpha \in \mathbb{R} 是一个常数,表示垂直偏移;
\beta > 0 是参数,控制二次项的系数;
x_0 是偏移中心。
目标是找到其勒让德变换:
推导过程
我们先看里面x t - f(x) 这一项,因此定义辅助函数:
将f(x) 代入得到:
展开:
所以,原式等于:
我们希望在此基础上更进一步,也就是拿掉\sup 符号。为了完成这一点,需要找到内层函数g_t(x) 的极大值。
对g_t(x) 求导数并找到极值点
计算g_t^{\prime}(x) 的一阶导数:
令g_t^{\prime}(x) = 0 解出极值点:
计算g_t(x) 的二阶导数:
由于 \beta > 0,说明g_t(x) 是一个严格 concave 函数,因此在\bar{x} 处确实取得最大值。
将极值点代回g_t(x)
将\bar{x} = x_0 + \tfrac{t}{\beta} 代入g_t(x) :
具体代入:
展开化简:
进一步整理:
最终结果:
具体过程是:
1. 定义辅助函数g_t(x) = x t - f(x)
2. 求导数g_t^{\prime}(x) = t - f^{\prime}(x)
3. 找到零点\bar{x} = \chi(t)
4. 代回g_t(\bar{x}) 得到f^*(t)
求导
勒让德变换通用表达式为:
其中:\chi(t) 是f^{\prime}(x) 的反函数,即\chi(t) = (f^{\prime})^{-1}(t)。
一阶导数
为了求f^*(t) 的一阶导数,对f^*(t) 进行求导:
利用链式法则,得到:
由于\chi(t) = f^{\prime-1}(t),并且f^{\prime}[\chi(t)] = t,代入后有:
因此,一阶导数结果为:
f^{*\prime}(t) = \chi(t) = f^{\prime-1}(t)
勒让德变换的二阶导数
对f^{*\prime}(t) = \chi(t) 再求导:
由于\chi(t) = f^{\prime-1}(t),求导得到:
因此,勒让德变换的二阶导数为:
由于f^{\prime\prime}(x) > 0( f(x) 是严格凸函数),所以f^{*\prime\prime}(t) > 0,从而证明f^*(t) 始终是凸函数。
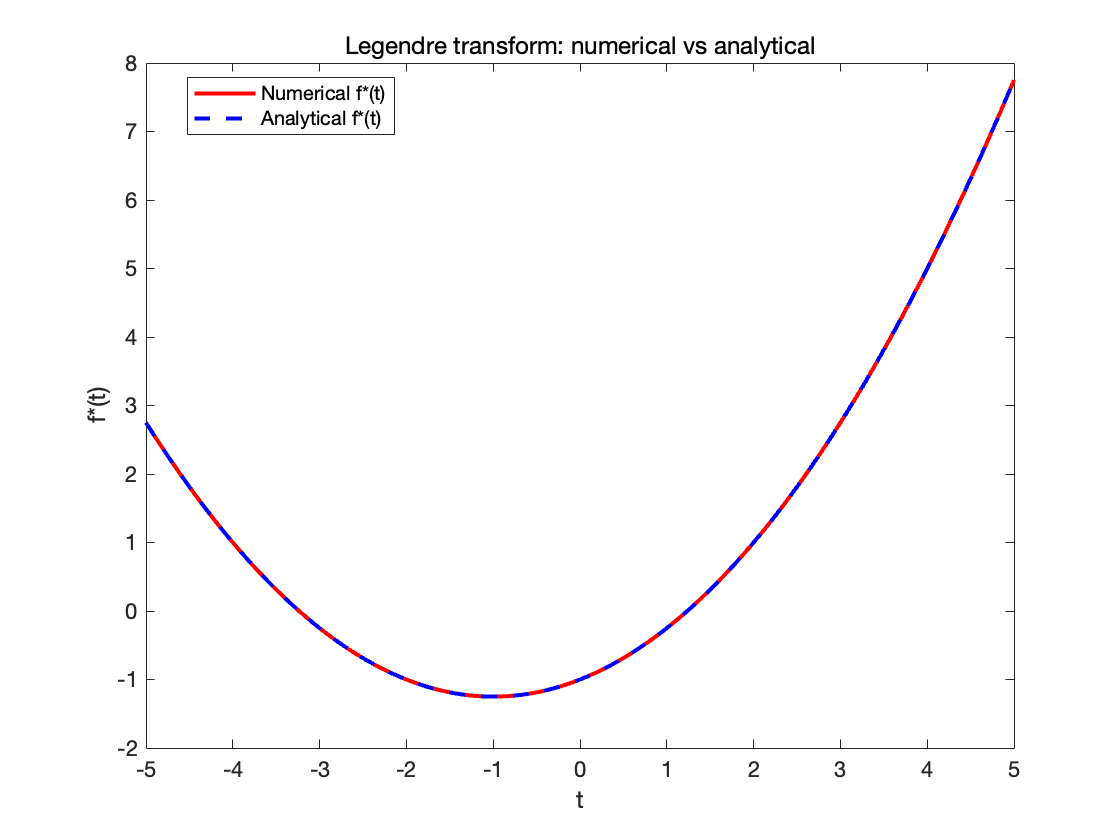
clear; close all; clc;
%% 参数设置 (用于勒让德变换及半二次分解示例)
alpha = 1.0; % f(x)的垂直偏移
beta = 2.0; % f(x)中二次项系数 > 0
x0 = 0.5; % f(x)中心偏移
% 定义原函数 f(x)
f = @(x) alpha + (beta/2)*(x x0).^2;
% 理论勒让德共轭 f*(t)
f_star_analytic = @(t) (t.^2)/(2*beta) + t*x0 alpha;
% 定义 t 和 x 的取值范围用于数值求解
t_vals = linspace(5,5,200);
x_vals = linspace(5,5,200);
%% 数值求勒让德变换 f*(t)
f_star_numeric = zeros(size(t_vals));
for i = 1:length(t_vals)
t = t_vals(i);
g_t = @(x) x*t f(x);
neg_g_t = @(x) g_t(x);
[~, fval_neg] = fminbnd(neg_g_t, min(x_vals), max(x_vals));
f_star_numeric(i) = fval_neg;
end%% 对比数值结果和解析解
figure;
plot(t_vals, f_star_numeric, 'r', 'LineWidth',2); hold on;
plot(t_vals, f_star_analytic(t_vals), 'b', 'LineWidth',2);
xlabel('t','Interpreter','none');
ylabel('f*(t)','Interpreter','none');
legend({'Numerical f*(t)','Analytical f*(t)'},'Interpreter','none','Location','best');
title('Legendre transform: numerical vs analytical','Interpreter','none');
半二次优化方法
理论
原始准则(Criterion)
定义的优化目标函数\mathcal{J}(x) 为:
第一项\| \mathbf{y} - \mathbf{H} \mathbf{x} \|^2 是数据拟合项,用来度量\mathbf{x} 和观测数据\mathbf{y} 之间的误差。
第二项\mu \sum_{p \sim q} \varphi(x_p - x_q) 是正则化项,用于惩罚相邻变量(如图像像素邻点)间的差异。
半二次优化的核心
核心是将非二次函数\varphi(\delta) 转化为带有辅助变量a 的二次形式。因此,我们为每个x_p - x_q 引入辅助变量a_{pq} ,使得:
其中, \zeta(a) 是一个自定义构造的函数。这种引入将非二次函数\varphi(\delta) 分解为关于变量a 的优化问题。
引入辅助变量后的扩展准则
原始准则扩展为:
新准则\widetilde{\mathcal{J}}(\mathbf{x}, \mathbf{a}) 现在是关于\mathbf{x} 和辅助变量\mathbf{a} 的联合优化问题。
原始准则与扩展准则的关系
这说明通过优化\widetilde{\mathcal{J}}(\mathbf{x}, \mathbf{a}) 的辅助变量\mathbf{a} ,可以间接得到原始问题的解。
为什么引入辅助变量?
这里一定有一个疑问:为什么一定要引入一个辅助变量呢?直接对原式进行运算不好吗?问题就在非二次函数\varphi(\delta) 上面。非二次的优化问题可能要处理复杂的非线性和非凸问题,很难求解。通过引入一个辅助变量,将非二次函数\varphi(\delta) 分解为二次形式和一个新的函数\zeta(a) ,这样就好优化多了。多引入一个变量a 也不要紧,可以分离\mathbf{x} 和\mathbf{a} ,固定一个,优化另一个,并且优化交替进行,通过迭代逐步收敛到全局最优解。
实现
%% 半二次分解示例 (Huber函数)
% 设置Huber函数阈值参数 s
s = 0.5;
varphi = @(delta) (abs(delta)<=s).* (delta.^2/2) + (abs(delta)>s).*(s*abs(delta)-s^2/2);
% g(delta) = (delta^2)/2 - varphi(delta)
g = @(delta) (delta.^2)/2 - varphi(delta);
% 数值上计算g*(a)
a_vals = linspace(-3,3,200);
g_star_vals = zeros(size(a_vals));
for i=1:length(a_vals)
a_ = a_vals(i);
h_a_delta = @(delta) g(delta)-a_*delta;
[~,h_min_val] = fminbnd(h_a_delta, -5,5);
g_star_vals(i) = -h_min_val;
end
% 定义zeta(a)=g*(a)-a^2/2
zeta = @(a) interp1(a_vals,g_star_vals,a,'linear','extrap') - a.^2/2;
% 检验半二次分解 varphi(delta)=inf_a[(delta - a)^2/2 + zeta(a)]
delta_test = linspace(-3,3,100);
varphi_recons = zeros(size(delta_test));
for i=1:length(delta_test)
delta_ = delta_test(i);
Phi = @(a) ((delta_-a).^2)/2 + zeta(a);
[~,Phi_min] = fminbnd(Phi,-5,5);
varphi_recons(i) = Phi_min;
end
figure;
plot(delta_test,varphi(delta_test),'b','LineWidth',2); hold on;
plot(delta_test,varphi_recons,'r--','LineWidth',2);
xlabel('delta','Interpreter','none');
ylabel('varphi(delta)','Interpreter','none');
legend({'varphi(delta)','Half-quadratic decomposition'},'Interpreter','none','Location','best');
title('Half-quadratic decomposition check','Interpreter','none');
disp('Legendre transform and half-quadratic decomposition demonstrations completed.');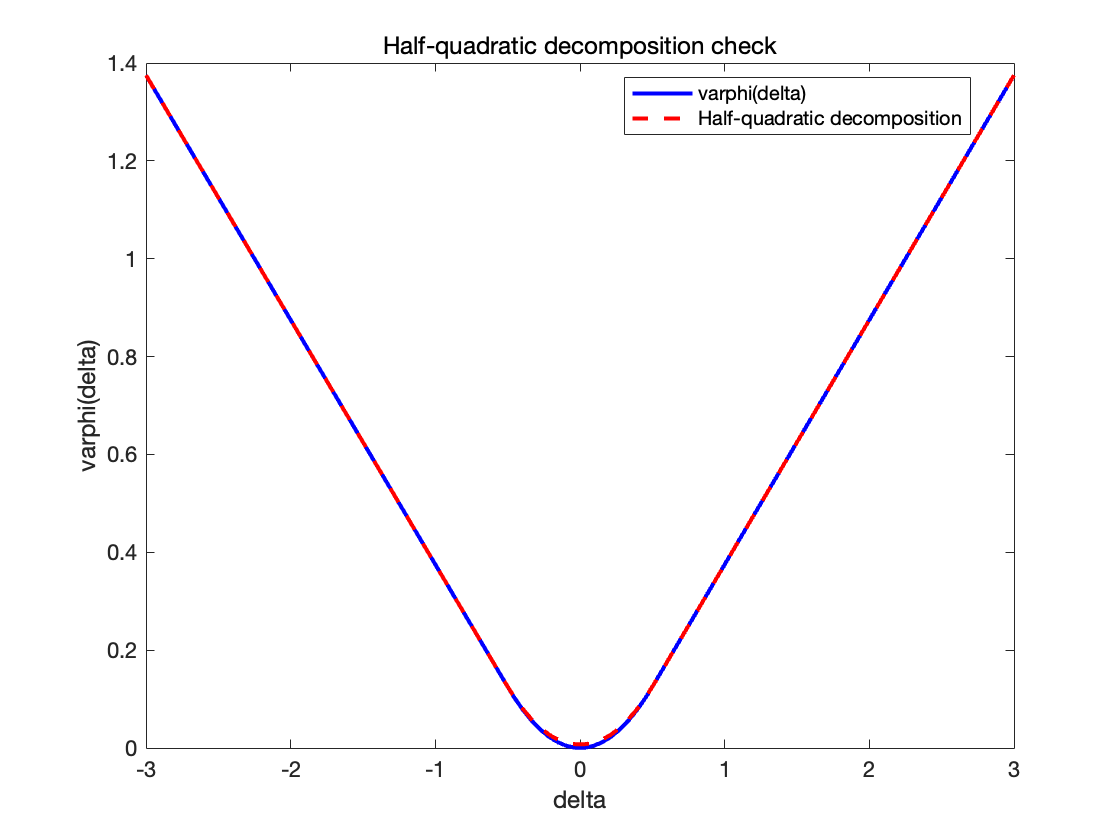
在半二次优化中引入勒让德变换
我们刚刚的思路非常美好,现在只需要分开优化就好了,但是现在我们有两个前置问题
\varphi(\delta) = \inf_a \left[ \frac{1}{2} (\delta - a)^2 + \zeta(a) \right] 怎么构建的?
\zeta(a) 怎么构建?
我们现在推导证明:
证明
引入一个新的辅助函数g(\delta) ,定义为:
这里g(\delta) 被设计为一个严格凸函数(二次项\frac{\delta^2}{2} 保证了凸性)。
我们对g(\delta) 应用勒让德变换g^*(a) :
代入g(\delta) = \frac{\delta^2}{2} - \varphi(\delta) ,勒让德变换展开为:
将辅助函数\zeta(a) 定义为:
代入g^*(a) 的表达式,得:
这表明\zeta(a) 是由\varphi(\delta) 和二次项\frac{ (\delta - a)^2 }{2} 的优化分解所定义的。
利用双重勒让德变换的性质g = g^{**} 的性质,我们可以写出
结合g(\delta) = \frac{\delta^2}{2} - \varphi(\delta) ,可以进一步推导出:
由上述方程,可以得到:
进一步等价为:
将g^*(a) 的定义代入:
重新整理:
这就得到了半二次分解的基本形式。
证毕
为了进一步分析辅助变量a,考虑优化问题:
对优化准则求导:
解出最优a = \bar{a}:
结合\zeta^{\prime}(a) = g^{\prime}(a) ,可以进一步得到:
或简化为:
通过上述推导,我们得到:
1. 半二次分解的标准形式:
其中\zeta(a) = g^*(a) - \frac{a^2}{2} 是辅助函数。
2. 最优辅助变量的表达式:
这个理论保证了对于任何给定的\varphi(\delta),我们都能通过构造辅助变量a 来优化原始函数。
总结
原始优化问题的目标函数为:
为了解决非二次项\varphi(x_p - x_q) ,引入辅助变量a_{pq} ,将原始准则扩展为:
a_{pq} 是辅助变量,用于解耦x_p 和x_q 。\zeta(a_{pq}) 是通过勒让德变换定义的辅助函数。
算法策略:交替优化
对\mathbf{x} 固定\mathbf{a} 进行优化
在固定\mathbf{a} 的情况下,优化目标函数变为关于\mathbf{x} 的二次问题:\widetilde{\mathbf{x}}(\mathbf{a}) = \arg\min_{\mathbf{x}} \widetilde{\mathcal{J}}(\mathbf{x}, \mathbf{a})这是一个标准的二次优化问题,可以通过解析解(如线性代数方法)或数值方法高效求解。
对\mathbf{a} 固定\mathbf{x} 进行优化
在固定\mathbf{x} 的情况下,优化目标函数变为关于\mathbf{a} 的问题:\widetilde{\mathbf{a}}(\mathbf{x}) = \arg\min_{\mathbf{a}} \widetilde{\mathcal{J}}(\mathbf{x}, \mathbf{a})这个优化问题也可以通过显式公式解出,因为\zeta(a) 是预定义的。
通过在这两个步骤之间交替迭代,逐步接近全局最优解。
变量的相互作用:
原始问题中的变量x_p 和x_q 存在耦合关系(通过\varphi(x_p - x_q)), 扩展准则通过引入a_{pq} ,解耦了变量\mathbf{x} 和\mathbf{a} ,从而简化了优化问题。优化问题的本质:
原始问题是非二次的,且变量相互作用,扩展后,尽管存在交互,但问题本质上是二次的,因此容易求解。
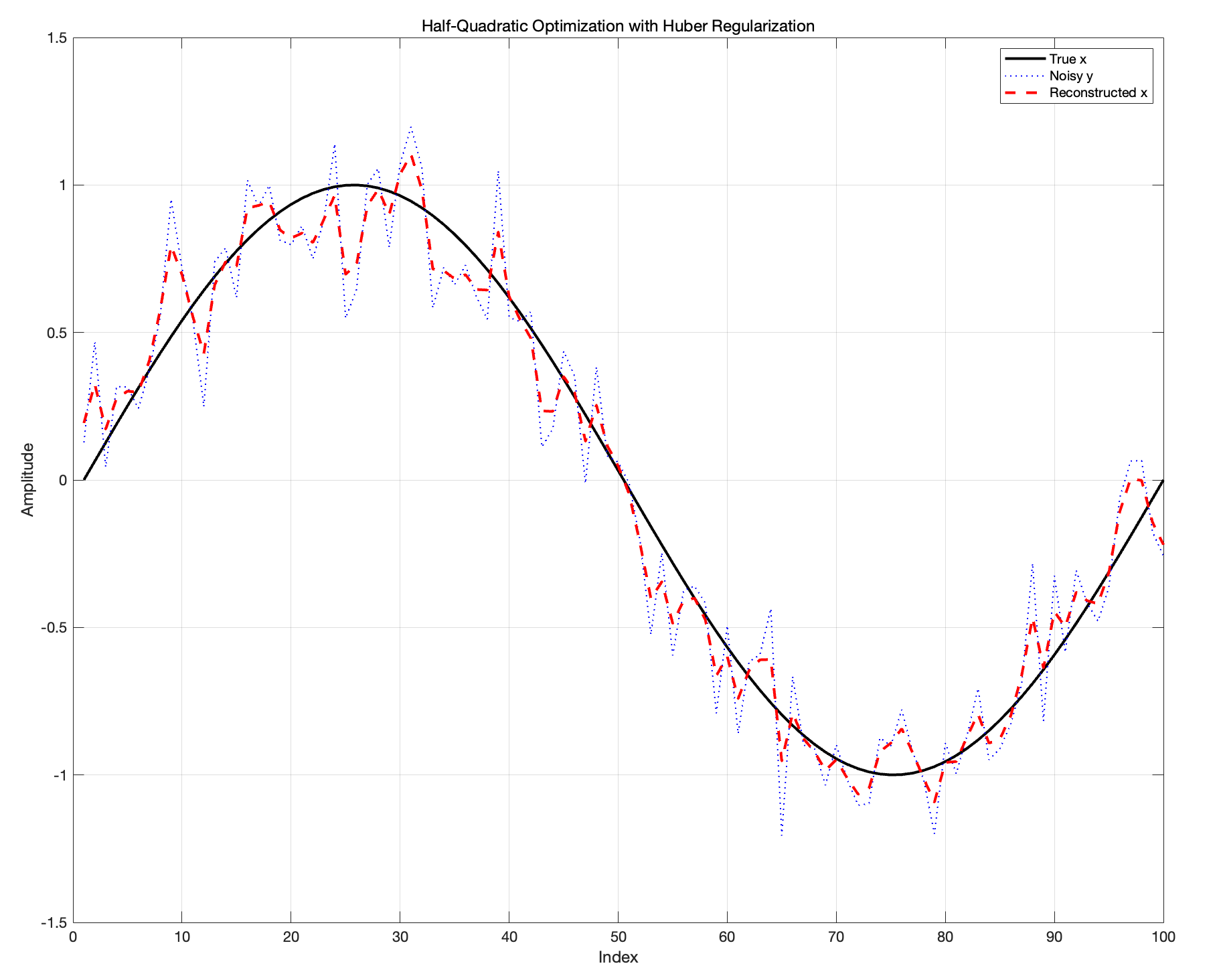
%% 半二次优化示例
% 注意:我们已定义 s 和 varphi,上述 s=0.5 也适用于此
% 新增phi_prime定义(在之前未定义,需新增)
phi_prime = @(delta) (abs(delta)<=s).*delta + (abs(delta)>s).*s.*sign(delta);
% 以下半二次优化1D信号示例
% 参数设置(对于优化问题)
N = 100; % 信号长度
mu = 1; % 正则化参数
maxIter = 50; % 最大迭代次数
% 生成观测数据 y (用 x_true 加噪声)
x_true = sin(linspace(0,2*pi,N))'; % 真值
noise = 0.1 * randn(N,1);
y = x_true + noise;
% 定义算子H为单位映射,这里H = I
H = eye(N);
% 定义初始值
x = y; % 初始解
a = zeros(N-1,1); % 辅助变量
% 构造差分矩阵 R (N-1 x N)
R = spdiags([ones(N-1,1), -ones(N-1,1)], [0,1], N-1, N);
% 系数矩阵A_x = 2I + mu R'R
A_x = 2*speye(N) + mu*(R'*R);
% 迭代求解
for iter = 1:maxIter
% Step 1: 固定 a 更新 x
rhs = 2*y + mu*R'*a;
x = A_x\rhs;
% Step 2: 固定 x 更新 a
delta = R*x;
a = delta - phi_prime(delta);
% 显示进度(每10次迭代显示一次)
if mod(iter,10)==0
phi_val = zeros(N-1,1);
for k=1:(N-1)
d = delta(k);
if abs(d)<=s
phi_val(k) = d^2/2;
else
phi_val(k) = s*abs(d)-s^2/2;
end
end
J_val = norm(y - x)^2 + mu*sum(phi_val);
fprintf('Iter %d, J = %f\n', iter, J_val);
end
end
% 结果展示
figure;
plot(x_true, 'k-', 'LineWidth',2); hold on;
plot(y, 'b:', 'LineWidth',1);
plot(x, 'r--', 'LineWidth',2);
legend('True x','Noisy y','Reconstructed x','Interpreter','none');
xlabel('Index','Interpreter','none');
ylabel('Amplitude','Interpreter','none');
title('Half-Quadratic Optimization with Huber Regularization','Interpreter','none');
grid on;