插值方法
编辑定义: 通过已知的、离散的部分数据点推算新数据点的方法,插值法常用于函数拟合中。
插值法是函数拟合的一种特殊情况,但它们有区别:
对应数据点:
我们现在的目的就是拟合出一个 f(x) 来估算未知的数据点。
线性插值
定义
如果我们有两个点 (x_0, y_0), (x_1, y_1) ,我们希望找到它们中间的一个未知的数据点 (x, y),其中x_0 \leq x \leq x_1,那么线性插值就是直接假设(x, y) 落在这两点之间的直线上,换句话说,我们拟合了一条直线 f(x),其斜率m为:
直线方程的点斜式为:
最后标准的线性插值公式为:
将上式进一步展开:
这个公式的直观理解是:
y_0 乘以x_1 - x,表示靠近x_1 的影响
y_1 乘以x - x_0,表示靠近x_0 的影响
分母x_1 - x_0 进行归一化,使得结果保持在线性范围内
这表明,线性插值就是对两个已知值的加权平均,权重由x 在x_0 和x_1 之间的位置决定。
我们再给他变形一下,给出加权平均标准表达式:
如果x = x_0,那么y = y_0
如果x = x_1,那么y = y_1
如果x 在x_0 和x_1 之间,则y 在y_0 和y_1 之间
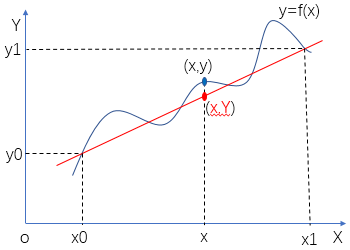
线性外推
线性插值(Interpolation): 只用于 x 在[x_0, x_1] 之间 的情况,计算范围在已知数据点之间,插值结果合理。
线性外推(Extrapolation):如果 x 超出 了[x_0, x_1] 的范围,我们仍然可以使用相同的公式计算 y 值,但这叫做 外推。
线性插值局限性
无法处理非线性数据,精度太差,特别是数据稀疏的时候,误差很大,而且不适用于噪声数据。
分段线性函数
如果有多个数据点,我们可以用分段线性函数,也就是多个线性插值拼接在一起
双线性插值
如果我们处理二维图像数据,可以使用双线性插值(Bilinear Interpolation),它在两个方向上分别进行线性插值,常用于图像缩放处理。相比于最近邻插值,双线性插值可以生成更平滑的结果。
原理
在图像缩放时,每个目标图像像素 (dstX, dstY) 需要找到其在原图像中的对应位置 (srcX, srcY),其计算公式如下:
(dstX, dstY) 是目标图像的像素坐标。
dstWidth, dstHeight 是目标图像的宽度和高度。
srcWidth, srcHeight 是原图像的宽度和高度。
(srcX, srcY) 是目标像素在原图中的对应位置。
如果(srcWidth/dstWidth) < 1,说明目标图比原图大(即放大图像),反之则是缩小图像。当 srcWidth/dstWidth = 1 时,相当于直接复制原图。由于srcX 和srcY 通常不是整数,需要通过插值计算该点的像素值。
插值计算过程
假设(x, y) 是目标图像的某个像素,对应到原图中的(srcX, srcY),即P 点。选择P 点周围最近的四个像素点( Q_{11}, Q_{12}, Q_{21}, Q_{22} ),如下图所示:
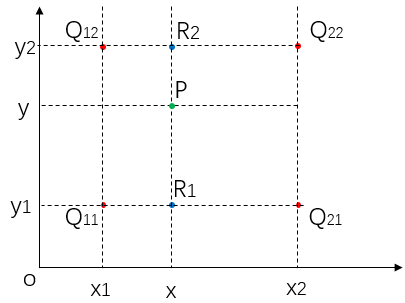
先在x 方向进行线性插值,计算R1 和R2:
再在y 方向进行线性插值,计算P 点的像素值:
经过化简,可以得到:
由于四个参考点的坐标间隔为 1,可以进一步简化为:
如果设x = i + u, y = j + v( i, j 为整数, u, v 为小数),公式可改写为:
这个公式表明, P 点的像素值是其四个最近邻点的加权平均值,权重由P 点相对四个邻点的位置决定。
示例:图像缩放
为了更直观地理解双线性插值的计算过程,我们以将图像放大两倍为例,并计算某个像素点的插值结果。
1. 计算原图像中的对应坐标
假设目标图像中某个像素的坐标为(5,4),要找到它在原图像中的对应位置,使用以下转换公式:
即该像素对应的原图坐标为(2.5, 2)。
2. 确定四个最近邻点
由于(2.5,2) 不是整数像素点,需要找到其周围最近的四个像素点Q_{11}、 Q_{12}、 Q_{21} 和Q_{22},即:
Q_{11} = (2,2)
Q_{12} = (2,3)
Q_{21} = (3,2)
Q_{22} = (3,3)
此时, srcX=2.5,可以分解为x = i + u,其中i = 2, u = 0.5 ; srcY = 2,即y = j + v,其中j = 2, v = 0。
3. 计算插值
根据四个最近邻点的 RGB 值:
应用双线性插值公式:
公式可简化为:
分别计算 R、G、B 分量:
R 分量: R = 0.5 \times 204 + 0.5 \times 102 = 102 + 51 = 153
G 分量: G = 0.5 \times 255 + 0.5 \times 255 = 127.5 + 127.5 = 255
B 分量: B = 0.5 \times 153 + 0.5 \times 153 = 76.5 + 76.5 = 153
最终,该像素的颜色为 RGB(153, 255, 153)。
4. 处理边界情况
如果srcX 或srcY 位于图像边界,可能会出现参考点超出图像范围的情况。例如,当某个点的四个最近邻点中有部分超出图像边界时,可以采用以下处理方式:
如果某个方向上超出范围,则使用相邻的边界点进行插值。
如果srcX 或srcY 是整数,意味着目标点恰好落在某个像素上,则直接取该像素的值。
最近邻插值
在学习 TensorFlow 处理图像缩放时,可能会遇到 tf.image.resize(image, (256,256), method=0) 这样的代码,其中 method=0 表示使用 双线性插值。本文主要介绍 method=1 的情况,即 最近邻插值法。
原理与应用
最近邻插值(Nearest Neighbor Interpolation)是一种最简单的插值方法,也称为 零阶插值。它的核心思想是:目标像素的值等于其在原图中最近像素的值,由于计算过程简单,最近邻插值在图像缩放中被广泛应用。然而,它的效果通常不如双线性插值,尤其是在放大图像时,可能会出现 像素块(块状效应)。
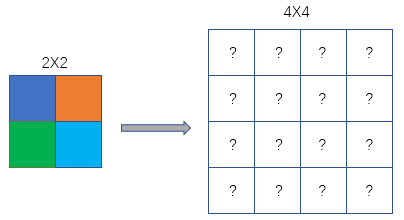
假设有一张 2×2 的小图,需要放大为 4×4,如何填充新增的像素呢?最近邻插值的策略是:
计算目标像素在原图中的对应坐标
找到最近的原图像素
复制该像素的值到目标像素
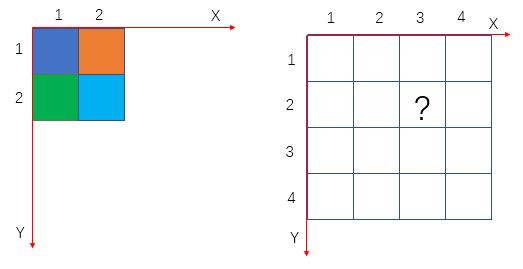
目标图像中 ? 位置的坐标为 (3,2),根据坐标转换公式计算:
计算得到的(srcX, srcY) = (1.5, 1),即该像素在原图中对应的位置在 (1.5 , 1) 。但像素坐标必须是整数,因此 四舍五入,得到(2,1),即原图中 (2,1) 的像素值。
通过类似的计算方式,可以得到整个放大后的 4×4 图像。
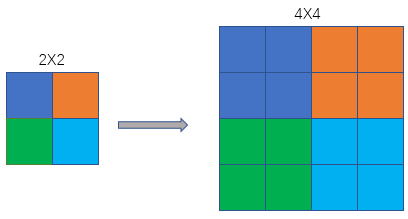
可以看到,最近邻插值直接复制了最近的像素,因此放大后的图像会有 块状边界,不像双线性插值那样平滑。
多项式插值
在插值问题中,我们希望通过一组已知数据点 (x_0, y_0), (x_1, y_1), \dots, (x_n, y_n),构造一个 n 阶多项式 f(x),使其满足:
这意味着我们找到的多项式 完全通过这些数据点。
下面介绍两种常见的多项式插值方法:Lagrange 插值法 和 Newton 插值法。事实上,这两种方法得到的插值多项式是等价的。
Lagrange 插值法
我们希望构造一个函数f(x),使其经过给定的点P_1(x_1, y_1), P_2(x_2, y_2), \dots, P_n(x_n, y_n)。为此,先设这些点在x 轴上的投影为P_i'(x_i, 0)。
接下来,我们考虑构造n 个函数f_1(x), f_2(x), \dots, f_n(x),让每个f_i(x) 仅在x_i 处取值y_i,而在其他插值点x_j(j \neq i) 处取值为0。也就是说,我们构造的基函数L_i(x) 应该具有插值性质:当x = x_i 时, L_i(x) = 1,而在其他x_j 处, L_i(x) = 0。
最终我们构造基函数形式如下:
将已知点P_i(x_i, y_i) 代入,得到系数:
因此, f_i(x) 可写为:
将所有插值基函数相加,即可得到最终的 Lagrange 插值多项式:
y_i 是已知数据点对应的纵坐标值。
举例
假设有一个数列:
我们希望构造一个基函数L_2(x),使其满足:
在x_2 处取值为 1,即L_2(x_2) = 1。
在x_1, x_3, x_4 处取值为 0,即:
为满足L_2(x) 在x_1, x_3, x_4 处为 0,我们构造如下多项式:
当x = x_1, x_3, x_4 时,它的值为 0,因此自动满足L_2(x_1) = L_2(x_3) = L_2(x_4) = 0。但这样还不够,因为我们需要L_2(x_2) = 1,但当前这个多项式在x_2 处的值并不是 1,而是: (x_2 - x_1)(x_2 - x_3)(x_2 - x_4),这是一个常数,我们需要通过 归一化 (Normalization) 让它变为 1。
为了确保L_2(x) 在x_2 处等于 1,我们除以它在x_2 处的取值:
这样:
当x = x_2 时,分子分母相等,因此L_2(x_2) = 1。
当x = x_1, x_3, x_4 时,分子有零因子,因此L_2(x) = 0。
现在,我们已经构造了一个在x_2 处等于 1,在其他插值点等于 0 的基函数L_2(x),但 Lagrange 插值的目标是满足:
因此,我们再乘以y_2,得到插值多项式的一部分:
同理,对于所有插值点x_i,我们可以构造:
最终,完整的 Lagrange 插值多项式为:
计算复杂度
朴素实现的时间复杂度: O(n^2)
计算每个f_i(x) 需要O(n),共有O(n) 项,因此总复杂度为O(n^2)。
优化方法:
通过 多项式快速插值 技术,可将时间复杂度降低至O(n \log^2 n)。
模坐标为连续整数的特殊情况
当已知的横坐标是连续整数时,我们可以在 O(n) 的时间内进行插值计算。
设要求n 次多项式f(x),且已知f(1), f(2), \dots, f(n+1),考虑代入 Lagrange 插值公式:
由于横坐标是连续整数,上式可以化简为:
为了进一步化简,我们将分子和分母分别拆开来看:
分子部分是一个连续整数的乘积,可以表示为:
分母部分是i - j 的连乘积,可以拆成两个阶乘相除的形式:
给出详细的推导过程
在 Lagrange 插值公式中,分母部分是:
也就是说,它是所有i - j 的连乘积,但不包括j = i 的情况,即:
可以看出,它分为两部分:
前半部分是1 到i-1 的阶乘,即(i-1)!。
后半部分是i+1 到n+1 的阶乘,即(n+1-i)!,且一共有(n+1-i) 个(-1),即(-1)^{n+1-i}。
综上,我们把分母整理成:
由此,我们可以得到最终的插值公式:
Newton 插值法
Newton 插值法是一种基于差分的插值方法,适用于动态插入新数据点的情况,能够在O(n) 时间内高效更新插值结果。
为了实现这一特性,我们构造插值多项式f(x):
其中, n_j(x) = \prod_{i=0}^{j-1} (x - x_i),称为 Newton 基(Newton basis)。
其更直观的完全展开形式如下:
a_j 是待求系数,如果求出系数a_j,就能确定插值多项式f(x)。这些系数可以通过 前向差商(forward divided differences)([y_0, y_1, \dots, y_j] )递归计算:
0 阶差商(即 j=0):
1 阶差商(即 j=1):
2 阶差商(即 j=2):
一般情况下的递推公式:
这些差商[y_0], [y_0, y_1], [y_0, y_1, y_2], \dots 依次对应a_0, a_1, a_2, \dots,因此插值多项式可以写成:
由此,Newton 插值多项式可表示为:
或者更紧凑地写成:
该方法的计算复杂度为O(n^2),但若使用合适的数据结构,可以优化至O(n)。
举例
假设我们有以下数据点:
(1) 计算前向差商
0 阶差商(即y 值):
1 阶差商:
2 阶差商:
(2) 构造插值多项式
根据 Newton 插值公式:
代入计算结果:
展开整理后:
等距插值的特殊情况
当插值点等距分布(即x_i = x_0 + ih, \quad i = 1, \dots, n),并令x = x_0 + sh,则 Newton 插值公式可化简为:
这个公式称为 Newton 前向差分公式,可以用于更高效地计算等距插值。
我们已知某个三次多项式:
并且给出f(1) 到f(6) 的值:
要求根据这些值确定多项式的系数a_0, a_1, a_2, a_3。
构造查分表
差分表的每一行表示对上一行的相邻元素求差,直到得到一个常数列为止。例如,这里我们计算:
其中,
第一列是x 值。
第二列是f(x) 的已知值。
第三列\Delta f 是相邻f(x) 的差,如5 - 1 = 4, \quad 14 - 5 = 9, \quad 30 - 14 = 16,依此类推。
第四列\Delta^2 f 是对\Delta f 继续求差,如9 - 4 = 5, \quad 16 - 9 = 7,依此类推。
第五列\Delta^3 f 是对\Delta^2 f 继续求差,如7 - 5 = 2, \quad 9 - 7 = 2,依此类推。
最终,我们得到\Delta^3 f 的值都是2,说明这个多项式的最高次项是三次的(因为三阶差分是常数)。
Newton 插值公式的推导
当x 取 连续整数(即x = 1,2,3,\dots)时,Newton 插值多项式可以写成:
其中:
\binom{k-1}{i-1} 是从k-1 取i-1 个的 组合数,用于表示多项式中的 Newton 基函数。
\sum_{j=1}^{i} (-1)^{i+j} \binom{i-1}{j-1} f(j) 这一项用于计算差分的首项系数。
这个公式可以理解为:
通过差分表计算f(x) 的 前 i 阶差分的首项。
计算k 处的插值值f(k),并利用组合数调整权重。
该方法的时间复杂度为O(n^2),因为计算差分表需要O(n^2) 的运算。
示例
我们用 插值公式 计算f(6),已知:
首先,计算前 i 阶差分的首项(差分表已经算出):
\Delta^0 f(1) = f(1) = 1
\Delta^1 f(1) = 4
\Delta^2 f(1) = 5
\Delta^3 f(1) = 2
Newton 插值多项式展开:
代入x = 6:
计算:
验证无误,与给定的f(6) = 91 相同。