飞机俯仰控制系统
编辑一.研究目的
为提高大仰角飞行状态下的飞机控制系统的稳态精度,为保持或者稳定飞行器的姿态角,需要对角度进行一定的控制,保证其稳定性
二.物理系统方程式
飞机总的方程式非常复杂,有六个非线性耦合微分方程,因此需对其进行解耦并线性化,分成横向和纵向方程。而此处的俯仰系统只由纵向动力学决定。
将设计一个自动驾驶仪(就是不同的控制器)来控制飞机俯仰角。飞机坐标轴建立与力如图所示。
对其中参数进行说明:
① X' Z' 都是地面坐标系,X Z 是机体坐标系,一个指向机头,一个指向机腹,原点为飞机质心
② θ 为俯仰角(姿态角) α 为气动角 δ 为升降舵偏转角
③ v 是速度方向,构成了风轴系
为了简化问题,我们假设①现在的推力 阻力在x轴上平衡,重力与升力在Y轴上平衡。与此同时,假设②俯仰角θ的变化并不会改变飞机速度的变化。由此可以得到纵向运动方程如下:
可见,输入是 δ,输出是 θ
三.寻找传递函数并建立状态空间表达式
1.传递函数的求得
将上述纵向运动方程简化
将其进行拉普拉斯变换,使用单位阶跃输入 R(s) = 1/s 得
阶跃信号用于模拟突然变化的输入,例如飞机需要快速响应新的姿态角设定
不难得到传递函数
2.状态空间方程
状态空间形式便于在多输入多输出(MIMO)系统中统一表示动态方程,因此由上述公式写成矩阵形式有
四.系统分析
1.设计要求
输入信号为阶跃信号,要求得到的波形性能指标如下:
俯仰角的超调量小于10%
上升时间小于2s
稳定时间小于10s
稳态误差小于2%
2.开环传函系统分析
%% 定义传递函数和开环系统分析
% 定义传递函数
s = tf('s');
P_pitch = (1.151*s + 0.1774)/(s^3 + 0.739*s^2 + 0.921*s);
% 绘制开环系统的阶跃响应
t = 0:0.01:10; % 时间向量
figure;
step(P_pitch, t);
ylabel('俯仰角 (度)');
xlabel('时间 (秒)');
title('开环系统的阶跃响应');
grid on; % 增加网格便于观察
set(gca, 'FontSize', 12); % 增大字体,便于阅读
% 检查传递函数的极点
disp('开环系统的极点为:');
open_loop_poles = pole(P_pitch);
disp(open_loop_poles);得到三个极点与开传函图像:
0.0000 + 0.0000i
-0.3695 + 0.8857i
-0.3695 - 0.8857i
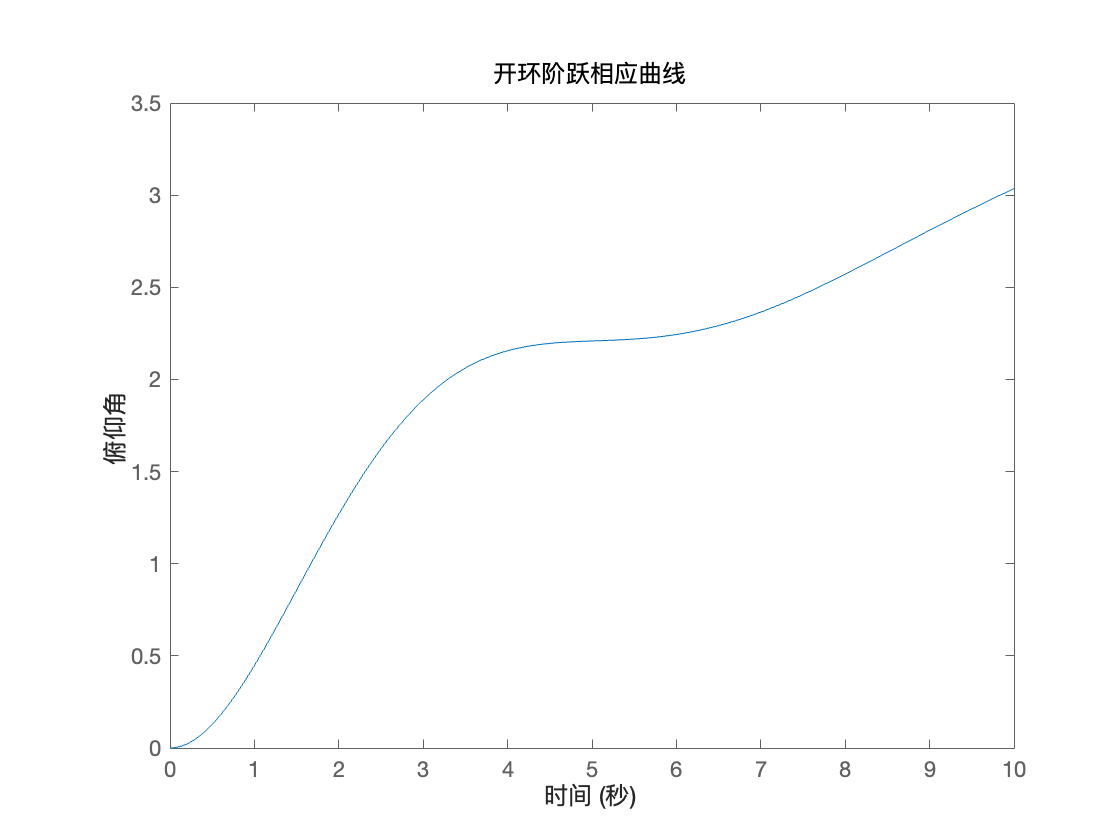
要对其进行修正,而极点也表明了,一个极点在虚轴上,其他两个极点在复数域s的左半平面。这个虚轴上的极点表示其相应波形并不会无限上升,但即使如此,由于虚轴极点的特性,给定输入时,依然有可能无限上升。即虚轴极点导致系统对阶跃输入响应呈现无界增长,这是不稳定开环系统的典型特征,在此种特殊情况下,其极点像个积分器,当给定阶跃输入时,对其常数进行积分会导致输出无穷大。
3.闭环传递函数性能分析
显然开环不能满足,加入反馈模块。
%% 闭环系统分析
% 定义闭环系统(单位反馈)
sys_cl = feedback(P_pitch, 1);
% 绘制闭环系统的阶跃响应
t = 0:0.01:60; % 使用更长时间范围分析系统收敛特性
figure;
step(sys_cl, t);
ylabel('俯仰角 (度)');
xlabel('时间 (秒)');
title('闭环系统的阶跃响应');
grid on;
set(gca, 'FontSize', 12);
% 检查闭环系统的极点
disp('闭环系统的极点为:');
closed_loop_poles = pole(sys_cl);
disp(closed_loop_poles);闭环传递函数
在阶跃响应下的波形图:
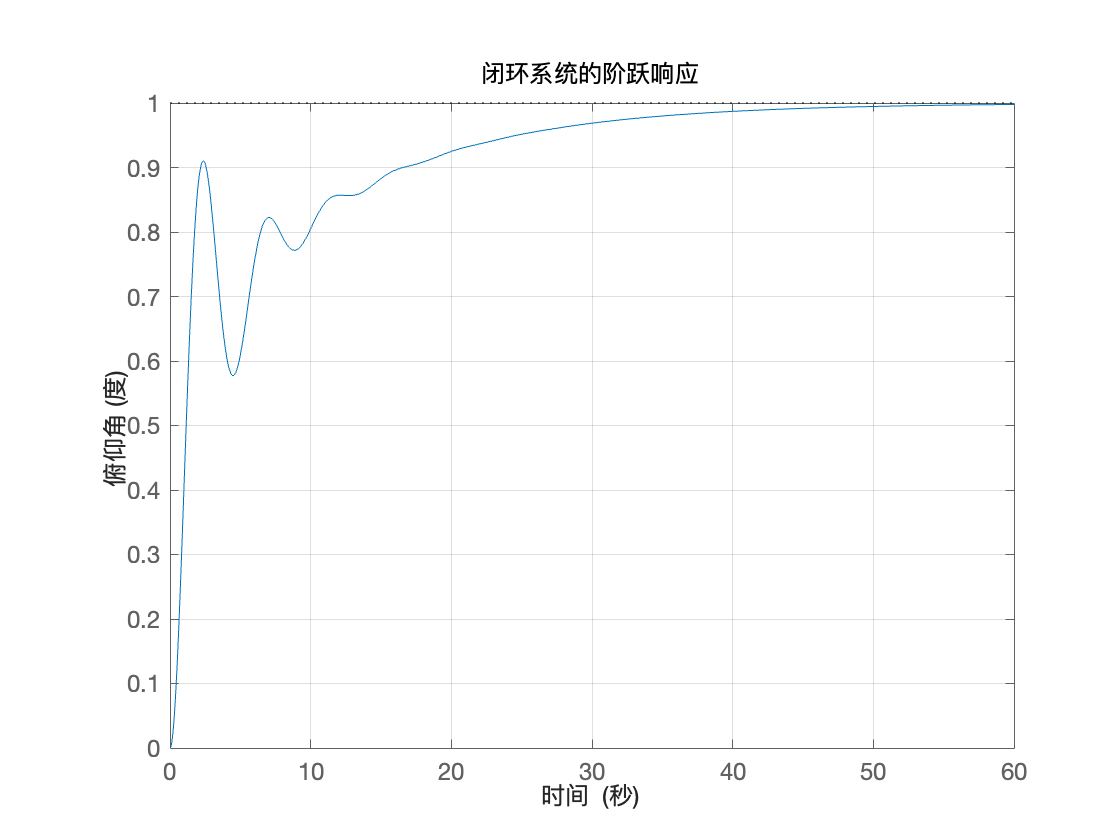
由图可见,闭环系统仍然不满足要求,但稳态误差e近乎为0,且无超调量
(1)继续对传递函数的极点与零点进行分析
% 查看闭环系统的极点
disp('闭环传递函数的极点为:');
pole(sys_cl)不难看出,其闭环传函系统是稳定的,因为所有极点都具有负实部,尽管都位于左半平面,但复共轭极点的虚部较大,导致系统呈现较明显的振荡特性。此传递函数是三阶系统,由于往常都是使用标准的无阻尼且无零点的二阶系统,因此在本例中不可以依赖零极点关系。不如将输出转换回时域,用系统响应时间函数来了解零极点如何影响系统。
(2) 闭环传递函数形式为 Y(s)/R(s), 可得 Y(s) = \text{传递函数} \cdot R(s)
再将得到的 Y(s) 进行分解因式,部分分数展开用于将高阶系统的传递函数分解为一阶和二阶子系统的叠加,便于理解其动态响应,使用命令 zpk 进行分解。
%% 分解闭环系统传递函数
% 定义阶跃输入 R(s) = 1/s
R = 1/s;
% 分解闭环输出 Y(s)
Y = zpk(sys_cl * R);
disp('闭环系统输出传递函数的零极点增益形式:');
disp(Y);可以看出,其极点分布为,原点,实极的一阶项,共轭复极的二阶项。再将其因式分解成如下形式
(3)现在就开始求ABCD,可手动计算,或用命令计算,使用residue命令
% 部分分数展开
[r, p, k] = residue([1.151 0.1774], [1 0.739 2.072 0.1774 0]);
disp('部分分数展开的残差 (零点分布):');
disp(r);
disp('部分分数展开的极点:');
disp(p);
disp('多项式余项:');
disp(k);
零点
极点
r 包含部分分数展开的残差,即 A, B;p 包含系统的极点,极点的阶次对应 r 中残基的阶次;k 由于通常分子多项式比分母多项式小,一般为空,因此 A = 1, B = -0.0881
(4)接下来再求CD,其求法为让复共轭极点项分解成单项表达式来确定
% 提取复共轭极点部分
[num, den] = residue(r(1:2), p(1:2), k);
disp('复共轭极点部分的分子与分母:');
disp('分子:');
disp(num);
disp('分母:');
disp(den);可得
C = -0.5605, D = -0.4036
(5)至此,ABCD全得到了,进行逆变换求解
%% 求解闭环系统的时域响应
syms s t
F = 1/s - 0.881/(s + 0.08805) - (0.5605*s + 0.4036)/(s^2 + 0.6509*s + 2.015);
y_t = ilaplace(F);
disp('闭环系统的时域响应表达式:');
disp(vpa(y_t, 4)); % 显示高精度表达式(6)得到了 y(t)
每个项应该对应传函极点,而极点的实部又描述了其指数的增长或衰减,虚部对应其振荡频率
至此可以了解拉普拉斯域中零极点如何影响时域。
(7)将时域进行画图,和之前应该对应
%% 绘制闭环系统的时域响应曲线
% 定义时间向量
t3 = 0:0.1:70;
% 时域响应的计算
yy = 1 - (1121*exp(-(6509*t3)/20000).*(cos((763632919^(1/2)*t3)/20000) + ...
(8847411*763632919^(1/2)*sin((763632919^(1/2)*t3)/20000))/856032502199))/2000 - ...
(881*exp(-(1761*t3)/20000))/1000;
% 绘制时域响应曲线
figure;
plot(t3, yy, 'LineWidth', 1.5); % 增加曲线宽度
xlabel('时间 (秒)');
ylabel('俯仰角 (度)');
title('闭环系统的时域响应曲线');
grid on;
set(gca, 'FontSize', 12);
% 标注响应特性
text(15, 0.8, '稳态响应近似为1', 'FontSize', 12, 'Color', 'red');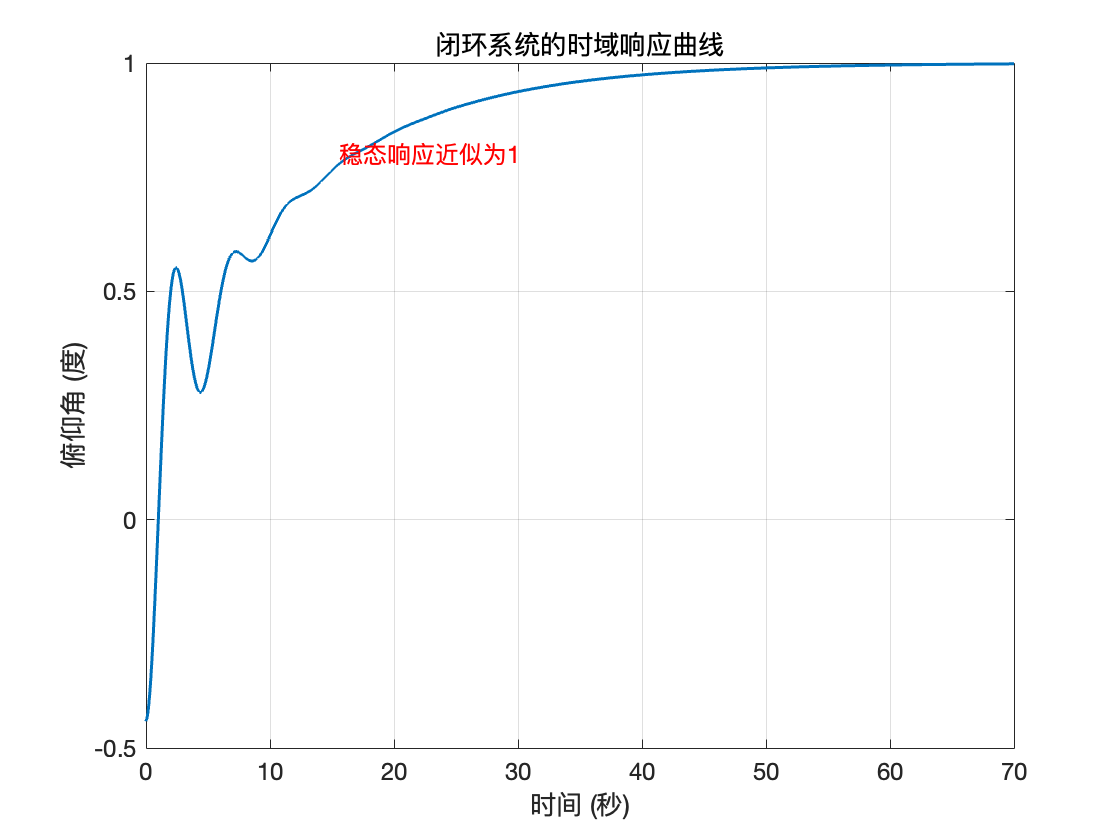
(8)至此表明闭环也不能满足要求,接下来设计一些其他的控制器来完成目标性能
五.控制方法与结果分析
1.根轨迹法
闭环根轨迹增益=开环前向通路根轨迹增益(单位反馈)
闭环传递函数的零点分别为开传函的零点+反馈回路的极点,若反馈回路为1,则就是开传函的零点。即闭环零点=开环零点
闭环极点与开环零点,开环极点以及根轨迹增益K均有关
对根轨迹做出一些解释说明
根轨迹设计的主要思想是 有很多可能的闭环极点位置,当处于某个位置的时候,去预测闭环输出响应。因此,通过增加零点或者极点,就可以修改根轨迹,使得极点可以处于新根轨迹上新的位置,从而可以实现所需要的闭环响应。而这个不断选择的位置其实本质就是Kp值的大小。
增加开环极点对根轨迹的影响如下:开环极点会改变根轨迹在实轴上的分布,并改变渐近线的条数+倾角+截距,改变根轨迹分支数,根轨迹会向右偏移。在这种情况下,不利于稳定性与动态性能,并且所增加的开环极点越靠近虚轴,影响就越大
增加开环零点对根轨迹的影响如下:开环零点同样会改变根轨迹在实轴上的分布,并改变渐近线的条数+倾角+截距,如果开环零点与开环极点相距很近,或者近乎重合,那么两者可以相互抵消。因此通常加入零点来抵消不利的开环极点,引入开环零点后根轨迹会向左偏移,会提高稳定性,改善动态性能,同样,开环零点越靠近虚轴,影响就越大
(1)先找到开环传递函数根轨迹图
%% 根轨迹法 - 开环根轨迹设计
% 定义传递函数
s = tf('s');
P_pitch = (1.151*s + 0.1774)/(s^3 + 0.739*s^2 + 0.921*s);
% 打开控制系统设计器进行根轨迹分析
controlSystemDesigner('rlocus', P_pitch);因此打开了控制系统设计器窗口,其中的控制器 C(s)=K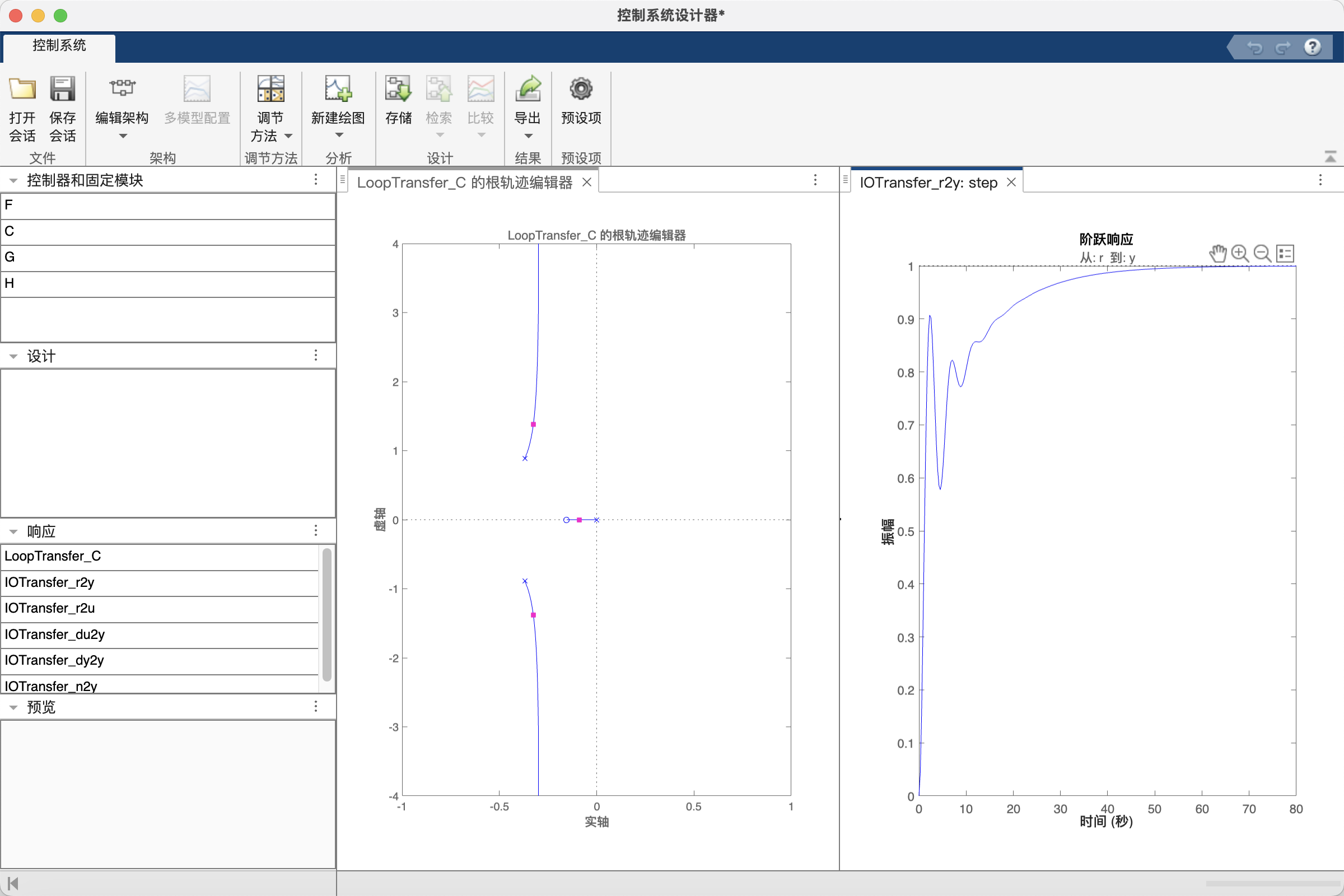
(2)打开左上角'编辑架构',可修改回路模型,我们就用最简单的反馈就行
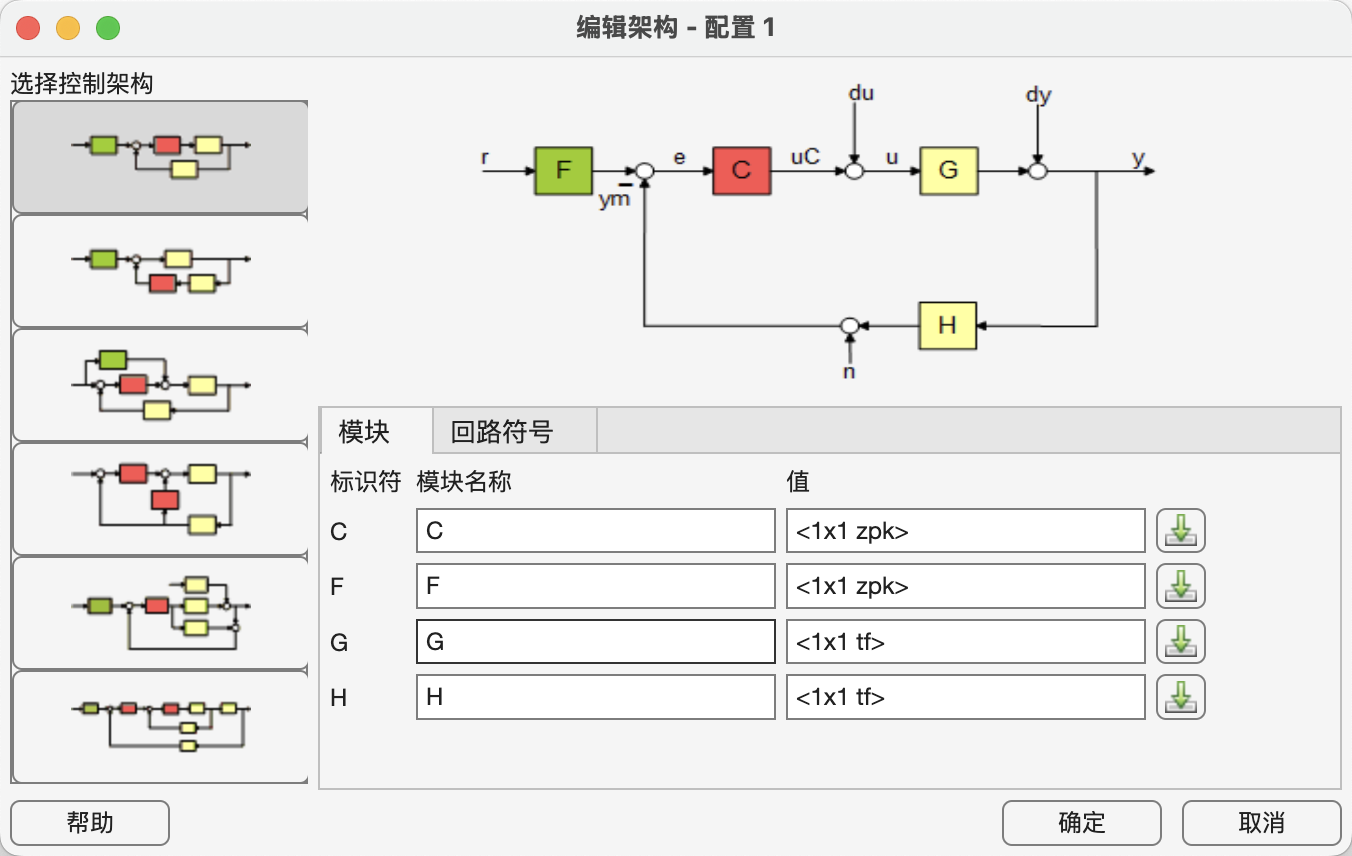
再回到主页面,在根轨迹编辑器的图中右键,非常隐蔽,不然我赌你肯定找不到, 然后可以调参数(例如调F)(在编辑补偿器里) ,这里我们在设计需求中新建设计参数的范围
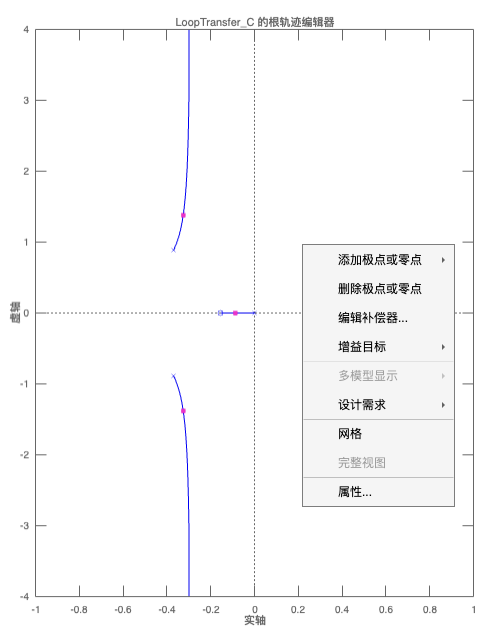
对各项性能指标提出要求,其中上升时间不能直接调节,只能通过调节固有频率的方式间接改变,其关系如下
根据要求新建并调调其他参数
(3)参数调节完毕后,得到下图
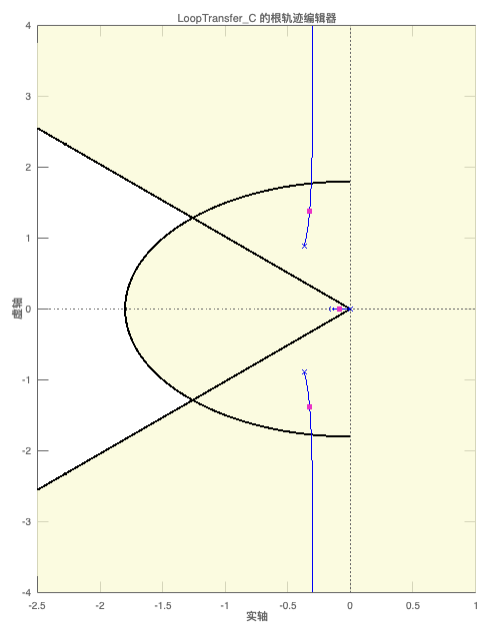
极点位置与瞬态性能有关,不如先把满足要求的参数调好,得到满足要求的区域。上面得到的非阴影区域就是闭环极点的最终所需区域。
换句话讲,以原点为中心的两条射线代表超调要求,射线与负实轴构成的角度越小,则超调量越小。在s=-0.4处有一条垂直线,表示了建立时间的要求,闭环极点越靠近左侧,建立时间就越短。上升时间对应于以原点为中心的圆,其半径就是固有频率的值。
不难看出,开传函的三个分支都没有进入非阴影区,无法通过改变控制器的比例增益K来讲闭环传函极点放在非阴影区,因此考虑尝试用带极点/零点的动态补偿器
超前补偿器
(4)要想将根轨迹在复平面上往左移动,采用超前补偿器,传函如下
其中零点的幅度小于极点的幅度(z < p),即零点在复平面中更加靠近虚轴。
(5)现在开始选择超前补偿器的传递函数
点击右上角预设项
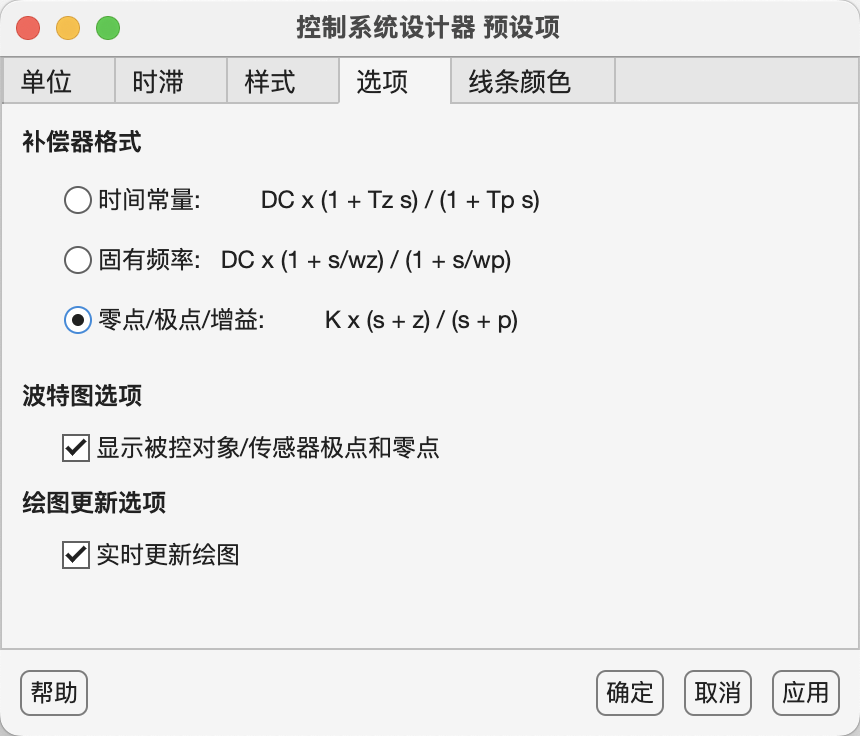
(6)随后进入编辑器的参数设置,不如把零点放到 Z=-0.9 (就是上升时间对应的固有频率所形成的圆的左半面的实轴上),可以保证随着后面K的增加,零点根轨迹一定在非阴影范围内,并且将极点放在与零点更远的地方 p=-3 (下面图应该极点为-3)。跟着下面这个参数添加一个超前零极点并配置好对应数值就行
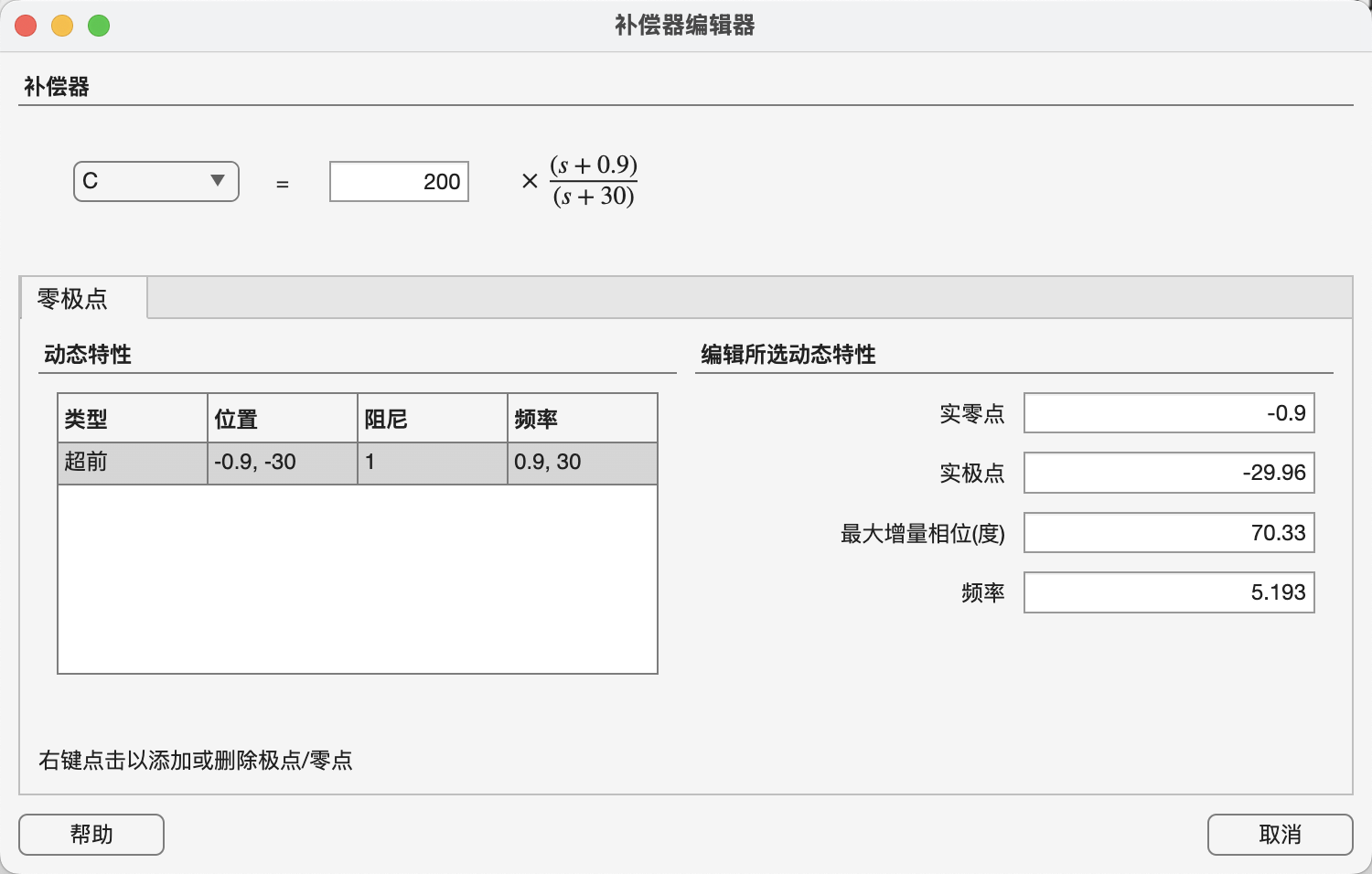
(7)随后可以看到新的根轨迹图像,零极点是可以拖动的
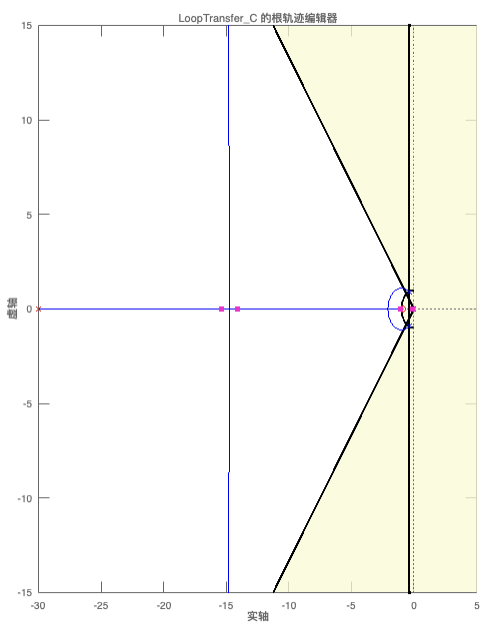
(8)右键属性中可以调节XY范围,现在放大观看右边的零极点情况
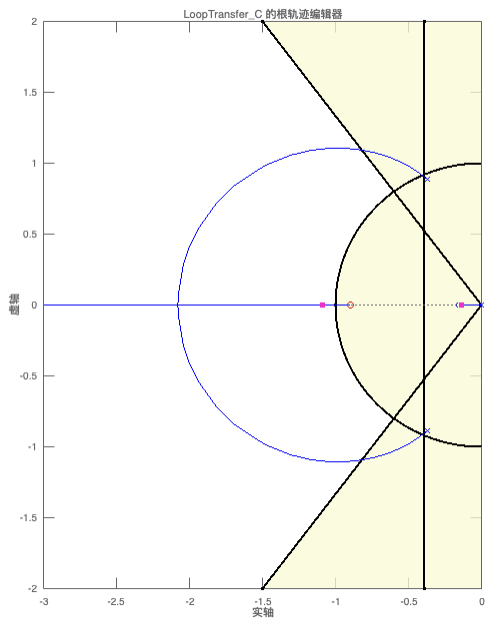
不难看出,零极点的三条线分支在规定范围内,唯独有一个不在范围内,此极点比其他极点慢,但其响应被隔得非常近的那个零点所抵消。环路增益K 越大,闭环极点就越靠近闭环零点,闭环极点所产生的影响就越小。最左边的闭环极点对系统的响应程度最小,因为它比其他极点快得多
当前极点位置所得到的环路增益K 可以在左下方得出。
(10)现在重新查看闭环阶跃响应曲线图,右键参数设置里可以勾选上升时间、稳定时间等虚线。
我们的K = 200,可见所有极点仍在实轴上,也就是没有超调,最终误差e=0,满足设计条件
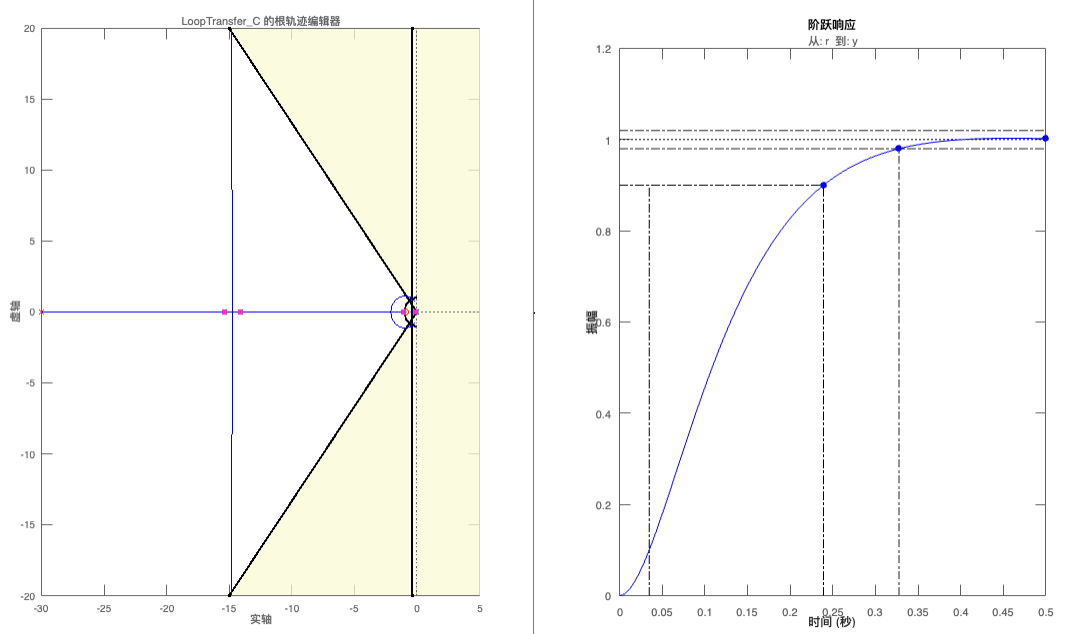
(11)总结:
至此,采用根轨迹法的控制器设计完毕,从最初的C(s)=K 不能满足要求,到增加超前环节,到最后调节K 值来使闭环极点移动,以使得阶跃响应曲线达到了良好的结果。其实,根轨迹中采用超前补偿器的根本核心就在于在闭环中增加了一项超前补偿器的传函,加入这个环节后可以改变根轨迹,让更稳定的点在根轨迹上。
换句话说,当我们希望闭环的根往左移动(更稳定时),引入超前补偿即可
为什么叫超前补偿器?因为其相角裕度是正的,加入到系统相位上可以使相角增大,就是使系统相位裕度增大,稳定性就大大增强。因为相角超前,叫超前补偿器
2.频域分析法
频率设计的主要思想是利用开环传递函数的Bode图来估计闭环响应,如果向系统添加控制器,会改变开环伯德图,进而改变闭环输出响应,频域分析法直观地展示了系统的增益裕度、相位裕度,以及响应速度与稳定性的关系,为后续设计补偿器提供了依据
(1)在之前分析闭环传递函数的时候,已经分析得到有三个极点,一个零点,且闭环系统是稳定的。现在其稳定性再由开环频率响应来确定,采用margin命令来生成伯德图,并注释增益裕度与相位裕度
%% 频域分析法 - Bode图与补偿器设计
% 定义传递函数
s = tf('s');
P_pitch = (1.151*s + 0.1774)/(s^3 + 0.739*s^2 + 0.921*s);
% 初始开环系统的Bode图与裕度分析
figure;
margin(P_pitch);
grid on;
title('开环系统的Bode图 (未补偿)');
xlabel('频率 (rad/s)');
ylabel('幅度与相位');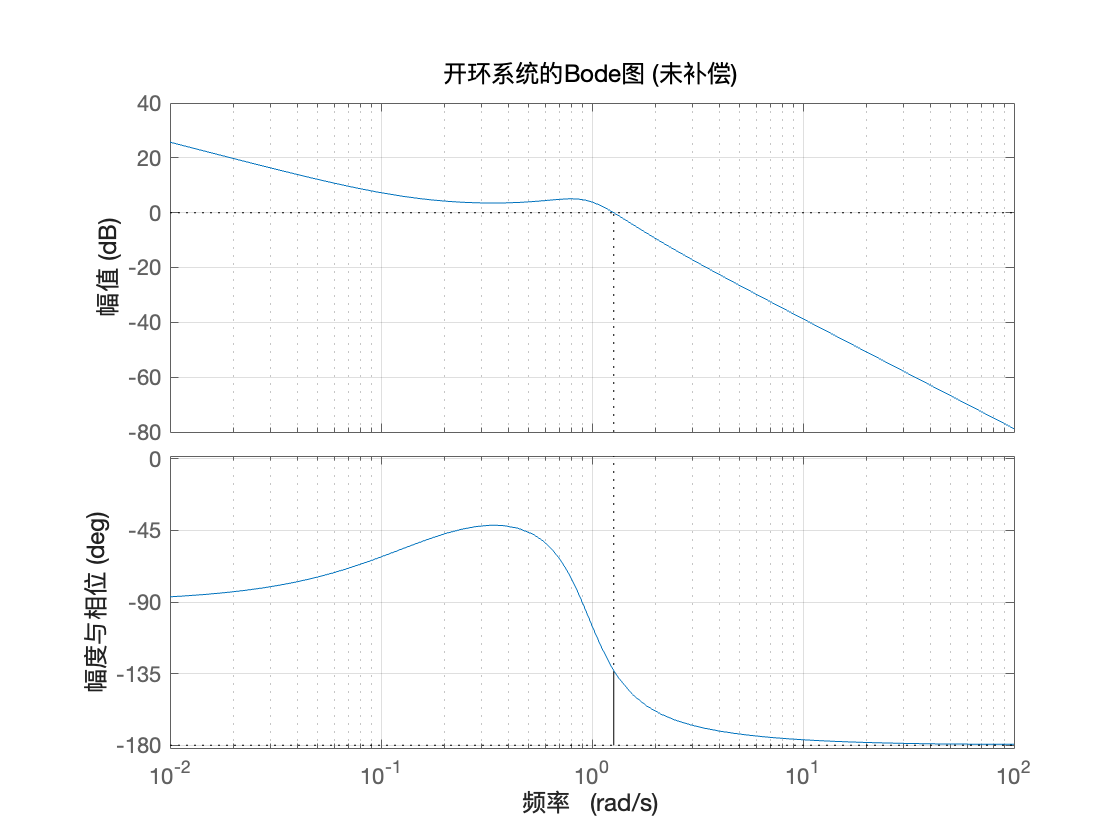
可见,增益裕度为Inf,相位裕度位46.9,都为正,说明系统稳定(目前的增益裕度是无限的,这表明该系统是稳健的,具有最小的超调,相位裕度为 46.9^\circ 意味着系统有一定的稳定余量,但不能保证快速响应)。所以满足要求?
(2)重新回到上面求得的阶跃响应图
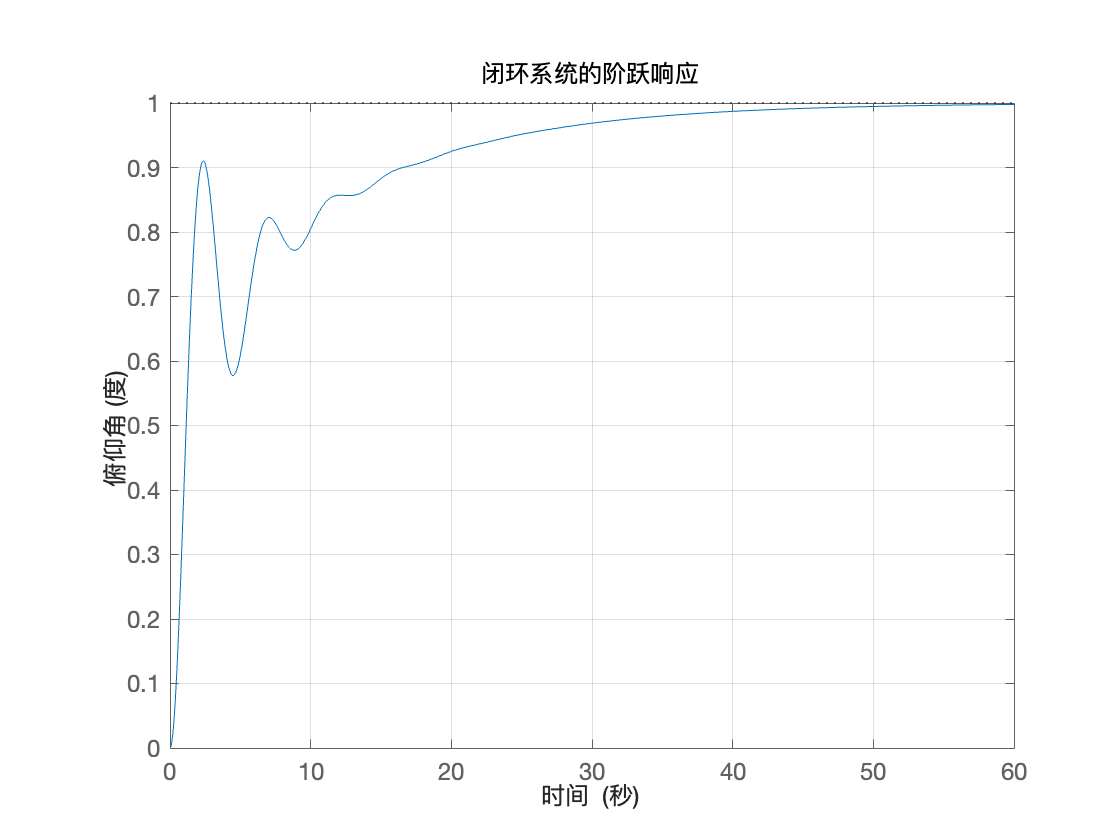
我们通过分析闭环的阶跃响应发现系统是稳定的,只是稳定时间等等均不满足指标,想加快系统响应,就容易导致过冲问题,因此想再次使用补偿器来重塑开环系统的伯德图(开环系统的伯德图表示了闭环系统的行为)(增益交叉频率与闭环响应速度呈正相关,而相位裕度与过冲成反比),采用一个补偿器来加快增益交叉频率且增加相位裕度。因此也采用超前补偿器。其核心目的是优化系统的响应速度和阻尼特性。通过调整零点和极点的位置,它既可以提升增益交叉频率(加快响应速度),又能增加相位裕度(减小过冲)
超前补偿器
(3)超前补偿器为系统增加了正相位,这样可以增加相位裕度,从而增加阻尼。与此同时,它还可以在高频率下增加开环频率响应的幅度,进而增强增益交叉频率和整体速度(稳定时间降低)。
其传递函数一般形式如下:
(4)通常将K 设置为满足稳态误差的要求,而由于系统是Ⅰ型的,因此不管任何K 值,阶跃输入的稳态误差都是0。增大K 值会使幅度图往上移动。经选择后,令K=10
% 设置增益K并观察频域响应
K = 10; % 增益设置
figure;
margin(K * P_pitch);
grid on;
title('加增益后的Bode图 (K=10)');
xlabel('频率 ');
ylabel('幅度与相位');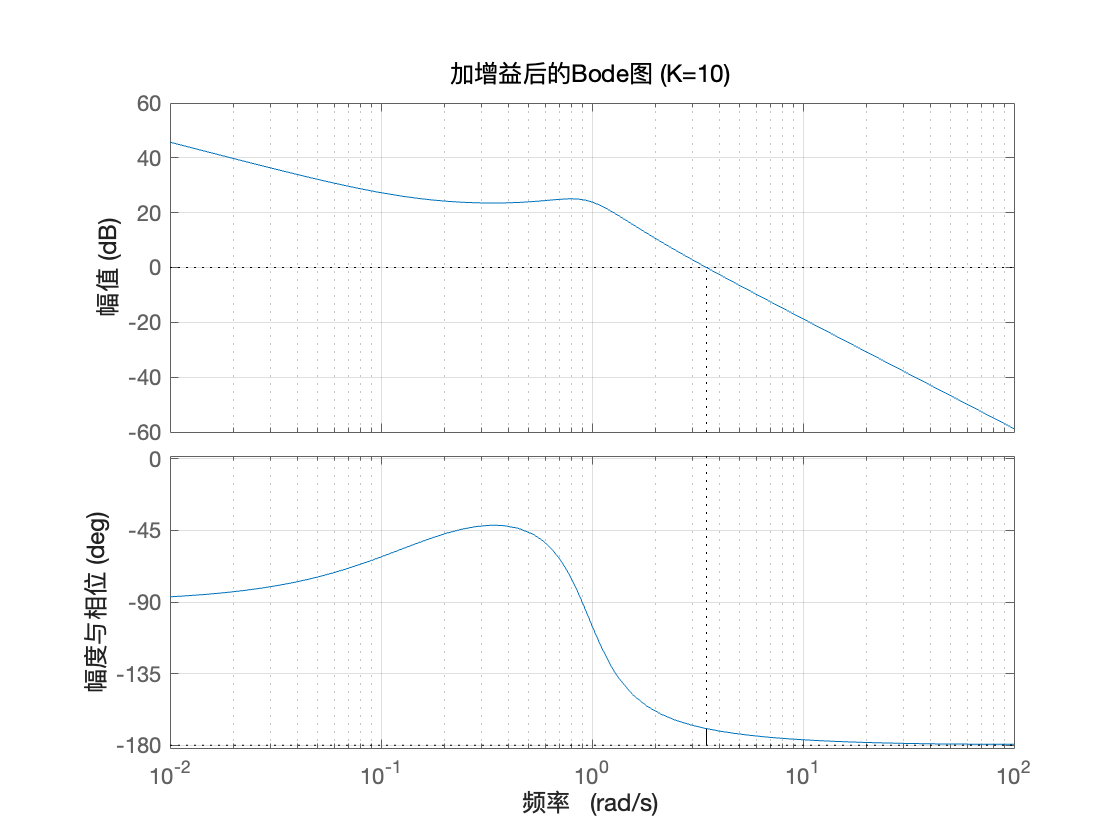
可见,我们增加了系统的幅度,并且提高了增益交叉频率,可得出的是随着K的增加,相位裕度也减小了,意味着超调量增加了,这是我们不希望的,但超前补偿器是可以增加系统的阻尼的,也就是说有办法来减小超调量
(5) 于是继续寻找 \alpha,其定义为零点与极点的比值。零点与极点间隔距离越大,相位的凸点就越大,其中单个零极对可以最大增加相位为 90^\circ。最大相位与 \alpha 的关系如下:
同时我们也知道标准欠阻尼二阶系统的时间响应与频率响应之间的关系
通常阻尼比\zeta 近似小于 0.6 或 0.7。
(6) 尽管之前的系统并不是标准的二阶系统,但仍可以用以上关系进行设计。由于超调量要求小于 10%,也就是说,阻尼比\zeta 要大于 0.59(关系图可以在网上找到),因此相位裕度需要大于59^\circ。根据超调量与阻尼比的关系,可以先从目标超调量反推出阻尼比,再通过近似公式计算所需的相位裕度
当前相位裕度为 10.4^\circ,因此再增加 50^\circ 就足够了。由于超前补偿器会额外增加频率响应的幅度,因此需要添加超过 50^\circ 的相位超前。最终我们选定 55^\circ 的相位超前为目标。
(7)然后计算 \alpha
(8)因此 \alpha 必须小于0.1,再根据下面关系式计算出超前补偿器所造成的幅度增加量
(9) 在之前的图中可以看出,穿过幅值 = 0 那条线的交叉频率 \omega_c = 3.49,穿过幅值 = -10 \, \text{dB} 的频率为 6.1 \, \text{rad/dec}。由此不难想到,加入超前补偿器的 \alpha 后,其交叉频率会变为 6.1。然后我们再利用这个新交叉频率值来计算 T,目的是使最大相位裕量增加到最大。因为参数 \alpha 控制了零点和极点之间的距离,从而决定了补偿器的相位峰值大小以及频率范围。
(10) 由此,超前补偿器的三个变量值全部得到:K = 10, \alpha = 0.1,T = 0.52。将这些值通过编程应用于开环传递函数,观察超前补偿器对系统频率响应的影响。
% 定义超前补偿器参数
alpha = 0.1; % 零点与极点的比值
T = 0.52; % 时间常数
% 超前补偿器传递函数
C_lead = K * (T*s + 1) / (alpha*T*s + 1);
% 补偿后的开环传递函数
P_lead = C_lead * P_pitch;
% 绘制补偿后的Bode图
figure;
margin(P_lead);
grid on;
title('加入超前补偿器后的Bode图');
xlabel('频率 ');
ylabel('幅度与相位');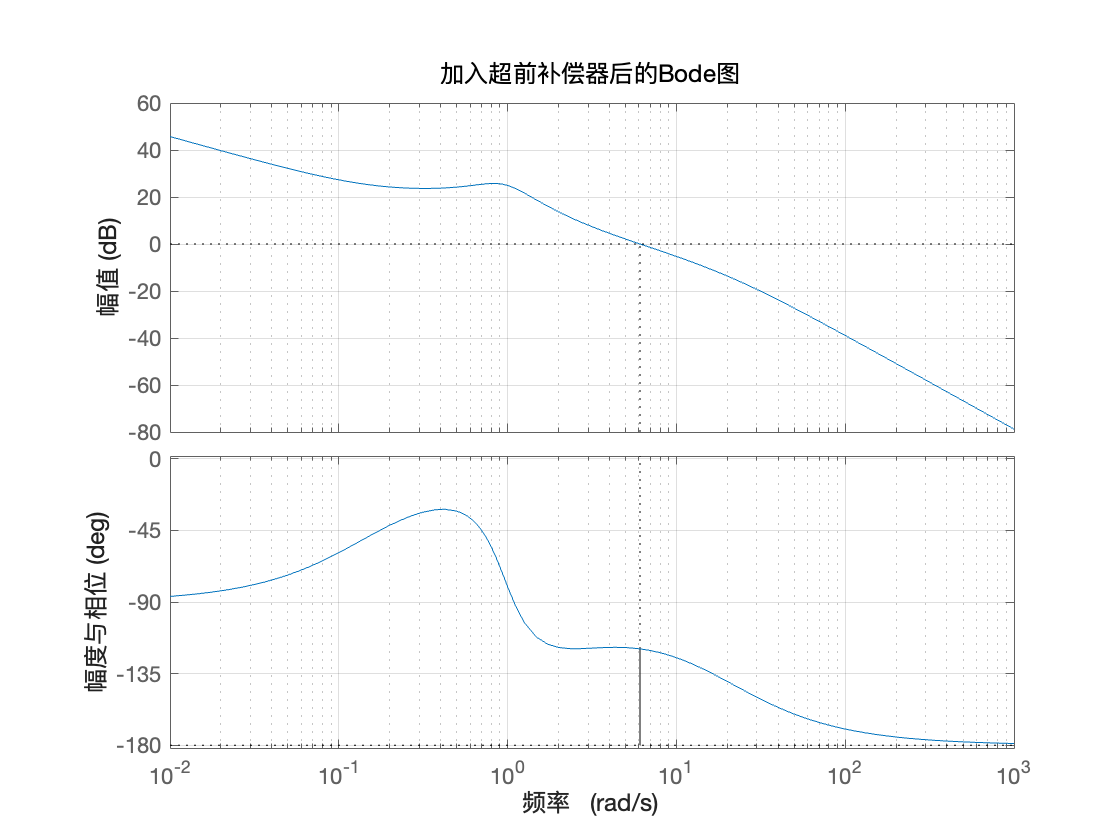
可见相位裕度和交叉频率都提高了
(11)接下来再看闭环阶跃响应
% 补偿后的闭环系统
sys_cl_lead = feedback(P_lead, 1);
% 绘制闭环阶跃响应
figure;
step(sys_cl_lead, 0:0.01:10);
grid on;
title('超前补偿器设计的闭环阶跃响应');
ylabel('俯仰角 (度)');
xlabel('时间 (秒)');
% 获取闭环系统的性能指标
disp('超前补偿器设计后的闭环系统性能:');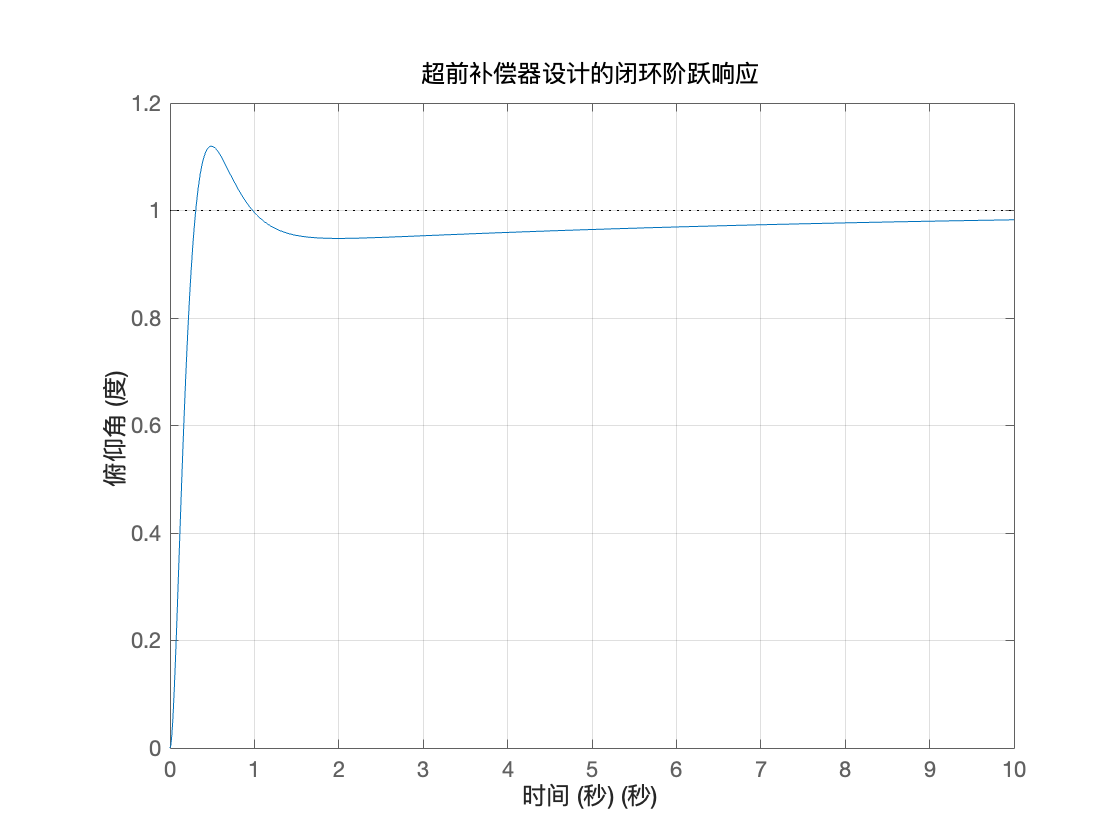
从图上很难细致的看出超调量等参数,因此采用stepinfo命令
stepinfo(sys_cl_lead);(12) 得到参数后,计算发现超调量还是略大了一些,此时重新调整取 \alpha = 0.04,结果改善了许多:
(13) 综上,超前补偿器设置完毕 ( \alpha = 0.04 )
超前补偿器的传递函数为:
总结:
原闭环系统稳定,但一定不满足要求的调节,通过频域分析确定初始系统的缺陷后,利用超前补偿器增加相位裕度和增益交叉频率,从而优化了响应速度和稳定性。这种设计方法强调频域与时域性能的结合,通过不断调整 \alpha 和T 实现精确的动态控制。换句话说频率分析法也只是看看它稳不稳定罢了,至于要让他满足要求,还得是设计各种前馈器,让他的整体传递函数变化,从而改变伯德图里的相位裕度以及交叉频率,增加相位裕度可以提高阻尼系数,增加交叉频率可以减小稳定时间。单独的增加K 可以增加交叉频率,但有缺陷,因此又引入了 \alpha 与T 来调节相位裕度与超调量。
比较难的地方在于 \alpha 的选择,选 \alpha 一定就要先找要增加多少相位?也就是目标相位 - 原始相位(带K),目标相位怎么找?用超调量找阻尼比再找相位(图标关系),于是可以得出,根据要求的超调量就可以找到 \alpha,其T 值水到渠成地就得到了,因此整个超前补偿器就设计完毕了。但仍需要不断观察伯德图与输出响应曲线来对比不同之处,并判断是否的确满足系统要求。
3.状态空间法
(1)前面已经得到过状态空间形式的动力学方程
上面等式与一般的线性状态空间形式匹配
(2)因此将采用状态空间控制器来设计系统,来放置闭环极点
要想设计状态空间控制器,首先要看能控性能观性。能控性对应了我们可以将闭环极点放置在s平面的任意位置,给出能控性矩阵
(3) 其中 n 对应状态变量的数量。由于我们的矩阵为 3 \times 3 ,因此矩阵的秩 \text{rank} 也必须为 3(满秩)。为了验证这一点,可以使用命令来查看矩阵的秩。
%% 连续状态空间法 - 能控性与极点布置
% 定义连续状态空间模型
A = [-0.313 56.7 0; -0.0139 -0.426 0; 0 56.7 0];
B = [0.232; 0.0203; 0];
C = [0 0 1];
D = [0];
% 检查系统能控性
co = ctrb(A, B); % 能控性矩阵
Controllability = rank(co);
disp(['连续系统能控性: Rank = ', num2str(Controllability)]);其中co为:
得到结果连续系统能控性: Rank = 3,证明矩阵满秩,完全可控。能观性略
通过极点布置来进行控制设计
(4)全状态反馈控制系统原理图如下(ABC就是表达式里的值,这里D=0)
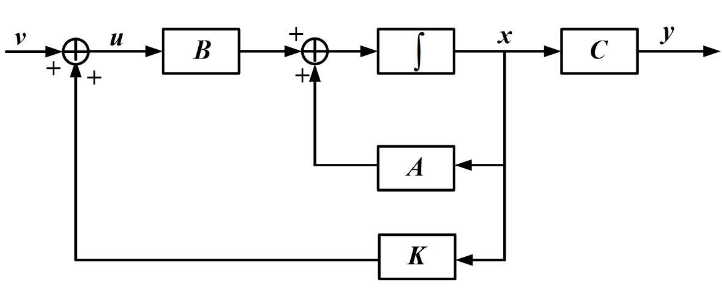
其中 K 为增益矩阵, \mathbf{x} = [ \alpha , q , \theta ]^\top 为状态向量, \theta_{\text{des}} 为参考信号 ( r ), \delta = \theta_{\text{des}} - K \mathbf{x} 为控制输入 ( u ), \theta 为输出 ( y )
(5) 由于新的 \delta = \theta_{\text{des}} - K \mathbf{x} ,将其代入到原状态方程中,得到新状态方程如下:
因此,矩阵 A - BK 确定了系统的闭环动力学,其行列式 \det(sI - (A - BK)) 的根是系统的闭环极点。由于该行列式是三阶的,因此可以任意放置的极点数量为三个。再加上系统是完全能控的,因此极点的位置可以随意配置。
控制系统的性能主要取决于系统的极点在根平面上的分布。可以按照设计意图调整的参数是反馈增益矩阵 K。经典控制理论中的根轨迹法就是一种极点配置方法,其核心目标是通过各种手段重新配置开环系统的极点与零点。
需要注意的是,此反馈定律假定矢量 \mathbf{x} 中的所有状态变量均已被测量,否则需要设计一个观察器来估计状态变量。
注意:实际上并不是只有这一种新的状态方程,也可以引入一个状态观测器 G ,然后以 C 来算,不过很麻烦。举例如下
状态观测器公式:
反馈控制率公式:
根据系统性能指标的公式:
超调量:
调整时间:
系统闭环特征方程:
阻尼比:
自然频率:
超调量:
调整时间:
(6)因此有三个可以任意放置位置的极点,可问题是放在哪里?如果有标准的一阶或者二阶系统,那么极点的位置与阶跃响应的特性有直接的关系,利用这些关系可以得到极点的位置。但是如果是高阶系统,可以将高阶极点放置在复平面中比主导极点偏左 5-10 倍的位置(由于太左,对瞬态响应的影响就忽略不计了)。但是这样也有两点局限性:
其一是 难以解决零点的问题;
其二是 工作量可能大。
由此可见,这种放置极点的方法不行。
(7)因此,为了得到反馈增益矩阵 K ,将使用 LQR(线性二次调节器)来生成最佳增益矩阵 K 。这样就不必计算要将极点放在哪个特定位置。若要使用 LQR,需要定义两个参数:状态成本加权矩阵 Q 和控制权重矩阵 R 。为图简单,选择 R = 1 , Q = p C^\top C 。在这种情况下, \theta 是输出中唯一的状态变量,而加权因子 p 将被更新以修改阶跃响应。对于 R ,由于只有一个输入,因此它是标量。
(8)LQR 参数全了,接下来得到反馈控制矩阵 K ,先令加权因子 p = 2 。
% 定义LQR权重矩阵
p = 50; % 状态加权因子
Q = p * C' * C; % 状态成本加权矩阵
R = 1; % 控制权重矩阵
% 求解状态反馈增益矩阵K
[K] = lqr(A, B, Q, R);
disp('LQR设计的反馈增益矩阵K:');
disp(K);(9)接下来根据新状态方程来生成闭环阶跃响应曲线图
% 构造闭环系统
sys_cl = ss(A - B * K, B, C, D);
figure;
step(sys_cl);
grid on;
title('连续状态空间下的LQR闭环阶跃响应');
xlabel('时间 (秒)');
ylabel('俯仰角 (度)');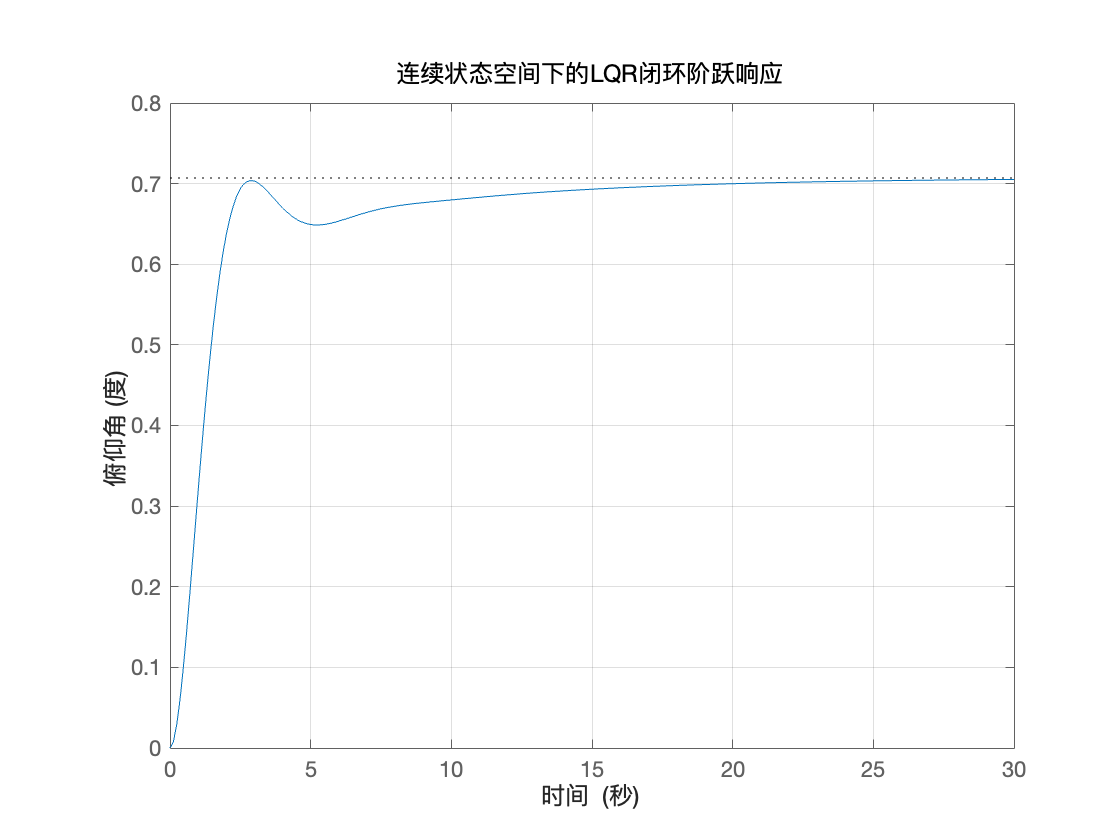
(10)明显可见,响应太慢,可以通过调整 LQR 来优化,具体的讲,就是增加加权因子 p 来完成,现在将 p=50
得到
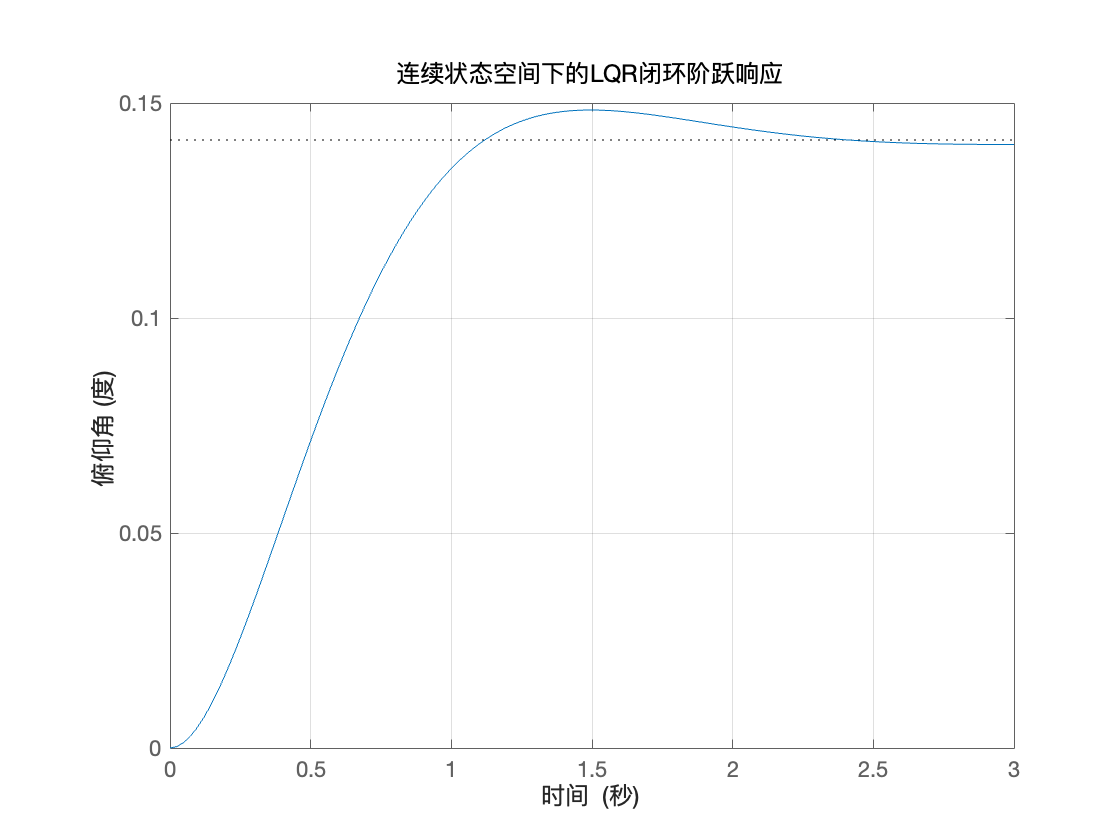
(11)比较不错,美中不足是和我们预设的阶跃信号 1 相差有点大,有没有办法让他最终稳定在 1 附近?此时 LQR 无能为力了,需要引入预补偿器 N(-)
添加预补偿器
注意,一直使用的全状态反馈系统并不是将输出值与参考输入值直接相比较,而是有个反馈矩阵K。因此为了获得所需要的输出可以缩放参考输入,使其输出在稳定时等于输入。加入预补偿器。
(12)因此得到了带有预补偿器的比例因子的状态反馈系统
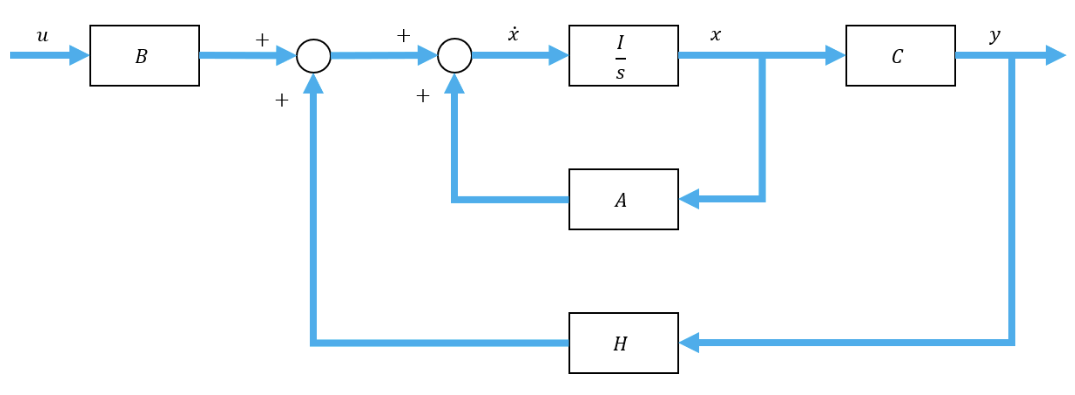
(13) 其中的比例因子 N (-)需要在用户定义函数(官方 help 文档中)`rscale.m` 中计算得到。该函数用于查找比例因子以消除稳态误差。
%% 连续状态空间法 - 添加预补偿器
% 计算预补偿器Nbar
Nbar = rscale(A, B, C, D, K); % 官方函数 rscale.m
disp(['预补偿器比例因子Nbar = ', num2str(Nbar)]);下面给出具体的函数代码
function Nbar = rscale(A, B, C, D, K)
% RSCALE calculates the scale factor Nbar to ensure zero steady-state error.
% Nbar adjusts the input to match the desired output.
%
% Usage:
% Nbar = rscale(A, B, C, D, K)
%
% Inputs:
% A, B, C, D - State-space matrices
% K - State feedback gain
%
% Output:
% Nbar - Input scaling factor
% Error check
if nargin < 5
error('Usage: Nbar = rscale(A, B, C, D, K)');
end
% Compute system size
n = size(A, 1);
% Form augmented system matrix
A_cl = A - B * K;
I = eye(size(A));
% Compute Nbar using the formula
Nbar = -inv(C * inv(A_cl) * B + D);
end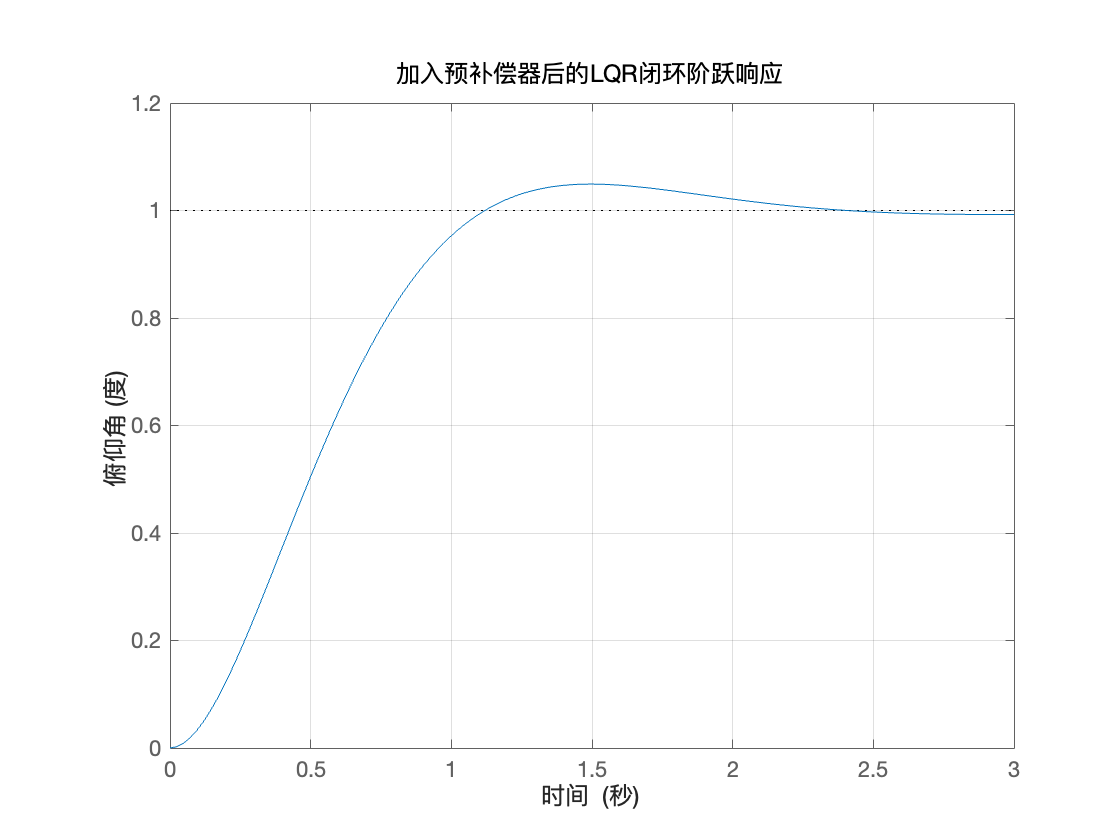
现在系统已经稳定在 1 附近,设计要求达到了。
(14) 注意:
添加的预补偿器 N (-)并不位于反馈回路中,这意味着如果存在未知干扰,预补偿器无法消除这部分偏差。换句话说,预补偿器的作用仅是对输入进行放大或缩小。例如,在此设计中,将输入放大了 7 倍,从而使输出从原来的 0.14 变为我们设定的 1(仅是振幅提高)。但从本质上说,稳态误差并未真正被消除。可以观察图中输出并未完全稳定在 1,原因在于 N 不在反馈回路内,因此无法真正改变输出的波形,也不能有效减少稳态误差。
一种改进的方法是将预补偿器与积分控制相结合。这样不仅可以缩放输出波形,同时还能在一定程度上减小稳态误差。
4.离散状态空间法-数字控制器设计法
(1)原连续时间状态方程如下,还是利用这个状态方程,但是现在想要得到新的离散时间状态空间方程
离散状态空间
(2) 要想设计数字控制系统,第一步必须使用 c2d 命令生成系统的采样数据模型(用编程从连续时间模型得到此模型)。而 c2d 命令需要三个参数:系统模型 + 采样时间 + 保持电路的类型。本实例中加入的是一个零阶保持电路(zoh)。
为了选择采样时间(防止漏信号),将采样频率与系统动态相比较,通常来讲,采样频率至少比闭环波特图的带宽频率大 30 倍。(带宽频率也称为闭环截止频率,是指当闭环幅频特性下降到频率为零时的分贝值以下 3 dB 时,对应的频率)
(额外补充:开环截止频率也称为剪切频率,是 开环幅频特性 中,幅频特性曲线穿越 0 dB 线的频率,记为 \omega_c ;闭环截止频率也称为带宽频率,是指当 闭环幅频特性曲线 下降到 -3 dB 时,对应的频率,记作 \omega_b 。开环 bode 图 ≠ 闭环 bode 图)
根据闭环波特图可得,带宽频率为 2 rad/sec,因此得到 0.01 s 的采样时间。
(3)使用c2d函数
%% 离散状态空间法 - 离散化与能控性检查
% 将连续系统离散化
Ts = 0.01; % 采样时间 (秒)
sys_d = c2d(ss(A, B, C, D), Ts, 'zoh');(4)因此就得到了离散时间状态空间模型
能控性
(5)与连续一样,必须验证离散系统可控性,依旧是算秩,方法同之前连续系统。
% 检查离散系统能控性
co_d = ctrb(sys_d.A, sys_d.B);
Controllability_d = rank(co_d);
disp(['离散系统能控性: Rank = ', num2str(Controllability_d)]);离散系统能控性: Rank = 3
极点布置进行控制设计
(6)和连续状态空间步骤一样,不过这次是离散全状态反馈控制系统
(7)同理得到矩阵
(8)同理使用 LQR 来找 K ,不过是 LQR 方法的离散版本
% LQR离散版本
p = 50; % 状态加权因子
Q_d = p * sys_d.C' * sys_d.C; % 离散状态成本加权矩阵
R_d = 1; % 控制权重矩阵
% 求解离散状态反馈增益矩阵K
[K_d] = dlqr(sys_d.A, sys_d.B, Q_d, R_d);
disp('离散LQR设计的反馈增益矩阵K:');
disp(K_d);(9) K 有了A-BK 就有了,离散状态方程所有量就都有了,直接看输出波形
% 构造离散闭环系统
sys_cl_d = ss(sys_d.A - sys_d.B * K_d, sys_d.B, sys_d.C, sys_d.D, Ts);
time = 0:Ts:10; % 仿真时间
theta_des = ones(size(time)); % 阶跃输入
[y, t] = lsim(sys_cl_d, theta_des, time);
% 绘制离散闭环系统的响应
figure;
stairs(t, y);
grid on;
title('离散LQR下的闭环阶跃响应');
xlabel('时间 (秒)');
ylabel('俯仰角 (度)');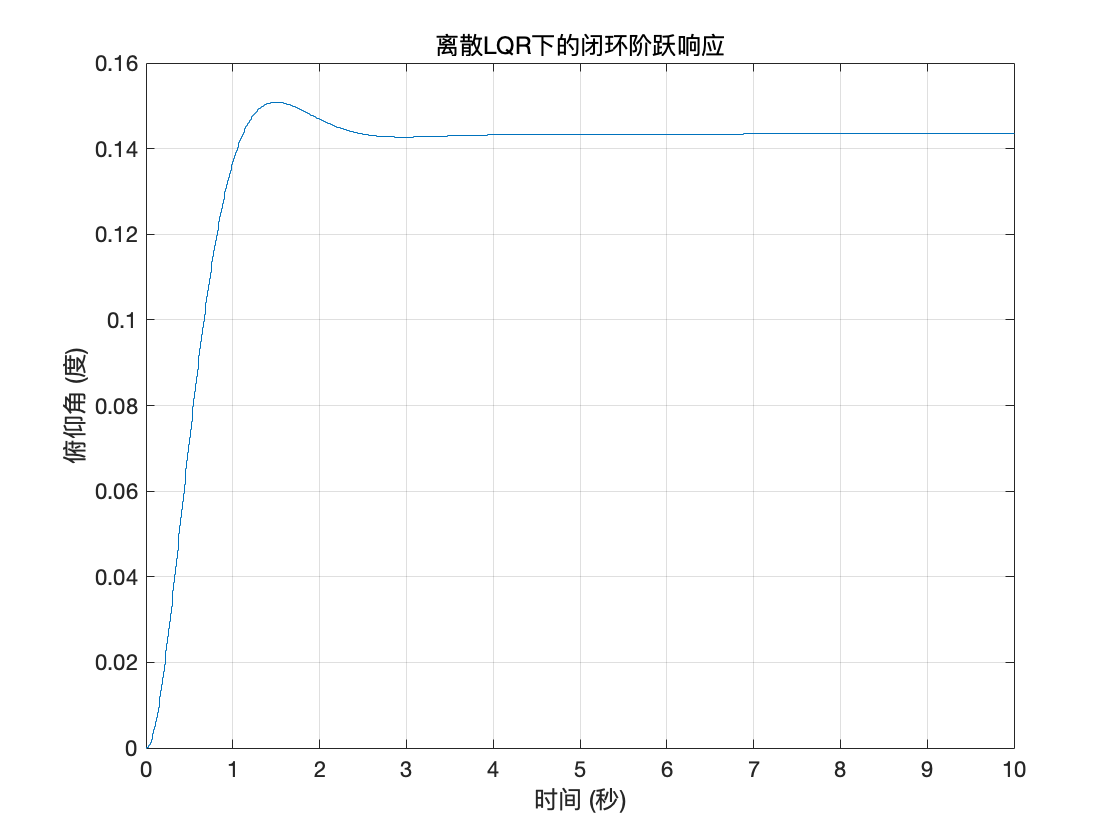
依旧还是离1差老远。
预补偿器
(10) 与连续不同的是,Nbar不能通过函数文件来自动算得了,因此只能手动调调改改。最后选定 N=6.95
%% 离散状态空间法 - 添加预补偿器
% 手动调整预补偿器比例因子
Nbar_d = 6.95; % 根据仿真调整的比例因子
disp(['离散系统预补偿器比例因子Nbar = ', num2str(Nbar_d)]);
% 构造加入预补偿器后的离散闭环系统
sys_cl_comp_d = ss(sys_d.A - sys_d.B * K_d, sys_d.B * Nbar_d, sys_d.C, sys_d.D, Ts);
[y_comp, t_comp] = lsim(sys_cl_comp_d, theta_des, time);
% 绘制加入预补偿器后的离散闭环响应
figure;
stairs(t_comp, y_comp);
grid on;
title('加入预补偿器后的离散LQR闭环阶跃响应');
xlabel('时间 (秒)');
ylabel('俯仰角 (度)');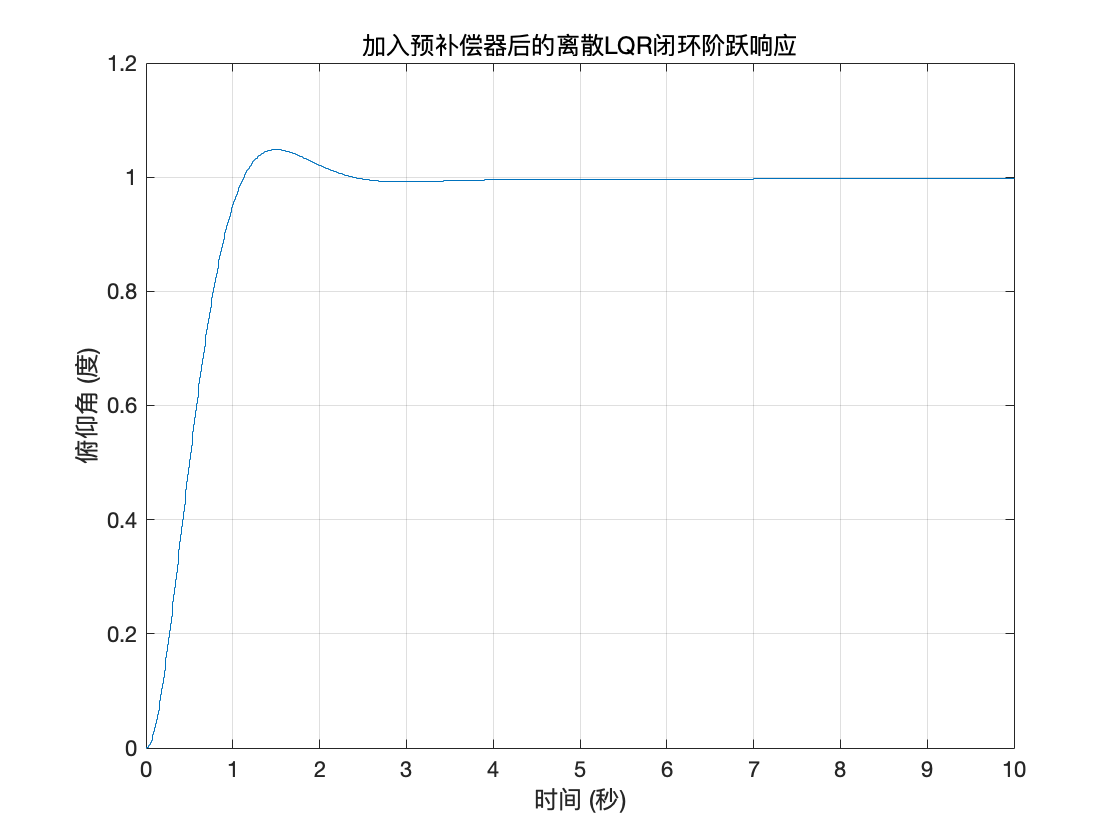
设计成功
5.PID法(不带脑子法)
PID的传函如下
我认为再多解释一个字都是对这个方法的不尊重
6.利用SIMULINK建立状况空间模型法
LQR
初步构建模型
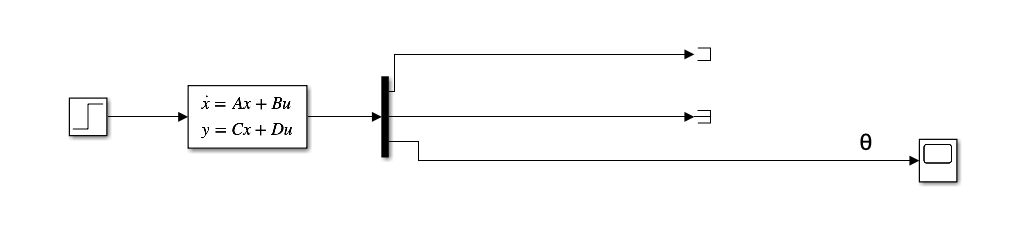
状态空间参数如下
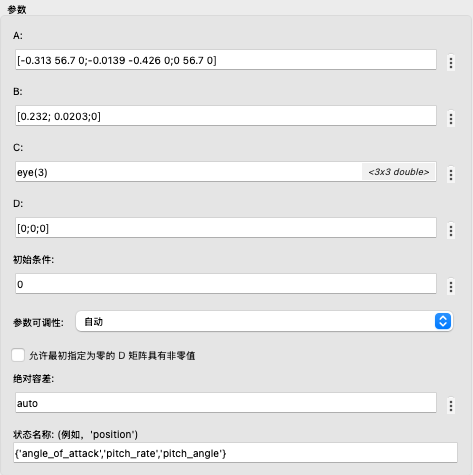
注:C 矩阵必须为 3 \times 3 的矩阵,而不是原方程中的 [0 \, 0 \, 1]。这意味着 C 矩阵的维度必须与矩阵 A 保持一致。可以使用 eye(3) 生成 3 \times 3 的单位矩阵。
在这种情况下,不仅将 \theta 视为输出,还将 \alpha 和 q 一起算作输出。因此,输出包含三条线,但实际上只有 \theta 的波形是需要重点关注的,其他两条可以忽略。
运行后,得到了开环阶跃响应(原始状态空间方程下)的输出波形
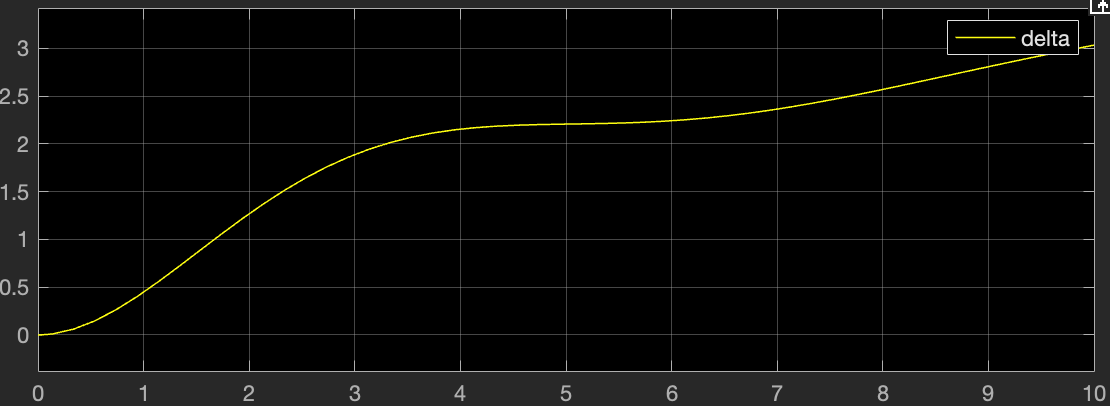
可见系统不稳定。参照以前的做法,我们将引入全状态反馈控制系统,这会将系统的状态矩阵变为 A - BK。接下来需要确定增益矩阵 K,这里利用 LQR 方法求解。为了提升稳态值,还引入了预补偿器。Simulink 模型中依旧按照这一流程进行。
通过代码计算,得到反馈增益矩阵:
将 K 加入系统后,全状态反馈控制系统就构成了。

预补偿器
接下来加入预补偿器。由于上面计算得出 N(-) = 7.0711 ,因此只需在系统中增加一个增益块,将输入乘以 N 即可实现预补偿。
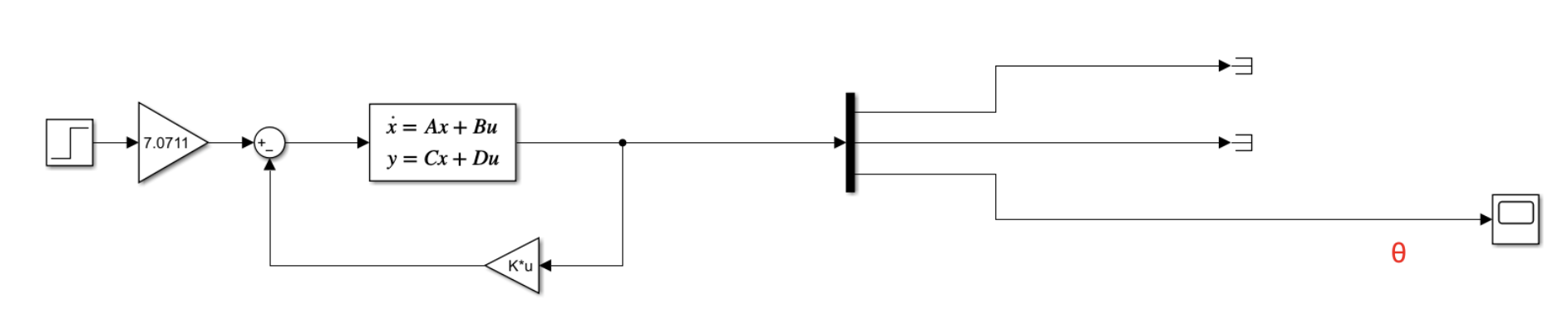
观察 \theta 输出波形已经稳定了,但是差点火候。特别是如果再添加一个扰动,那完蛋了,因为 LQR 的设计中并没有考虑到模型不确定性的鲁棒性,这也就是为什么 LQR 渐渐被 PID 淘汰,后面可以用 PID 来控制状态空间方程.
PID
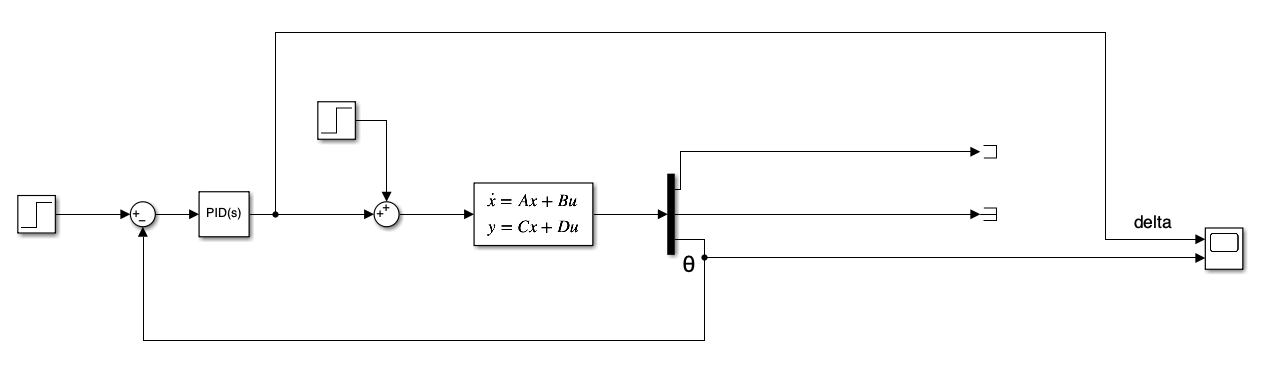
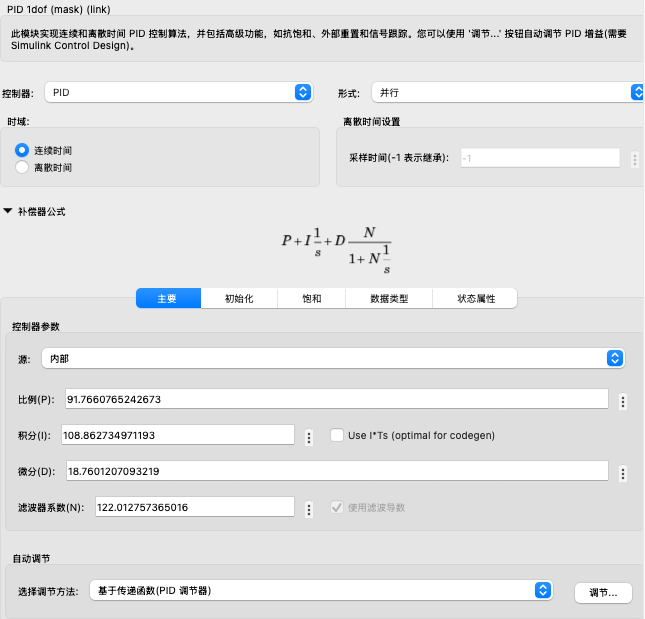
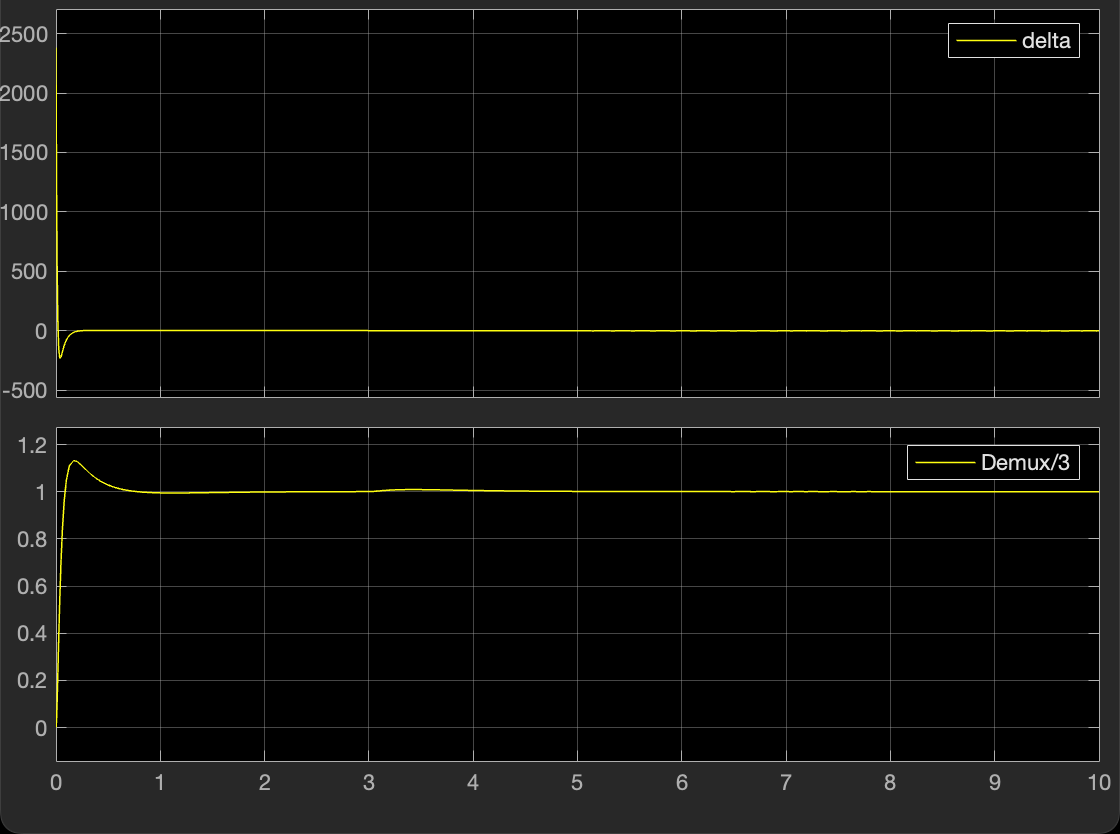
其中的滤波器系数 N 定义了微分项上一阶低通滤波器的时间常数,用于平滑微分信号,减少噪声对控制系统的影响。
可以在 PID 控制块的
Limit Output中设置控制器输出的饱和上下限。例如,对于飞机的升降角度,其范围很可能被限制在 -25° 到 +25°。加入饱和限制可以防止控制信号超出此范围,并用于自动调节 PID 参数以避免失控。但是,这样的设计也会引入积分饱和问题:当输出已经达到饱和限制时,积分器仍然继续工作,导致系统响应变得缓慢。为了解决这一问题,PID 控制块中提供了积分器抗饱和策略(在
PID Advanced选项中选择Anti-windup method)。这个模块会在积分饱和时立刻停止积分器的工作,而当输出恢复到非饱和状态时重新启用积分器。
版权说明
本内容框架和主题是基于 湖南工业大学控制实验室 所发布的教学内容的整理和进一步解释,仅供个人学习及复习回顾使用,我只是一个快乐的调包侠