定义

数据同化的作用就是在预测过程中不断利用新的观测数据来修正模型，使其误差不会随着时间推移而无限扩大。

以天气预报为例，短时间的天气预测通常比较准确，比如一小时后是否会下雨，这样基本手拿把掐。但如果要预测明天甚至后天的天气，准确度就不行了，这个时候观测数据就派上用场了，我们把观测数据融入数值天气预报模型中，每次融入就更新重制模型，比如说气象台每两小时得到的数据融入到NWP模型中，那么NWP每两小时就会被重制一次，重制之后的短时间内预测准确率较高，我们不断重复这个过程，这样预测值就在真实值周围不断波动，总体表现为: 重制-逐渐偏离-重制-逐渐偏离。

数据同化的“分析-预报”循环

分析（Analysis）：

就是之前说的 修正 模型过程，实际系统的观测量与模型产生的预报值相比较/融合，得到系统状态的最佳估计

预报（Forecasting）：

在这个阶段，基于修正过的模型，继续向前预测系统的未来状态，其预测仍然存在偏差，这个预测将持续到下一次新的观测数据到来，然后进入下一轮 分析 步骤，形成一个不断修正和优化的循环。

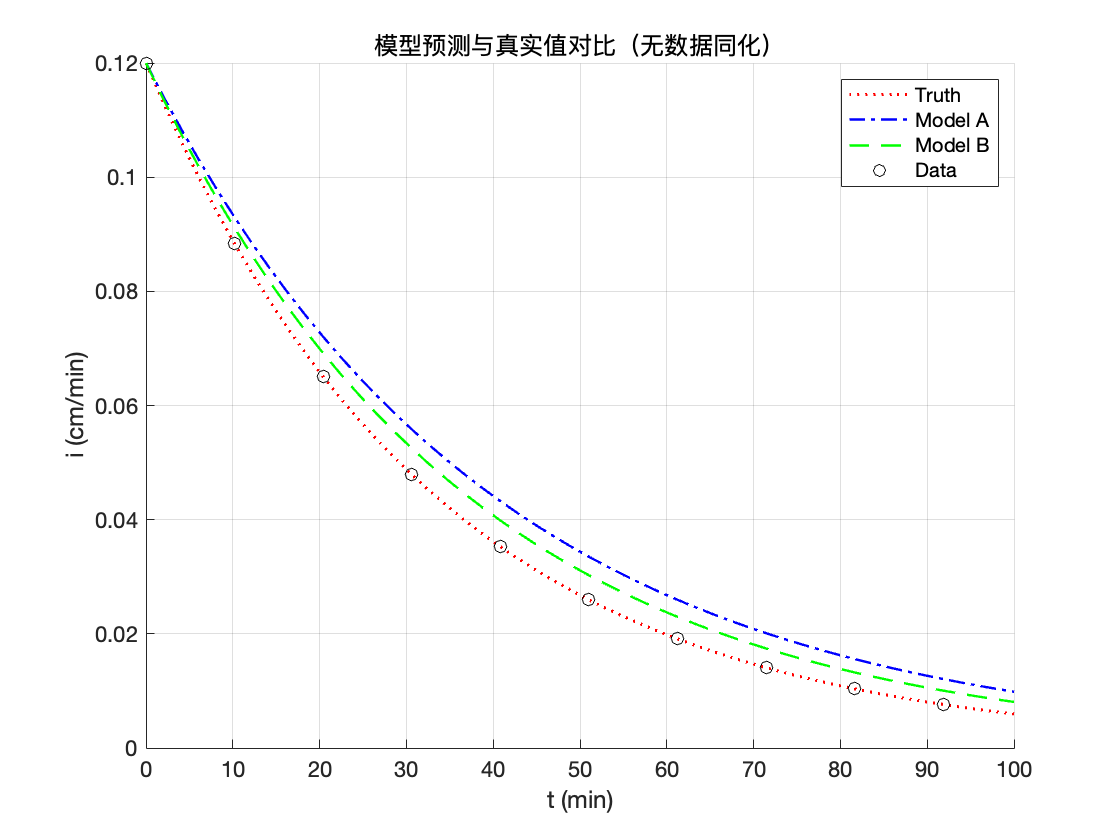
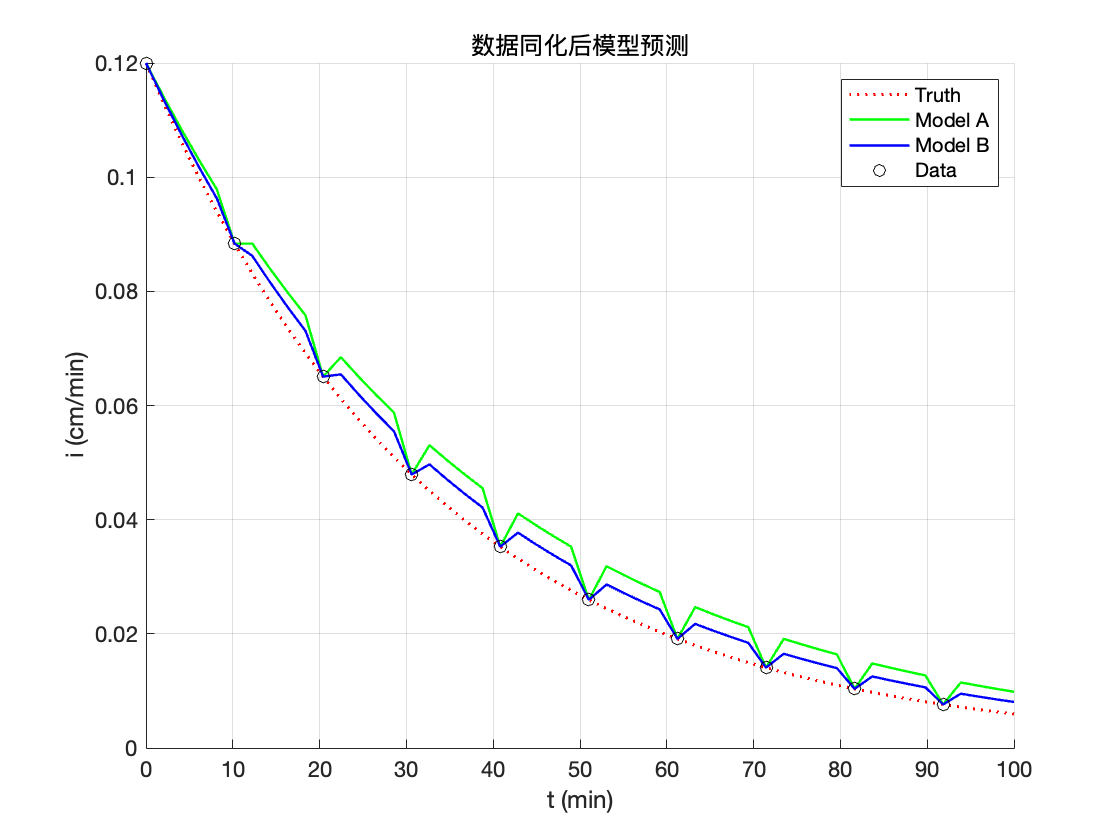
无偏差情况下数据同化模拟理解图

如果一言以蔽之，那就是模型模拟值和观测值根据方差进行加权平均。如果觉得观测值准确，那么其权重就大一些，反之同理。

数据同化与卡尔曼滤波

数据同化的数学原理可以与 卡尔曼滤波（Kalman Filter） 类比，卡尔曼滤波广泛用于动态系统状态估计的算法，它们的核心思想非常相似：

1. “分析”步骤 ≈ 观测值与预测值的校正

   • 在卡尔曼滤波中，系统的状态估计是基于 预测值 和 观测数据 之间的误差计算的。

   • 这里的“分析”步骤，就类似于计算 预测误差（观测值 - 预测值），并用这个误差来修正系统状态。

2. “预报”步骤 ≈ 计算系统状态的最优估计

   • 在卡尔曼滤波中，利用上一时刻的状态和系统动力学模型来预测下一时刻的状态。

   • 这个步骤相当于数据同化中的“预报”，即利用模型进行预测（但预测仍然存在偏差）。

数据同化与最优控制

与通常的最优控制（Optimal Control） 不同，数据同化的数据自由度极高，即状态变量的数量非常庞大，比如天气预报涉及全球范围内的大量气象数据，每个时间点都有数百万个变量需要处理，这种情况下无法求解协方差矩阵（最优控制是可以明确地计算整个系统的误差协方差的），因此需要近似方法来实现。