反问题:Wiener-Hunt 方法
编辑主要针对图像去模糊问题,即从模糊(带噪)图像中恢复清晰图像。这属于逆问题的范畴,一半出现在处理真实测量系统时。由于每个测量系统(如温度计、CCD相机、光谱仪等)都受到基础物理学的限制,比如有限精度、有限动态范围、非零响应时间等。这意味着测得的量或多或少都有扭曲。
大多数情况下,测量系统直接给出的测量数据通常具有足够的精度和鲁棒性。但是,也存在测量结果不准确的情况。为了解决精度问题,或者说至少部分地优化它,有特殊的信号和图像处理技术。在接下来的内容中,我们将通过一个简单的例子来展示此类方法。
我们有一张未聚焦的图像(即真实图像),这种情况下,点的图像实际上会是一个斑点。而捕获的图像是由真实图像中每个斑点的叠加结果,因此捕获的图像将会因为模糊而受损。我们现在尝试用一个数学模型来描述这种输入输出关系,最简单模型是线性不变滤波器,即卷积。
描述测量过程的方程(二维)如下:
x_{n,m} 代表真实或原始图像的像素(n, m),y_{n,m}代表观测到的图像的像素(n, m),或者更确切地说,是我们通过相机拍到的未聚焦图像。添加分量b_{n,m} 是为了考虑测量和建模误差。
P 和Q 是滤波器的尺寸,比如说一个3 \times 3 的滤波器,其P=1,Q=1,滤波器尺寸计算为(2P+1) \times (2Q+1)。
我们要做的事就是反转这个过程,从数学思维角度来讲,这个问题不难实现,但是我们有另外一个问题。
实际系统中的滤波器通常来说都是低通滤波器,高频分量在卷积过程中早就被丢弃了(要么被强烈衰减,要么完全被拒绝),我们无法在输出中再现输入信号或图像中的所有分量,这也就是“恢复真实信号”或者说“图像的逆问题”困难点:我们必须恢复那些要么被强烈衰减、要么完全不存在、要么“错误”观测到的高频分量。
我们下面使用的维纳滤波(Wiener Filtering)的变种 Wiener-Hunt 方法主要就是针对高频分量被强烈衰减的情况,它的前身是逆滤波(Inverse Filtering)方法,直接将传递函数或者说滤波器H(f) 构造成H^{-1}(f),也就是 \hat{X}(f) = \frac{Y(f)}{H(f)},但是这个方法有个极大的缺点,就是对噪声及其敏感,特别是在H(f) \to 0 的高频区域,会导致噪声爆炸。
再往后就使用 Wiener Filtering 算法,他通过最小化均方误差(MSE)实现,在已知滤波器H(f) 和噪声功率谱P_n(f) 及信号功率谱P_s(f) 的情况下,可计算维纳滤波器公式:
进此得到滤波后的信号:
这个方法思路非常漂亮,结合信号与噪声的统计特性,平衡了信号恢复与噪声抑制的效果,同时避免了在大噪声的情况下,噪声放大的问题,但是缺点也已经提到了,我们要先知道信号和噪声的统计特性 P_s(f) 和 P_n(f) ,如果没有统计信息的话就玩不了。此外,维纳滤波本质上处理的是全局最优问题,它对高频区域的恢复能力不是特别强。
因此 维纳滤波 的推广就是 Wiener-Hunt 方法,结合正则化思想和先验信息,将统计特性估计问题转化为一种迭代优化问题,即通过自适应求解来改进高频恢复效果和鲁棒性。在下面的例子中,我们用 Wiener-Hunt 线性方法来解决图像反卷积问题,他依赖于最小二乘准则,并结合了二次惩罚,其中的正则化项可以增强高频信号恢复和平滑噪声影响,并且正则化项还可以继续扩展DIY,满足不同问题情景
我们先介绍其理论部分,包括其损失函数及其最小化器。此外,提出了一种基于循环近似的方法,以实现矩阵求逆的快速数值计算。
1. 一维反卷积
为了简化理论概念,我们先讨论在一维情况下的信号反卷积。这种简化情况允许对反卷积问题的分析更加深入,同时更容易掌握概念和思路。随后再引入二维情况,并将其视为一维情况的扩展。Matlab 实现部分仅涉及二维情况。
1.1 一维建模
在一维情况下,(1) 中给出的观测模型变为:
如果我们有 N 个样本,可以将相应的 N 个方程写成矩阵形式:
向量 \mathbf{y} 包含了所有的 N 个观测值(在二维情况下,它将包含模糊的图像)
向量 \mathbf{x} 包含了恢复图像的样本 ,而 \mathbf{b} 是噪声样本。
矩阵\mathbf{H} ,称为模糊矩阵,是一个 N \times N 的方阵,具有以下经典结构:
更直观一点,一个具有 Toeplitz 结构的经典模糊矩阵 \mathbf{H} 表达式为:
例如,对于N = 5 和P = 3,模糊矩阵\mathbf{H} 的大小是5 \times 5,并且P = 3 表示核的支持范围是从-3 到3。矩阵的具体结构为:
因此,信号反卷积问题可以重新表述为:在已知观测信号\mathbf{y} 并知道卷积矩阵H 的情况下,估计向量\mathbf{x}。
1.2 带惩罚的最小二乘法
提出的重建策略(损失函数)是一种带惩罚的最小二乘法。它包含两个部分:
一个重构损失项或者叫数据拟合项,用于量化恢复信号\mathbf{x} 与观测信号\mathbf{y}进行重新卷积后的相似性,从而确保恢复的信号与观测信号一致。
一个惩罚项,用于限制恢复信号的连续样本之间的差异,确保其具有一定的规则性结构。
该 Penalty Least Squares 准则采用以下表达式:
其中, D是阶数为1,大小为(N - 1) \times N 的差分矩阵,定义如下:
一阶差分算子所描述的是图像像素之间的局部差异或梯度,一个好的图像通常在局部变化上是平滑连续的,出现突变 (边框)时,像素值的相邻差值将会较大。通过对相邻像素的差分约束,可以获得更平滑但仍能保留边缘信息的重建结果。
与此同时,一阶差分算子和二维差分滤波器在傅里叶域有对应的频率特征,可通过基本的线性运算(如FFT)高效计算,简单易实现。
带惩罚的最小二乘准则的最小化器为:
这就是我们反卷积得到的原始信号或图像。
证明
我们已知损失准则为:
继续展开:
求偏导为0:
特殊情况:
在特定情况下\mu = 0 时,准则和最小化器的结果表达式变为 J_{\text{PLS}}(x) = \|y - Hx\|^2
最小化器方程为:
此时准则变为经典的最小二乘问题,没有正则化项,也就是说,模型仅考虑最小化观测值与预测值之间的误差,而不会惩罚解的复杂度或平滑性。其解是经典的 最小二乘解。但是注意,这里并不是说去掉正则化项就变成 标准维纳滤波器 的形式了,因为 Wiener-Hunt 用的是最小二乘解(去掉正则化项后),而维纳滤波器用的是 最小化均方误差J_{MSE}(x) = \mathbb{E} \big[ \| \mathbf{x} - \mathbf{x}_{\text{true}} \|^2 \big],关注的是统计关系。
思考问题,如果不加这个\mu 会怎么样?即\mu =1 会怎么样?
1.2.1 循环近似
回到反卷积后的原始信号的恢复公式:
可见 Wiener-Hunt 方法的理论其实并不难,但是实际实践起来却有一个问题,那就是矩阵H^T H + \mu D^T D 的大小为N \times N,当N 很大时,这种反演根本算不了,比如说在处理图像时,对于1000 \times 1000 的图像,矩阵的大小为10^6 \times 10^6,没个玩儿。在三维情况下,更复杂。我们现在必须想办法克服这个逆计算的困难。
为了计算\hat{x},有几种方法可以解决这个问题。
我们这里选用的方法是使用循环矩阵的特性,用对角矩阵来 “替换” 上面公式中的矩阵(通过快速傅里叶变换 FFT 可以将循环矩阵 “转化”为对角矩阵)。因此,使用对角矩阵进行计算时,乘法或反演等矩阵运算的复杂度将大大降低。思路非常好,所以现在需要先将矩阵H 和D 近似为循环矩阵\tilde{H} 和\tilde{D}。
循环近似涉及修改矩阵的右上角和/或左下角部分,使其具有循环结构。
这种近似有两个前提条件:
信号或图像是周期循环不结束的,换句话说,信号是首尾相连的环状结构
矩阵具有 Toeplitz 结构,所有对角线元素相同。
例如给定 Toeplitz 矩阵:
将矩阵的“非循环”部分补齐,使其具有循环特性。我们需要将矩阵的右上角和左下角部分填充为一个“循环”模式。在具体的这个实例中,我们使用模5重索引方法,基于序列的循环性(周期性)假设序列\{h_k\} 在索引上是按照长度为5的周期重复的,因此:
h_{-1}取模5后:-1 \mod 5 = 4,因此h_{-1} = h_4
h_{-2}取模5后:-2 \mod 5 = 3,因此h_{-2} = h_3
h_{-3}取模5后:-3 \mod 5 = 2,因此h_{-3} = h_2
H 的循环矩阵为:
D 的近似循环矩阵为:
得到的循环卷积矩阵\tilde{H} 和\tilde{D} 在傅里叶基下可以轻松对角化:
矩阵\Lambda_h 是对角矩阵,其对角线上元素是H 的特征值。
计算\Lambda_h 或\Lambda_d 特征值的方法,就是对矩阵H 或D 第一行进行快速傅里叶变换(FFT)获得,FFT(H的第一行) = 结果矩阵,\Lambda = \text{diag}(结果矩阵),其实其本质是计算脉冲响应的N 点 FFT。同样适用于矩阵\tilde{D} 及其特征值,其中将脉冲响应替换为[-1, 1]。
由于使用FFT来计算得到特征值并组成对角矩阵来简化计算矩阵的逆,我们因此可以将计算复杂度降低至N\log N,即FFT 复杂度。
将上式对角化方法带入原公式中可以得到:
在此基础上再进一步:
FT_x = 1 ./ (abs(Lambda_H).^2 + mu * (abs(Lambda_dC).^2 + abs(Lambda_dR).^2)).* (conj(Lambda_H).* FT_Data);在 Matlab 中以如下方式实现,其中 MyFFT2RI 是自定义函数,在实现部分给出。
\Lambda_h \Rightarrow FT_IR = MyFFT2RI(IR, 256);
\Lambda_{d_c} \Rightarrow FT_Dc = MyFFT2RI(Dc, 256);
\Lambda_{d_r} \Rightarrow FT_Dr = MyFFT2RI(Dr, 256);
补充知识:\tilde{H} 是一个实矩阵,因此其复共轭等于它本身(无虚部), H = \overline{H}。 \tilde{D} 同理。
在近似为循环矩阵后,公式 变为:
其中:\tilde{H} = F^\dagger \Lambda_h F 且\tilde{D} = F^\dagger \Lambda_d F 将其带入上述公式,得:
因为傅里叶矩阵F 是一个正交矩阵,具有F F^{\dagger} = I 的性质,即F^{\dagger} = F^{-1}。这里请注意,F 是复值DFT矩阵,是酉矩阵,F^\dagger 表示共轭转置,并非简单的转置。并且我们有(F^{\dagger}\Lambda_{h}F)^{T} = F^{\dagger}\Lambda_{h}^{T}F 以及(F^{\dagger}\Lambda_{d}F)^{T} = F^{\dagger}\Lambda_{d}^{T}F
所以:
令\overset{\circ}{\hat{x}} = F \hat{x},\overset{\circ}{y} = F y
那么:
特殊情况:
当 \mu = 0 时,正则化项消失,公式简化为:
这意味着我们仅仅得到了没有考虑图像的正则化的 经典最小二乘方法 的解,虽然理论上可以恢复原始信号,但是实际上收到的噪声影响很大,且没有约束来将其消除。
我们回到之前利用近似循环矩阵后得到的恢复信号方程:
对角矩阵有如下性质:
也就是对角矩阵可以无视一切共轭转置
因此有:
逐元素表达形式:
这个形式看着太丑了,为了给他打扮一下,我们将其改造成 g_{PLS}^{n} 形式
g_{PLS}^{n} 代表的是向量g_{PLS} 中的每个分量。
因此,向量\overset{\circ}{\hat{x}} 是通过向量g_{\text{PLS}} 和\overset{\circ}{\hat{y}} 之间逐元素相点积得到的:
反卷积问题可以表述为在傅里叶域中进行的滤波操作,其中 g_{\text{PLS}} 代表离散传递函数。
综上所述,我们重新列出所有理论公式:
① 观测模型(一维):
② 该 Penalty Least Squares 准则损失函数:
③ 带惩罚的最小二乘准则的最小化器为:
④ 近似为循环矩阵并利用傅立叶基得到对角矩阵,上述公式重写为
⑤ 对角矩阵可以无视一切共轭转置,上述公式重写为
⑥ 其分量n = 1, 2, \dots, N 计算形式为
⑦ 最终得到原始图像的恢复公式,为频域中的向量点积形式:
⑧ 我们再进行反快速傅立叶变换即可得到空间域想要的原始输入信号或图像:
算法流程总结如下:
① 构建\mathring{h} 作为脉冲响应的N 点 FFT
② 构建\mathring{d} 作为[1; -1] 的N 点 FFT
③ 构建包含传递函数g_{\text{PLS}} 的向量
④ 构建观测值的 FFT\mathring{y}
⑤ 计算\mathring{\hat{x}},作为传递函数g_{\text{PLS}} 和\mathring{\hat{y}} 的乘积
⑥ 计算\mathring{\hat{x}} 的 IFFT 以在空间域中获得解\hat{x}
2 实现
2.1 二维方法
对于二维情况,其方程类似于一维情况。但是,所涉及的block-Tœplitz矩阵结构更加复杂: 每个块本身也具有 Tœplitz 结构。这使得在两个方向上进行循环近似变得更加困难。因此,二维情况仅作为一维情况的扩展来展示,重点是 Matlab 实现,理论部分暂不讨论。
注意以下几点:
图像、脉冲响应、正则化项都是二维的,这意味着必须使用 FFT-2D 而不是 FFT。
更确切地说,如果要恢复的图像有 N 行和 N 列,那么 FFT-2D 必须在 N 行和 N 列上计算。
频率传递函数也是二维的,每个空间频率有一个维度。
特别说明 — 在任何情况下,矩阵 H 和 D 都不应在 Matlab 代码中构建。
2.2 观测图像
第一步是加载数据 Data1 和 Data2 。使用 load 函数来完成。每个数据文件内部包含:模糊图像 (Data)、用于比较的真实图像 (TrueIma),以及卷积滤波器的脉冲响应 (IR)。现在分析每个数据集及其相互关系。
clear all
close all
clc
%% Load Data
Data1 = load('DataOne.mat')
Data2 = load('DataTwo.mat')
% Create a window to display the image
figure()
subplot(1,2,1)
% Display the image, grayscale
imagesc(Data1.Data);
colormap('gray');
% Scale the axes and eliminate the grading
axis('square','off')
title('Observed Image - Data1');
subplot(1,2,2)
% Display the image, grayscale
imagesc(Data2.Data);
colormap('gray');
% Scale the axes and eliminate the grading
axis('square','off')
title('Observed Image - Data2');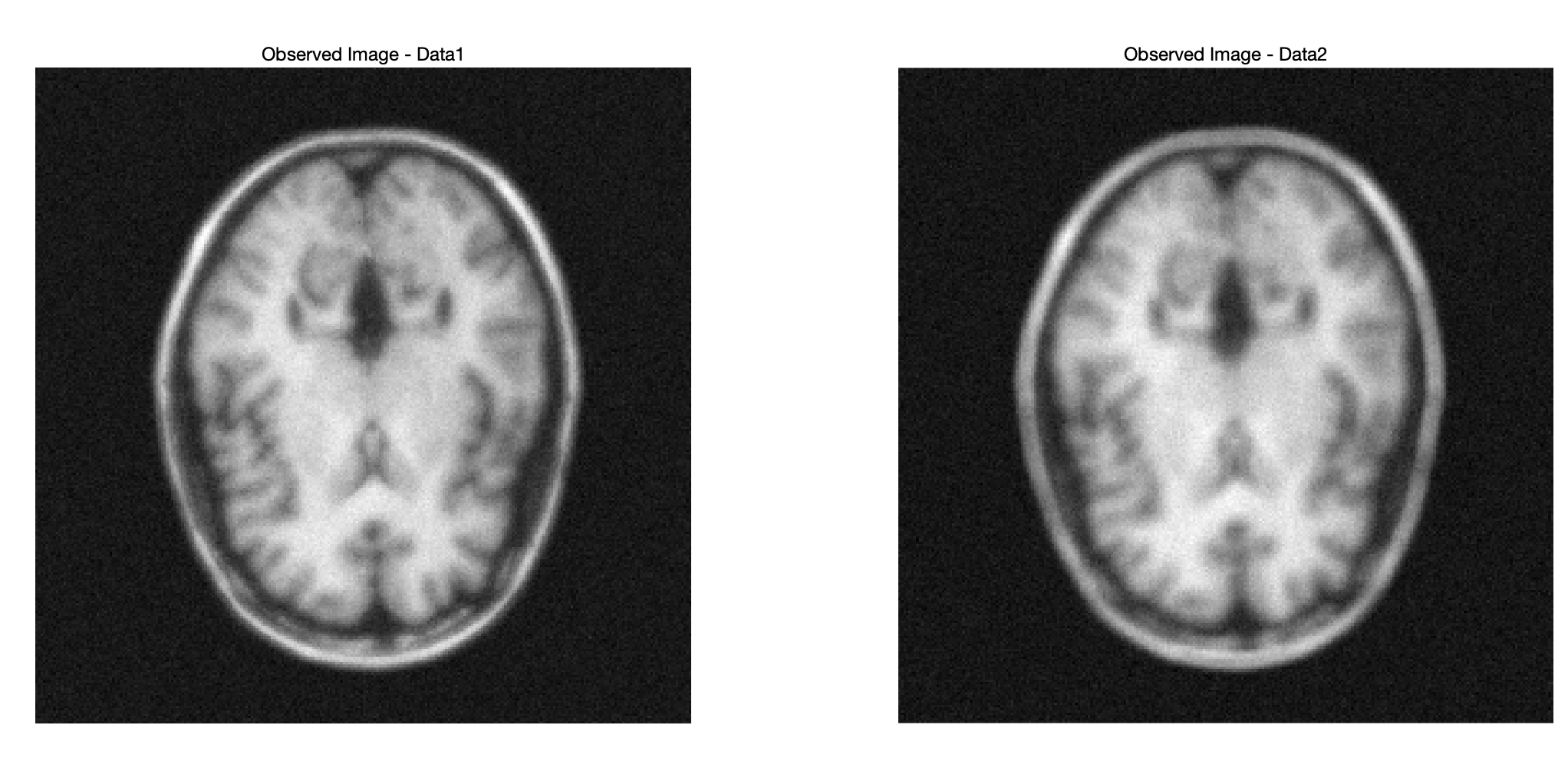
两观测图像都有明显的模糊,具体是边缘和结构细节处。这种模糊表明图像中的高频信息被卷积或散射了,导致图像细节的丢失,这就是由于卷积效应或低通滤波的影响而造成的。
为了进一步分析,肯定要到频域看
%% Analyse the images in the frequency domain (linear and a logarithmic scale)
% % Get the sizes of the images
% [M1,N1] = size(Data1.Data);
% [M2,N2] = size(Data2.Data);
% % Generate frequency axes for Data1
% u1 = (-M1/2:M1/2-1)/M1; % Normalized frequencies in y-direction
% v1 = (-N1/2:N1/2-1)/N1; % Normalized frequencies in x-direction
% % Generate frequency axes for Data2
% u2 = (-M2/2:M2/2-1)/M2;
% v2 = (-N2/2:N2/2-1)/N2;
% Generate normalized frequency axes using linspace
Nu = linspace(-0.5, 0.5, 256);
% Compute the 2D FFT of observed images and shift zero frequency to center
FFT_Data1 = MyFFT2(Data1.Data);
FFT_Data2 = MyFFT2(Data2.Data);
% Magnitude spectra
Mag_Data1 = abs(FFT_Data1)
Mag_Data2 = abs(FFT_Data2)%% MyFFT2
function Frequentiel = MyFFT2(Spatial)
% MyFFT2
% 对二维空间域数据 Spatial 进行 2D FFT,并对结果进行 fftshift 和归一化处理。
%
% 输入参数:
% Spatial : 二维时域(或空间域)数据矩阵
%
% 输出参数:
% Frequentiel : 已经经过 fftshift 和归一化的二维频域数据矩阵
Frequentiel = fftshift( fft2(Spatial) ) / length(Spatial);
end
%% MyFFT2RI
function Frequentiel = MyFFT2RI(Spatial, Long)
% MyFFT2RI
% 对输入的二维数据 Spatial 进行补零扩展至尺寸 Long x Long,以便在频域处理时
% 保持良好的居中对齐。补零后对数据进行 fftshift、2D FFT 再 fftshift。
%
% 输入参数:
% Spatial : 原始二维数据矩阵
% Long : 补零后的目标矩阵尺寸(长宽相等)
%
% 输出参数:
% Frequentiel : 已补零扩展并居中对齐的二维频域数据矩阵
Taille = length(Spatial);
Ou = 1 + Long/2 - (Taille-1)/2 : 1 + Long/2 + (Taille-1)/2;
SpatialComplet = zeros(Long, Long);
SpatialComplet(Ou, Ou) = Spatial;
Frequentiel = fftshift( fft2( fftshift(SpatialComplet) ) );
end
%% MyIFFT2
function Spatial = MyIFFT2(Frequentiel)
% MyIFFT2
% 对二维频域数据执行逆FFT操作并进行 fftshift 和归一化,以还原回空间/时域信号。
%
% 输入参数:
% Frequentiel : 二维频域数据矩阵(已 fftshift)
%
% 输出参数:
% Spatial : 逆变换并归一化后的二维时域(空间域)数据矩阵
Spatial = ifft2( fftshift(Frequentiel) ) * length(Frequentiel);
end% Display magnitude spectra in linear scales
figure();
subplot(1,2,1)
imagesc(Nu,Nu,Mag_Data1); % Use frequency axes v1 and u1
xlabel('X');
ylabel('Y');
colormap('gray');
title('Magnitude (Linear Scale) - Data1');
subplot(1,2,2)
imagesc(Nu,Nu,Mag_Data2); % Use frequency axes v2 and u2
xlabel('X');
ylabel('Y');
colormap('gray');
title('Magnitude (Linear Scale) - Data2');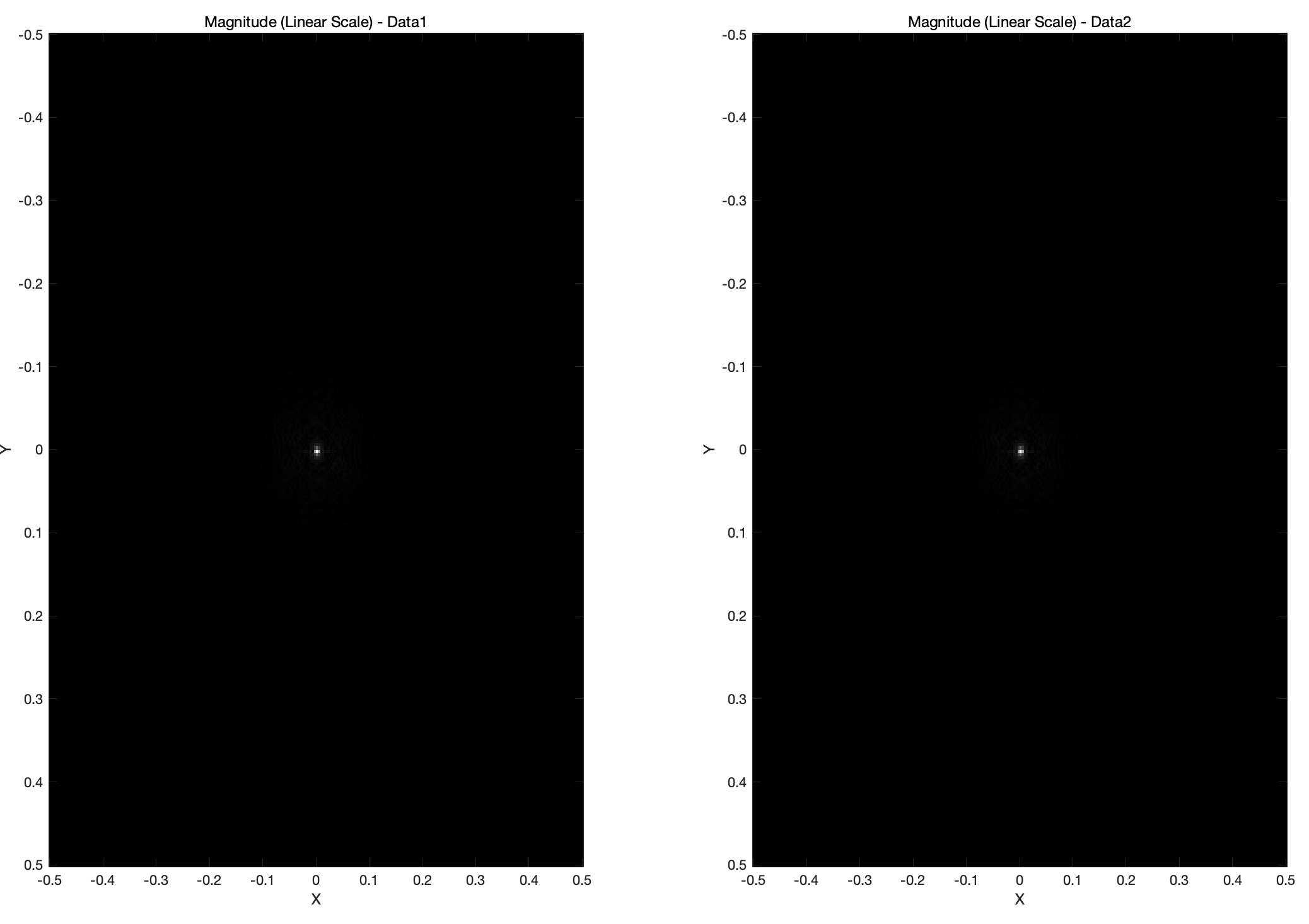
% Display magnitude spectra in logarithmic scales
figure;
subplot(1,2,1)
imagesc(Nu,Nu,log(1+Mag_Data1)); % Use log scale
xlabel('X');
ylabel('Y');
colormap('gray');
title('Magnitude (logarithmic Scale) - Data1');
subplot(1,2,2)
imagesc(Nu,Nu,log(1+Mag_Data2));
xlabel('X');
ylabel('Y');
colormap('gray');
title('Magnitude (logarithmic Scale) - Data2');
可见只有两组频谱图的中心部分有强烈亮度,即低频分量较强,即图像大范围平滑信息较多,而高频部分的细节没有
我们继续看两个脉冲响应h_{n,m} 及其关联的传递函数H(\nu_x, \nu_y)。首先使用
imagesc函数,然后使用plot函数来进行分析。
%% Calcul impulse responses and associated transfer functions using impulse
% Load the impulse responses
IR1 = Data1.IR;
IR2 = Data2.IR;
% Display the impulse responses
figure;
subplot(1,2,1)
imagesc(IR1);
colormap('gray');
title('Impulse Response - IR1');
subplot(1,2,2)
imagesc(IR2);
colormap('gray');
title('Impulse Response - IR2');
% Compute and display the transfer functions
Long = 256;
H1 = MyFFT2RI(IR1, Long);
H2 = MyFFT2RI(IR2, Long);
% Compute the magnitude spectra
Mag_H1 = abs(H1);
Mag_H2 = abs(H2);
% Display the transfer functions using imagesc
figure;
subplot(1,2,1)
imagesc(Nu, Nu, Mag_H1);
xlabel('X');
ylabel('Y');
title('Transfer Function Magnitude - H1');
colormap('gray');
subplot(1,2,2)
imagesc(Nu, Nu, Mag_H2);
xlabel('X');
ylabel('Y');
title('Transfer Function Magnitude - H2');
colormap('gray');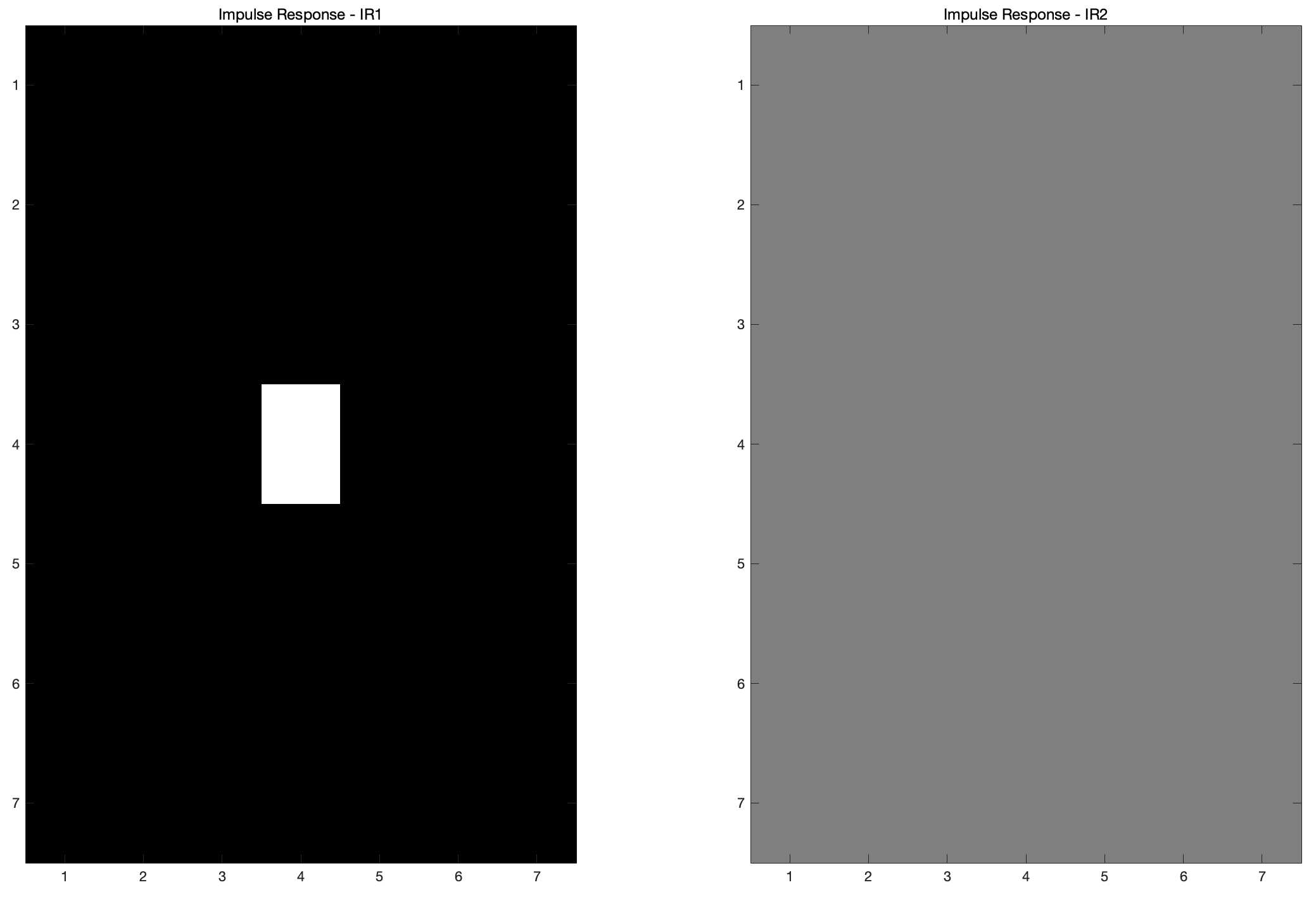
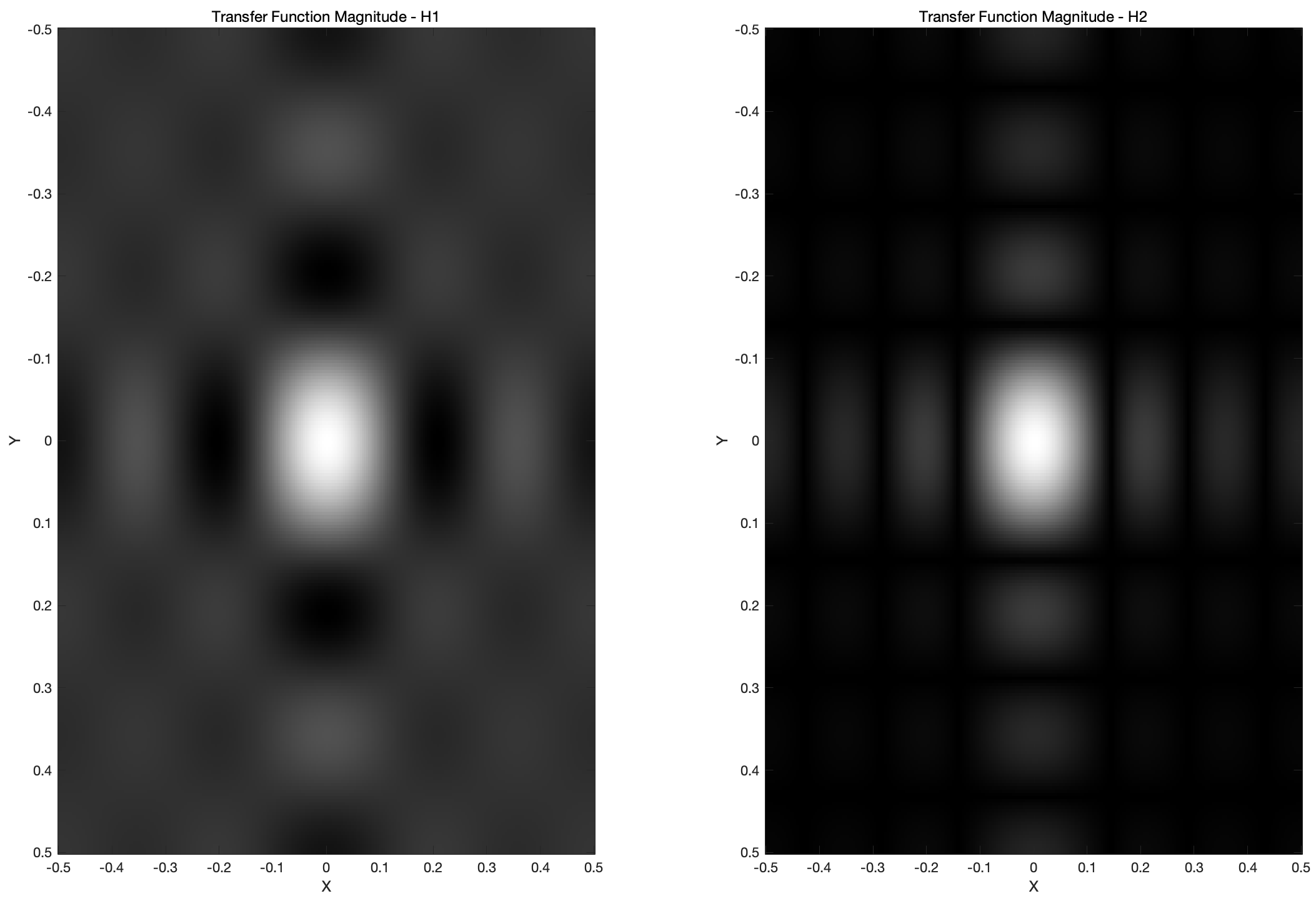
很明显,IR1 和 IR2 都是低通滤波器,只允许低频分量通过,高频分量进行衰减或完全抑制。IR1 的传递函数 H1 的分布更加平滑,说明它对低频分量的保留更为均匀。IR2 的滤波特性更倾向于选择性地保留某些低频分量,而非均匀地平滑整个低频区域。因此,相较于 IR1,IR2 对图像的细节影响更强。不过这么看看不出来具体的道道儿,还是得看下面的切片。
%% Plot slices through the transfer functions using plot
% Midpoint index (since Long = 256)
mid_index = Long / 2 + 1; % This will be 129
% Plot slices for H1
figure;
subplot(2,1,1)
plot(Nu, Mag_H1(mid_index, :));
xlabel('Normalized Frequency X');
ylabel('Magnitude');
title('Transfer Function along Central Row - H1');
grid on;
subplot(2,1,2)
plot(Nu, Mag_H1(:, mid_index));
xlabel('Normalized Frequency Y');
ylabel('Magnitude');
title('Transfer Function along Central Column - H1');
grid on;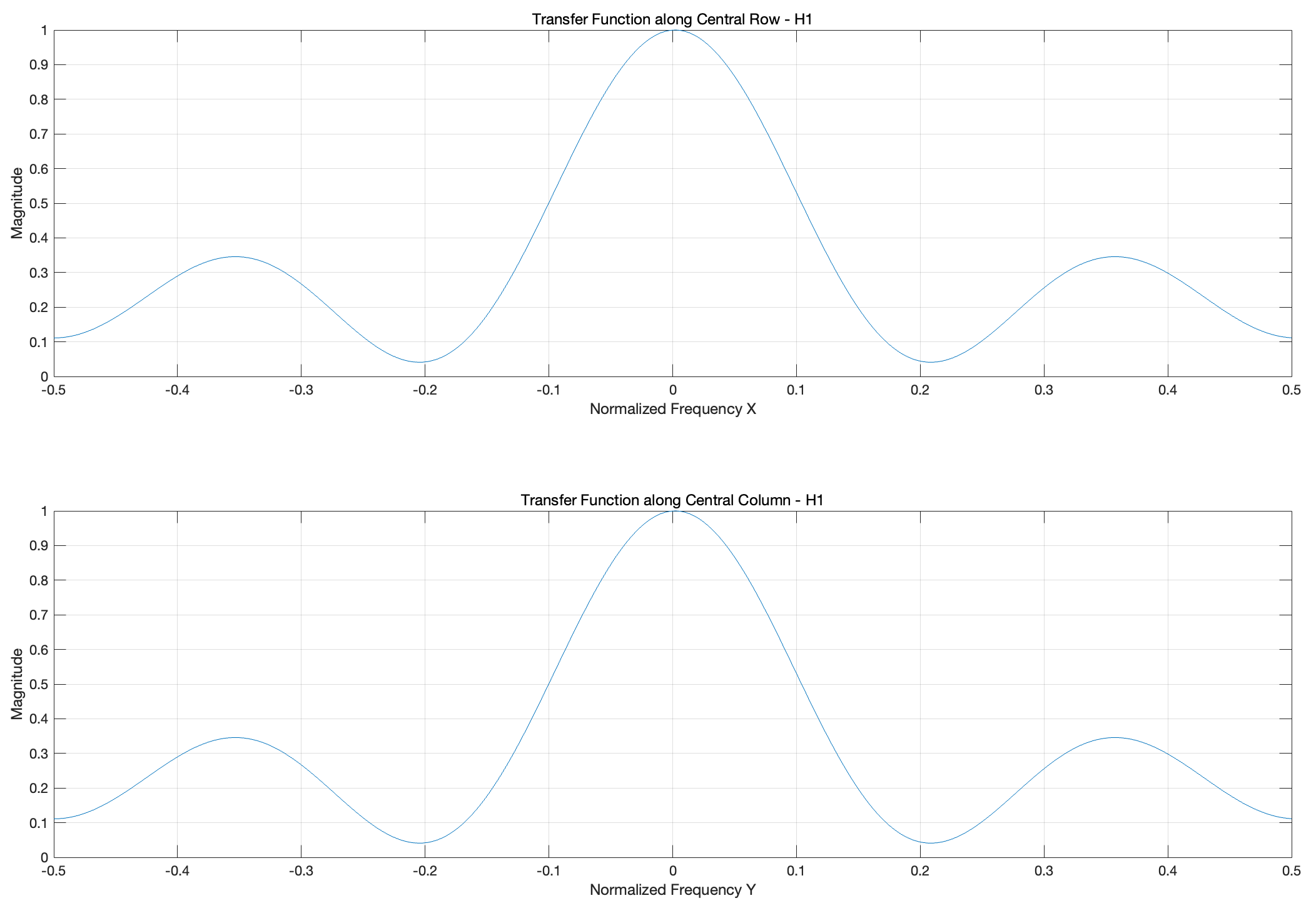
可见前面的结论是正确的,H1 幅值响应曲线变化相对平滑,适合图像整体的模糊处理任务。
% Plot slices for H2
figure;
subplot(2,1,1)
plot(Nu, Mag_H2(mid_index, :));
xlabel('Normalized Frequency X');
ylabel('Magnitude');
title('Transfer Function along Central Row - H2');
grid on;
subplot(2,1,2)
plot(Nu, Mag_H2(:, mid_index));
xlabel('Normalized Frequency Y');
ylabel('Magnitude');
title('Transfer Function along Central Column - H2');
grid on;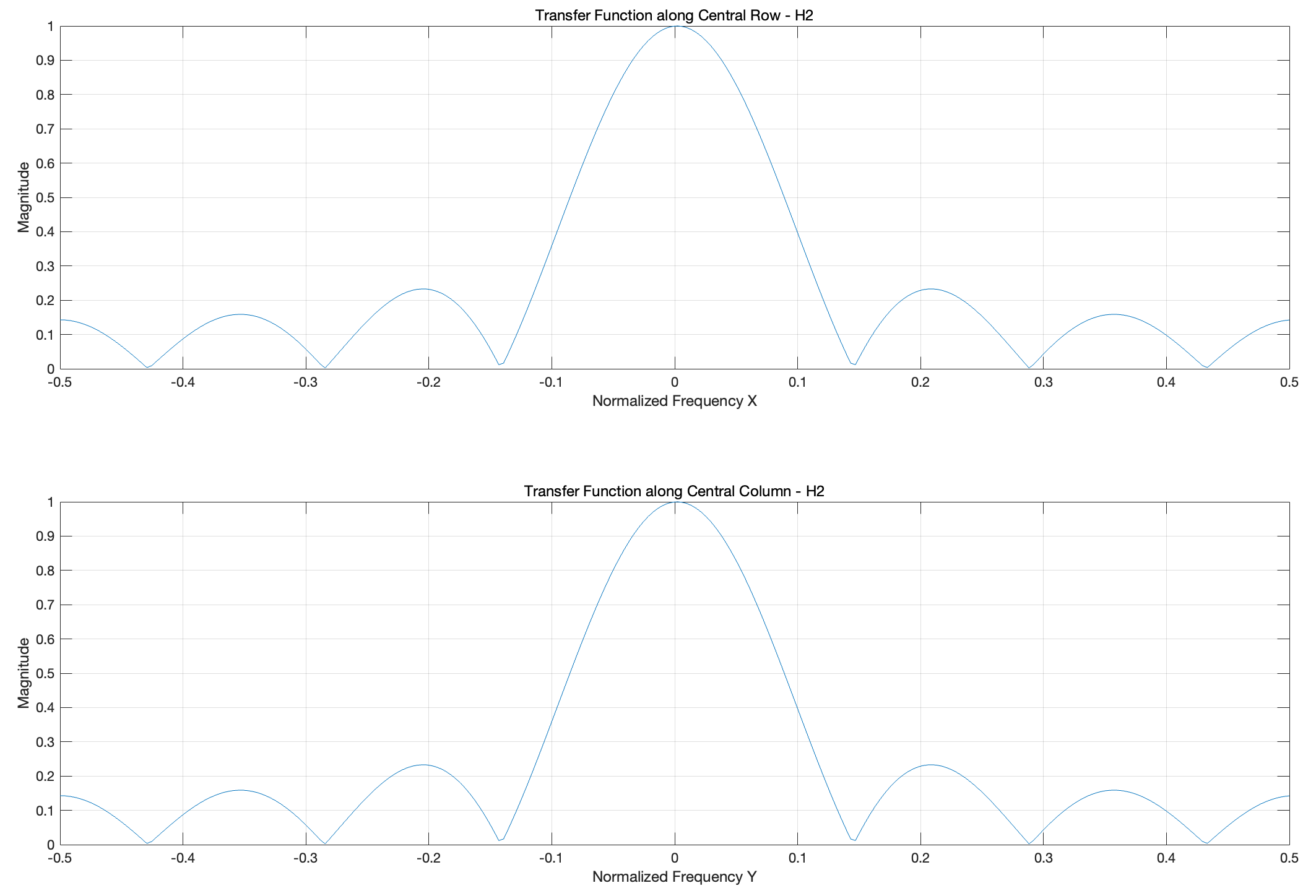
在 H2 的切片图中,幅值响应曲线有更明显的周期性波动,适合特定方向的模糊或增强效果。
2.3 Implementation
我们将在二维情况下实现反卷积,并使用带有二次惩罚项的最小二乘法,同时使用循环近似进行最小化,在前面已经进行过了总结。
关于正则化项,它依赖于图像列和行上相邻像素之间的差异。其表达式为:
正则化项| D x |^2 代表了水平方向和垂直方向相邻像素值的平方差之和。
因此它将基于两个滤波器(水平和垂直)来实现:
这两个滤波器分别计算行和列上像素之间的差异。
当然也可以从以下脉冲响应滤波器中选一个,它们都可以实现图像梯度的近似。
回顾前面,我们得到:
现在进行傅里叶变换下的去卷积
\hat{H}(\nu_{x}, \nu_{y}) 是卷积矩阵的傅里叶变换
\hat{D}(\nu_{x}, \nu_{y}) 是差分矩阵的傅里叶变换
\hat{x}(\nu_{x}, \nu_{y}) 是频域中的恢复图像
我们先写一个反卷积函数,将观测数据 (Data)、脉冲响应 (IR) 和正则化参数 (mu) 作为输入。
function [x] = deconvolve_image(Data,IR,mu)
Long = length(Data);
Nu = linspace(-0.5, 0.5, Long);
TF_Data = MyFFT2(Data);
TF_IR = MyFFT2RI(IR,Long);
% figure(1)
% subplot(2, 1, 1)
% imagesc(Nu, Nu, abs(TF_IR))
% title('Frequency response')
% xlabel('\nu_x')
% ylabel('\nu_y')
% axis square
% subplot(2, 1, 2)
% plot(Nu, abs(TF_IR(round(length(TF_IR)/2), :)))
% Define the regularization filters (difference operators)
% Horizontal difference filter
Dh = [0 0 0; 0 -1 1; 0 0 0];
% Vertical difference filter
Dv = [0 0 0; 0 -1 0; 0 1 0];
% Compute the FFTs of the regularization filters using MyFFT2RI
TF_Dh = MyFFT2RI(Dh, Long);
TF_Dv = MyFFT2RI(Dv, Long);
% Compute |Dh|^2 and |Dv|^2
abs_Dh_squared = abs(TF_Dh).^2;
abs_Dv_squared = abs(TF_Dv).^2;
% Total regularization term |D|^2 = |Dh|^2 + |Dv|^2
abs_D_squared = abs_Dh_squared + abs_Dv_squared;
% Compute the denominator of the Wiener filter
denom = abs(TF_IR).^2 + mu * abs_D_squared;
% Compute the numerator
numerator = conj(TF_IR) .* TF_Data;
% Compute X_hat in the frequency domain
TF_X = numerator ./ denom;
% Compute the inverse FFT to get the deconvolved image
% Since MyFFT2 uses fftshift, we need to use ifftshift before ifft2
x = MyIFFT2(TF_X);
end然后应用这个逆卷积函数,查看反卷积后的图像去噪效果。
%% Question 5
mu = 0.004;
% Deconvolve Data1
x_1 = deconvolve_image(Data1.Data, Data1.IR, mu);
% Display the deconvolved image
figure;
subplot(1,2,1)
% Display the image, grayscale
imagesc(Data1.Data);
colormap('gray');
% Scale the axes and eliminate the grading
axis('square','off')
title(['Observed Image - Data1, \mu = ', num2str(mu)]);
subplot(1,2,2)
imagesc(x_1);
colormap('gray');
title(['Deconvolved Image - Data1, \mu = ', num2str(mu)]);
axis('square','off')
% Deconvolve Data2
x_2 = deconvolve_image(Data2.Data, Data2.IR, mu);
% Display the deconvolved image
figure;
subplot(1,2,1)
% Display the image, grayscale
imagesc(Data2.Data);
colormap('gray');
% Scale the axes and eliminate the grading
axis('square','off')
title(['Observed Image - Data2, \mu = ', num2str(mu)]);
subplot(1,2,2)
imagesc(x_2);
colormap('gray');
title(['Observed Image - Data2, \mu = ', num2str(mu)]);
axis('square','off')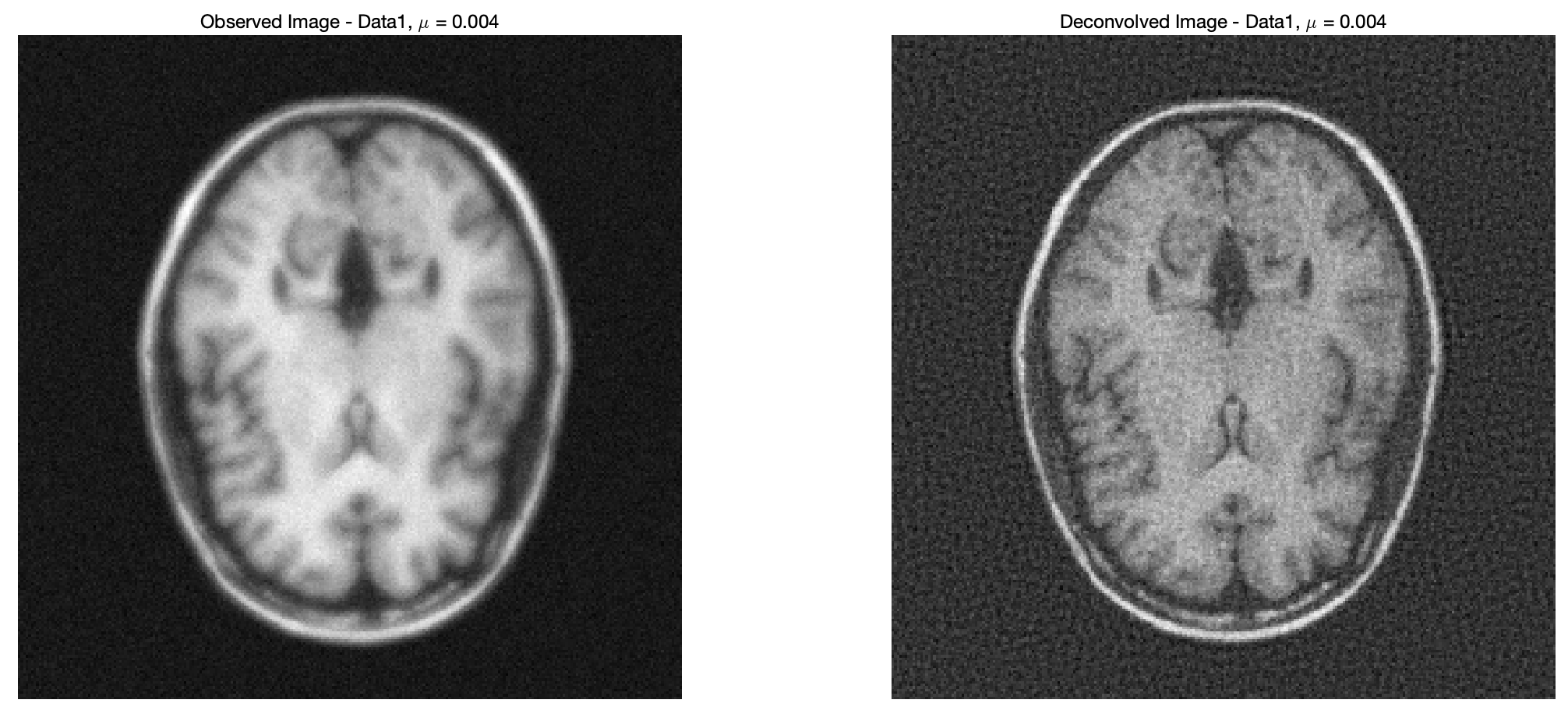
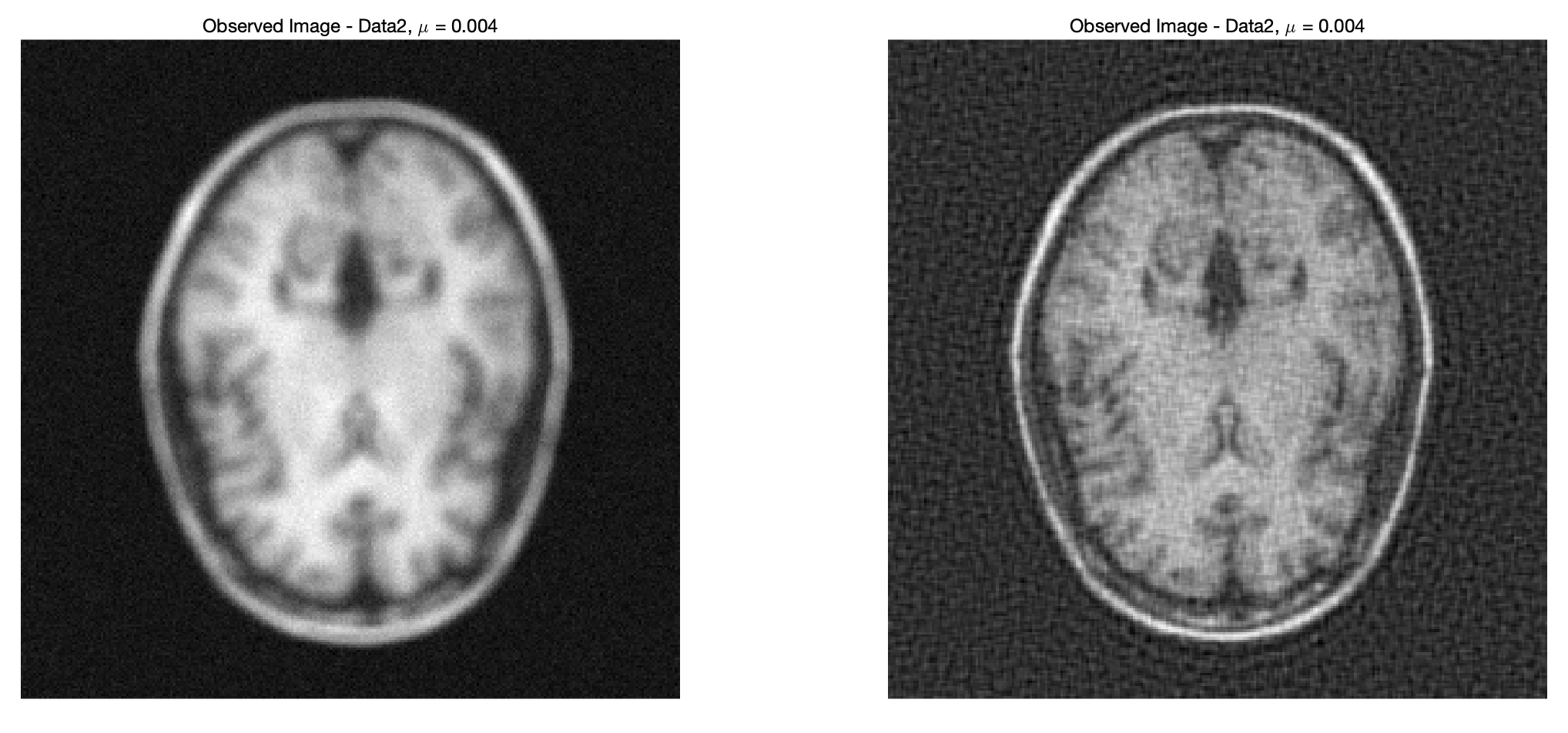
可见效果挺理想,但是之前这个 \mu 是随便设的,现在探讨这个 \mu 值对结果的影响。
首先考虑简单的逆滤波器情况,即 \mu = 0 。
前面我们得到:
现在变成:
因此:
%% Question 6 Simple Inverse Filter (μ = 0)
mu = 0;
% Deconvolve Data1
x_1 = deconvolve_image(Data1.Data, Data1.IR, mu);
% Display the deconvolved image
figure;
subplot(1,2,1)
% Display the image, grayscale
imagesc(Data1.Data);
colormap('gray');
% Scale the axes and eliminate the grading
axis('square','off')
title(['Observed Image - Data1, \mu = ', num2str(mu)]);
subplot(1,2,2)
imagesc(x_1);
colormap('gray');
title(['Deconvolved Image - Data1, \mu = ', num2str(mu)]);
axis('square','off')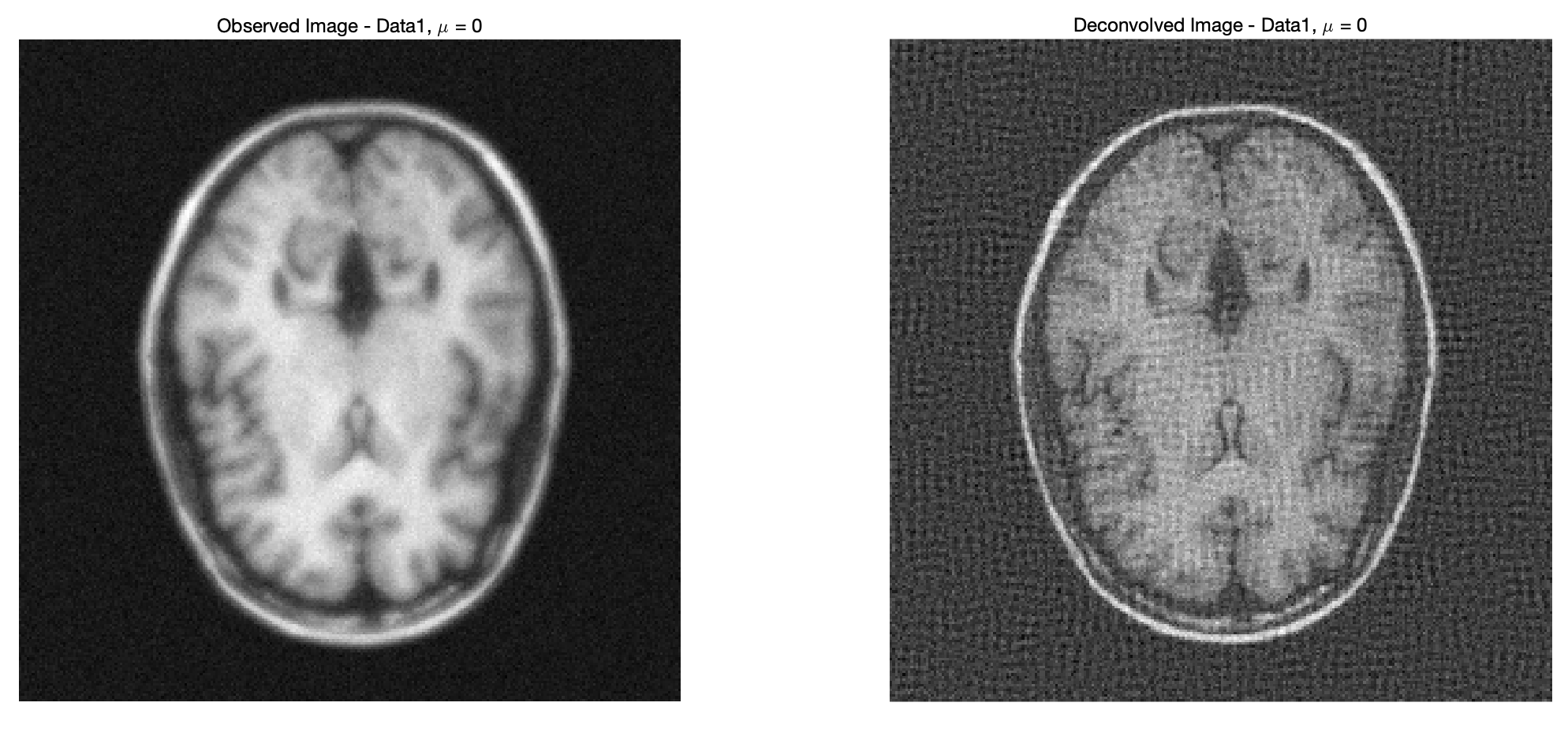
由于\mu = 0 等价于丢失了正则化项,反卷积结果会直接依赖于卷积核H 的傅里叶系数|\hat{H}(\nu_{x}, \nu_{y})|^2,如果H 的某些频率分量(尤其是高频)接近零,那么在这些频率上,分母|\hat{H}(\nu_{x}, \nu_{y})|^2 会非常小,导致反卷积结果中放大这些频率分量的噪声。反卷积图像中可以看到明显的颗粒状噪声。这是由于直接逆滤波在某些频率分量上产生了极大值,放大了噪声。
% Deconvolve Data2
x_2 = deconvolve_image(Data2.Data, Data2.IR, mu);
% Display the deconvolved image
figure;
subplot(1,2,1)
% Display the image, grayscale
imagesc(Data2.Data);
colormap('gray');
% Scale the axes and eliminate the grading
axis('square','off')
title(['Observed Image - Data2, \mu = ', num2str(mu)]);
subplot(1,2,2)
imagesc(x_2);
colormap('gray');
title(['Observed Image - Data2, \mu = ', num2str(mu)]);
axis('square','off')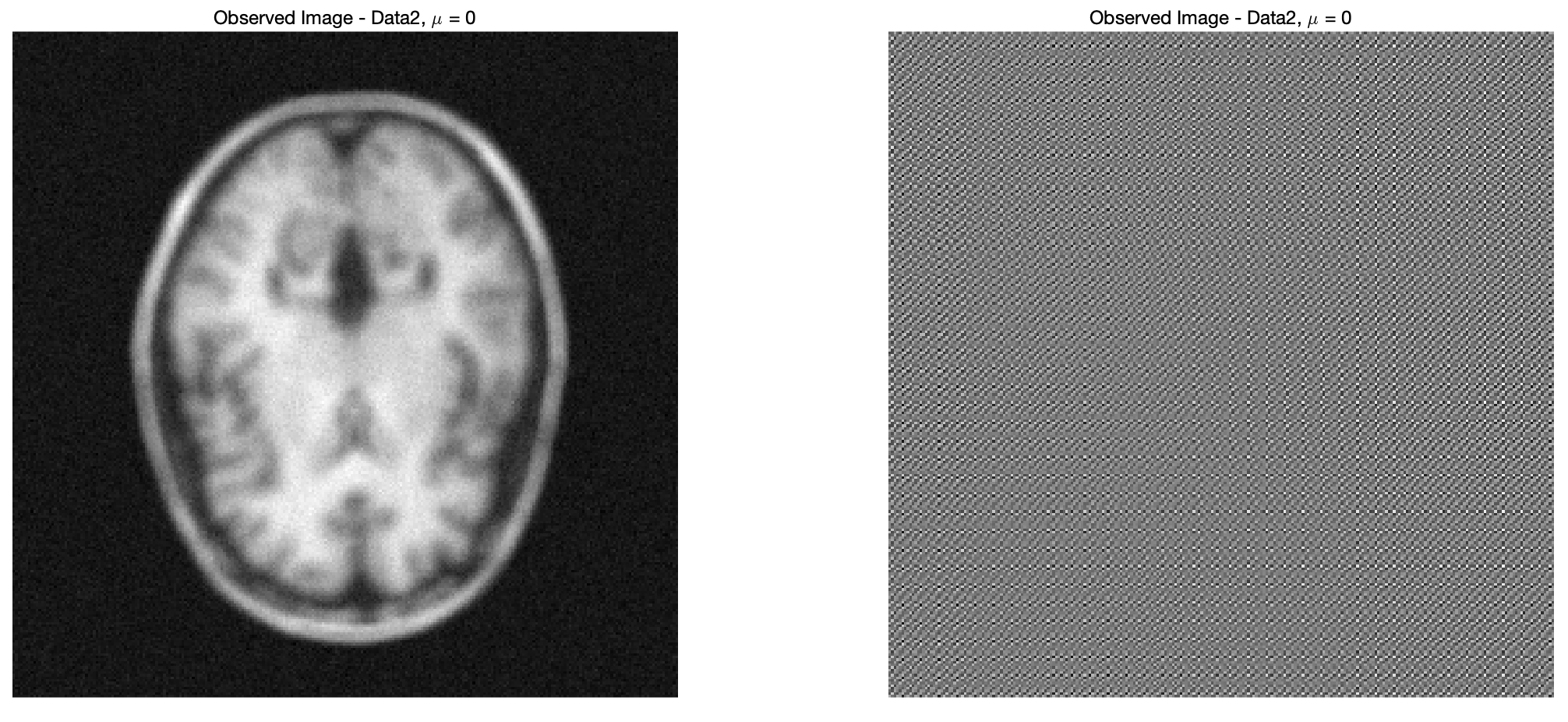
我们因此取不同的\mu 值(在\log_{10} 刻度上取值)。并且根据结果,确定合适的\mu 值。
%% Effect of Varying μ on Deconvolution Results
% Define a range of mu values on a log scale
mu_values = logspace(-11, 0, 12); % From 1e-10 to 1
% Deconvolution and display for Data1
figure('Name', 'Deconvolution Results for Data1');
for i = 1:length(mu_values)
mu = mu_values(i);
x_1 = deconvolve_image(Data1.Data, Data1.IR, mu);
subplot(3,4,i);
imagesc(x_1);
colormap('gray');
axis('square','off');
title(['\mu = ', num2str(mu, '%.1e')]);
end
sgtitle('Deconvolved Images - Data1 with Different \mu Values');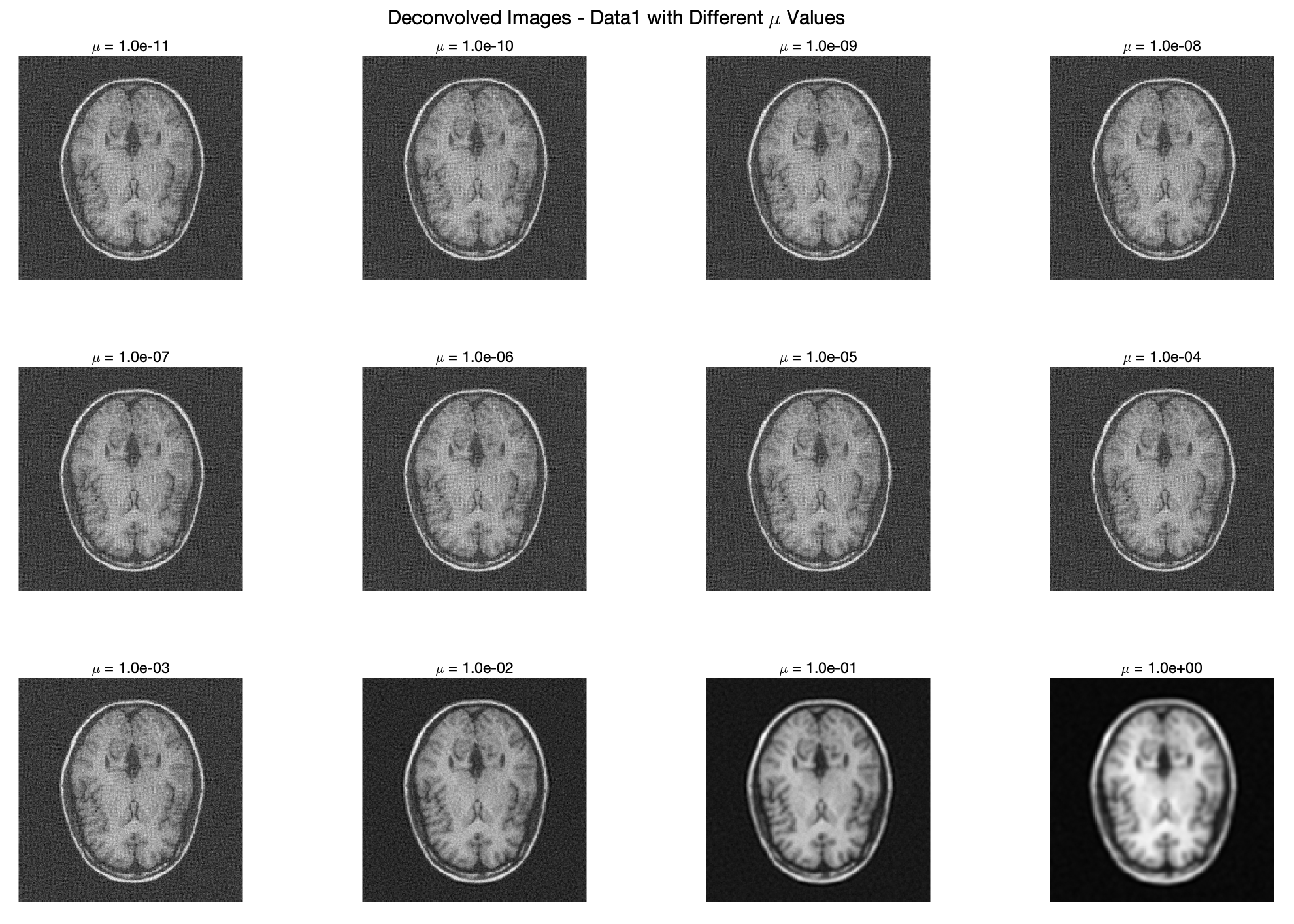
% Deconvolution and display for Data2
figure('Name', 'Deconvolution Results for Data2');
for i = 1:length(mu_values)
mu = mu_values(i);
x_2 = deconvolve_image(Data2.Data, Data2.IR, mu);
subplot(3,4,i);
imagesc(x_2);
colormap('gray');
axis('square','off');
title(['\mu = ', num2str(mu, '%.1e')]);
end
sgtitle('Deconvolved Images - Data2 with Different \mu Values');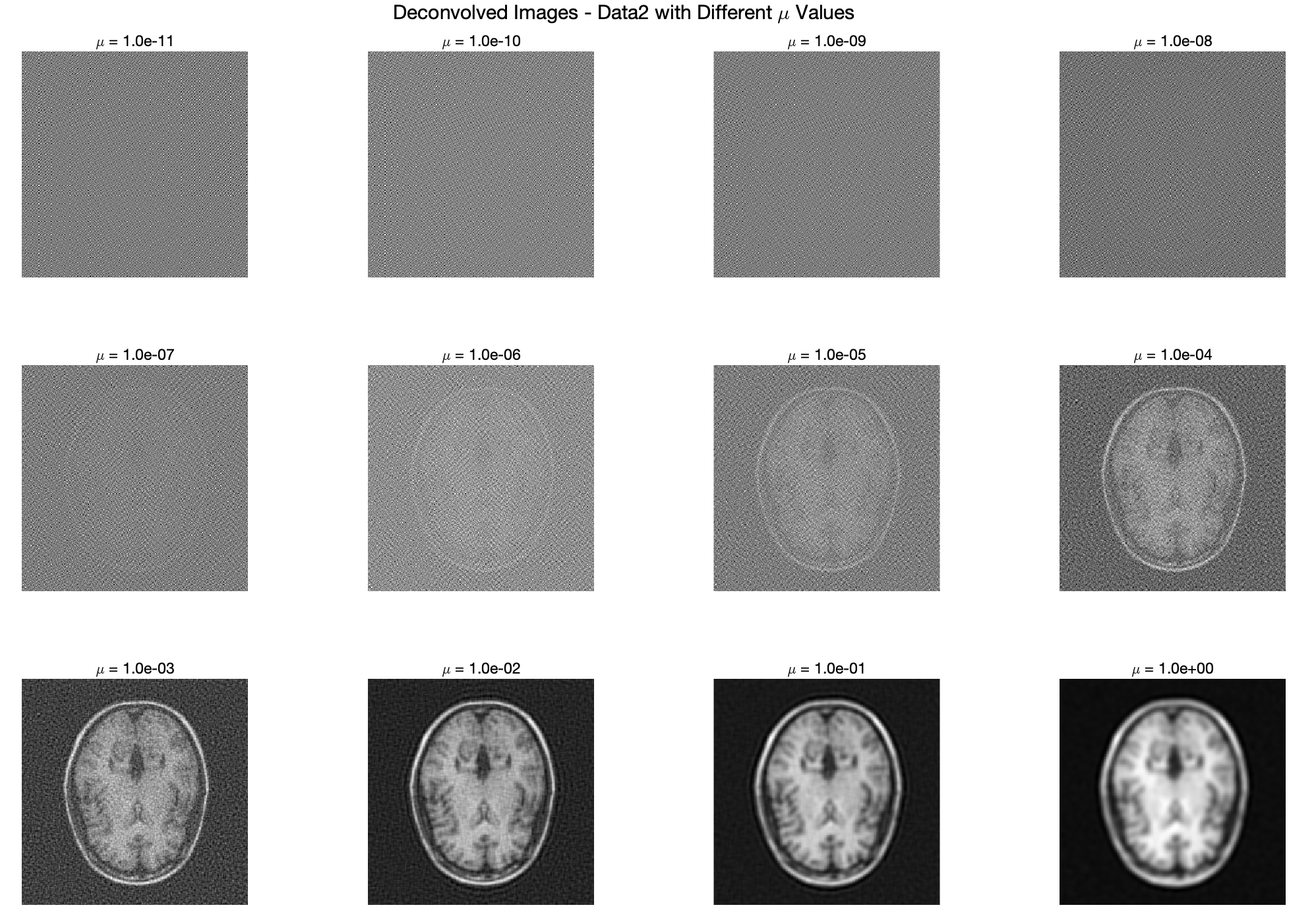
小的\mu 值时,可见图像噪声多,甚至都有可能完全被噪声埋没;中等\mu 值时,图像细节和噪声之间达到了较好的平衡;当\mu 值过大时,图像变得过于平滑,细节逐渐丢失,尤其是当\mu = 1 时。我们目前只能通过视觉方法来选出较好的\mu 值,两数据最优\mu 值都大约等于0.01,但是这样肯定是不行的,是不严谨的,是无法成为一名科研奇才的,因此我们和真实图像做数学比较。
2.4 超参数的作用
上一点使我们能够评估与反卷积问题相关的内在难度。它还表明,考虑重建图像期望正则性的先验信息可以获得更好的结果。这种方法因此使我们能够在两种信息源之间进行折衷:观测数据和可用的先验信息(关于正则性)。这是通过参数\mu 的值来实现的。在下面的研究中,选择一个最合适的\mu 值,以使反卷积图像既不过于平滑也不过于不规则。
因此,可以计算反卷积图像\hat{x} 和真实图像x^\star 之间的数值差异,作为正则化参数\mu 的函数。
为此,考虑以下三种距离函数:
当恢复的图像类似于真实图像时,这些距离接近于0,当恢复的图像为零时,它们接近1。
我们设定\mu 值在10^{-10} 和10^{10} 之间取对数间隔值。
%% Question 8
% Load TrueImage (focus on Data2)
TrueImage = Data2.TrueImage;
mu=logspace(-10, 10, 100);
for i=1:length(mu)
val_mu=mu(i);
% Deconvolve image with current mu
x_hat_temp = deconvolve_image(Data2.Data, Data2.IR, val_mu);
delta_2(i)=norm(x_hat_temp-TrueImage,2)/norm(TrueImage,2);
delta_1(i)=norm(x_hat_temp-TrueImage,1)/norm(TrueImage,1);
delta_inf(i)=norm(x_hat_temp-TrueImage,Inf)/norm(TrueImage,Inf);
end
% Find mu that minimizes each distance
[min_delta_2,ind_min_delta_2]=min(delta_2);
[min_delta_1,ind_min_delta_1]=min(delta_1);
[min_delta_inf,ind_min_delta_inf]=min(delta_inf);
mu_min_delta_2 = mu(ind_min_delta_2);
mu_min_delta_1 = mu(ind_min_delta_1);
mu_min_delta_inf = mu(ind_min_delta_inf);
% Display the results
fprintf('Delta_2 的最小值为: %e,对应的 mu 为: %e\n', min_delta_2, mu_min_delta_2);
fprintf('Delta_1 的最小值为: %e,对应的 mu 为: %e\n', min_delta_1, mu_min_delta_1);
fprintf('Delta_inf 的最小值为: %e,对应的 mu 为: %e\n', min_delta_inf, mu_min_delta_inf);
% Plot the distances as functions of mu
figure;
subplot(3,1,1)
loglog(mu, delta_2, 'b-', 'LineWidth', 2);
hold on;
loglog(mu(ind_min_delta_2), min_delta_2, 'ro', 'MarkerSize', 8, 'LineWidth', 2);
xlabel('\mu');
ylabel('\Delta_2(\mu)');
title('\Delta_2 vs \mu');
grid on;
legend('\Delta_2(\mu)', ['Min at \mu = ', num2str(mu_min_delta_2, '%.1e')]);
subplot(3,1,2)
loglog(mu, delta_1, 'g-', 'LineWidth', 2);
hold on;
loglog(mu(ind_min_delta_1), min_delta_1, 'ro', 'MarkerSize', 8, 'LineWidth', 2);
xlabel('\mu');
ylabel('\Delta_1(\mu)');
title('\Delta_1 vs \mu');
grid on;
legend('\Delta_1(\mu)', ['Min at \mu = ', num2str(mu_min_delta_1, '%.1e')]);
subplot(3,1,3)
loglog(mu, delta_inf, 'm-', 'LineWidth', 2);
hold on;
loglog(mu(ind_min_delta_inf), min_delta_inf, 'ro', 'MarkerSize', 8, 'LineWidth', 2);
xlabel('\mu');
ylabel('\Delta_\infty(\mu)');
title('\Delta_\infty vs \mu');
grid on;
legend('\Delta_\infty(\mu)', ['Min at \mu = ', num2str(mu_min_delta_inf, '%.1e')]);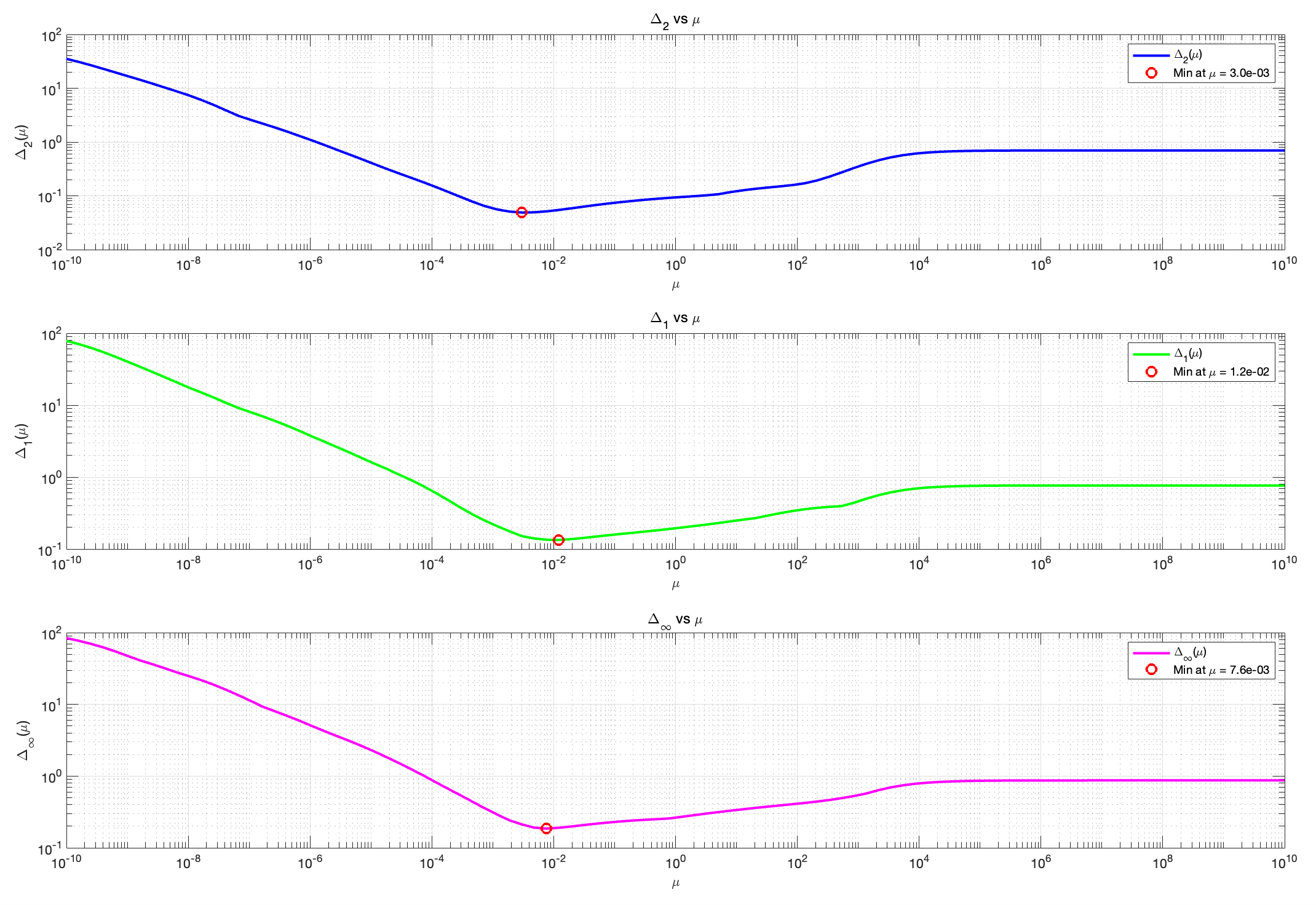
Delta_2 的最小值为: 4.887066e-02,对应的 mu 为: 2.983647e-03
Delta_1 的最小值为: 1.337040e-01,对应的 mu 为: 1.204504e-02
Delta_inf 的最小值为: 1.855954e-01,对应的 mu 为: 7.564633e-03和之前肉眼观察得到的 \mu 值相比,可见差距还是挺大的。