反问题: 基于Gibbs采样的贝叶斯自适应调参方法
编辑在上一个实践内容中,我们介绍了去卷积问题的困难,即在应用卷积或者低通滤波器后所导致的观测数据缺失高频相关信息的情况。我们使用了 Wiener-Hunt 方法:将量化解的误差的二次项和数据相结合,并在损失函数中使用带有正则化系数的二次惩罚标准以量化解的粗糙度。我们得到了相对来说不错的结果。但是这个方法的缺点是它需要调节一个参数,即正则化参数 \mu。我们最开始由经验选择到观察选择,一直到最后循环找到 \mu 的最优值,使得去卷积后的图像既不过于不规则也不过于平滑。下面的工作重点在于介绍一种自动调节超参数的方法。
1. 超参数与全后验分布
这个方法基于 Wiener-Hunt 解的贝叶斯解释。该解释本身基于关于误差 e 和关于图像 x 的两个高斯概率模型。
1.1 误差分布
误差被建模为白色、零均值同质高斯向量。白色指的是像白噪音一样,在其频谱特性中,所有频率分量有相同的功率密度,即信号在不同频率上的能量分布是均匀的,在数学层面,它具有零相关性,即不同时间点的误差值是统计独立的(不相关的)。
对于高斯分布,选择了一个涉及所谓精度参数 \gamma_e(方差的倒数)的替代参数化。根据这种参数化,其表达式可写为:
根据 y = Hx + e,数据 y 和感兴趣信号 x 的似然函数表达式:
根据所给的似然表达式 f(y \mid x, \gamma_e),量化重建物体 x 相对于观测数据 y 的充分性可以通过协对数(log-likelihood)的形式表示。这种表达经常用于概率模型中,特别是最大似然估计(MLE)或贝叶斯推断中,用于评估模型参数的适配程度。
再补充一下协对数相关内容,就是似然函数取对数,对于上述似然函数表达式,取其对数后为:
利用对数的性质:\ln(a \cdot b) = \ln a + \ln b,将三部分拆分开:
逐项计算:
合并得到:
回到之前的内容,我们使用了协对数来表达数据能否充分重建原信号,我们给出这种拟合程度的量化指标:
|y - Hx|^2 是重建信号(模型参数x)与观测数据y 的误差平方和,称为残差平方和(Residual Sum of Squares, RSS)。
-k_y \log f(y \mid x, \gamma_e) 是协对数的负加权形式,其中k_y > 0,是一个常数。
C_y 也是一个常数。
我们现在给出两个常数k_y 和C_y 的对应表达式:
前面得到:
将上述结果带入 \mathcal{J}_{LS}(x) = -k_y \log f(y \mid x, \gamma_e) + C_y 得:
将上述结果和原公式 \mathcal{J}_{LS}(x) = |y - Hx|^2 做对比得到结果:
1.2 感兴趣信号的分布
贝叶斯解释要求为感兴趣的信号 x 提供一个概率分布。其模型也是高斯分布,只是这里它不是白色的,也就是说,它的各组成部分之间存在相关性。在接下来的内容中,相关性实际上是通过协方差矩阵 R 来建模的。
贝叶斯解释的核心思想是为感兴趣的信号 x 提供一个概率分布,而不是一个确定值。这种概率分布反映了我们对 x 的不确定性以及其任何可能的取值。因此我们假设在模型中,x 服从一个高斯分布。
但是它是一个非白色的高斯分布,也就是它的各组成部分之间存在相关性,协方差矩阵 R 是一个非对角矩阵,其非零非对角元素表示信号的不同分量之间的相关性。后续我们就使用这个协方差矩阵 R 在贝叶斯框架中建模信号的相关性。
补充一下关于协方差矩阵的相关内容
协方差矩阵 R 提供了对信号相关性的精确描述。元素 R_{ij} 表示信号第 i 和第 j 个分量之间的协方差:
根据相关性,R 可能是一个稀疏矩阵或者满矩阵。
在贝叶斯建模中:
1. 信号 x 的 先验 分布 p(x) 使用协方差矩阵 R 的描述公式为:
其中,R^{-1} 是协方差矩阵的逆,也称为精度矩阵,定义了 x 的相关性强度。
2. 最大后验估计(MAP):
利用先验分布p(x) 和观测数据y 的似然函数p(y \mid x),可以通过贝叶斯法则计算x 的后验概率分布p(x \mid y),并基于该分布选择最优解。
回到之前,我们通过逆矩阵R^{-1} = \gamma_x \Pi 来表示建模信号的相关性,其中:
精度参数\gamma_x 控制相关性的强度
矩阵\Pi 决定了相关性的结构
我们将R^{-1} = \gamma_x \Pi 带入之前的f(x \mid \gamma_x) 公式可得:
也就是说:
量化物体相对于先验信息充分性的项表现为密度的协对数:
其中:
\mathcal{J}_0(x) 是对信号x 的量化,用来描述x 相对于先验信息(即对x 的已知假设或统计特性)是否充分匹配。其形式以密度的协对数(具体是取对数的负数)表示,结合了贝叶斯模型中的先验分布。
f(x \mid \gamma_x) 是x 的先验概率密度函数,反映了x 如何符合假设的先验模型,我们之前在假设x 服从高斯分布的前提下,得到了其表达式(见上面)。
正则化项x^T \Pi x 描述了信号x 的“复杂度”或“平滑性”,由\Pi 决定其结构,精度参数\gamma_x 控制正则化的强度,当\gamma_x 较大时,正则化约束更强。
同样,在上述公式中,我们添加了加法常数C_x 和乘法常数k_x。为了与之前已经计算过的 Wiener-Hunt 方法联系起来,只需选择\Pi = D^T D。
现在我们要给出两个常数的对应表达式。
已知原公式:
两边取对数:
根据公式:
将上述结果带入其中得到:
对比:
得到:
但是严格来说,上述解释并不完全正确,因为D^T D。常量图像只不过是对应于特征值为零的特征向量(这对应于零频率)。严格的发展要求引入一个用于零频率下能量的惩罚项(通过一个可以设定为任意小值的参数)。不懂,后面补充。
上面提到的这个f(x \mid \gamma_x) = (2\pi)^{-N/2} \det(\Pi)^{1/2} \gamma_x^{N/2} \exp\left( -\frac{\gamma_x x^T \Pi x}{2} \right) 先验分布(a priori),因为它使人们能够处理先验信息,从而更倾向于具有更高规则性的图像。对于给定图像的概率越高,则图像越规则。
其中的\gamma_x 精度参数我们非常关注,因为它控制着图像的平滑度,进而影响着概率分布的整体趋势。
当\gamma_x 较大时,指数项中的x^T \Pi x 会被放大。
当\gamma_x 较小时,指数项中的x^T \Pi x 对总的概率密度的影响较小。待补充。
1.3 后验分布
借助前面定义的两个成分,并使用概率的乘法规则,现在可以构造重构信号 x 和数据 y 的联合密度:
将之前得到的结果代入:
这个表达式由两个精度参数 \gamma_e 和 \gamma_x 参数化。可以注意到在指数项内部,我们得到了加权最小二乘准则的表达式:
其中,正则化参数 \mu 表示为信噪比的倒数 \mu = \gamma_x / \gamma_e。正则化参数 \mu 在 \gamma_e 和 \gamma_x 中的作用是?
待补充
通过贝叶斯定理可以确定感兴趣信号的后验分布(后验概率分布):
这就是给定数据(已观测到的)和参数下的感兴趣信号的分布。
我们希望为感兴趣信号构造的任何估计器都基于上述分布。最常见的估计器是后验分布的均值、中位数或众数(即后验的最大化者)。在当前情况下,当后验分布是高斯分布时,这三者是相等的。众数或后验最大化者(MAP),记为 \hat{x} {MAP} 。也就是最小化准则 \mathcal{J} {PLS}(x) 的解
结论是,最小二乘准则的解\hat{x}_{MAP} 就是之前的工作中推导出来的后验分布的众数\hat{x}_{MAP}。
1.4 扩展的后验分布
到目前为止,贝叶斯方法只允许我们对已经存在的超参数值的估计给出概率解释。将之前的框架扩展到包含超参数的估计,需要为两个精度参数\gamma_e 和\gamma_x 引入一个先验分布。在多种可选方案中,接下来我们将重点关注伽马分布:
它由两个正实数参数(\alpha, \beta) 驱动,具有均值\alpha / \beta 和方差\alpha / \beta^2。这种选择的理由如下:
选择伽马分布作为先验分布确保了条件后验分布也是伽马分布(我们正在讨论共轭先验)。在算法上,这意味着只需要更新分布参数的值(具体见下面)。
这种选择允许在参数值的信息较少(也称为“非信息先验”)或精确(如名义值或某种不确定性)的情况下进行处理。该工作中特别感兴趣的是“非信息先验”的极限情况,即(\alpha, \beta) = (0, 0)。
此外,关于变量\gamma_e 和\gamma_x 的组合,它们被建模为独立的。
从伽马分布:
和部分联合分布:
我们推导出对于 y, x, \gamma_e 和 \gamma_x 的完整联合分布的表达式为:
其明确表达为:
注意:这个密度非常重要,因为它允许推导出所有相关的联合、边缘和条件密度。
现在我们可以通过贝叶斯规则推导出完整的后验分布,即给定观测数据y 时,感兴趣信号x 和超参数\gamma_e,\gamma_x 的分布:
这汇总了所有关于感兴趣信号和超参数在数据视角下的可用信息:对于三重项x,\gamma_e,\gamma_x,它量化了后验密度,即在给定观测数据下三重项的概率。感兴趣信号和超参数的估计器是从这个分布中构造出来的。我们可以查看后验分布的均值、中位数或众数。每种方法都有其优缺点。在接下来的内容中,我们将重点讨论均值。
1.5 后验均值
考虑到后验分布(上面这个)的复杂性,获得均值的解析公式是不可行的。为了计算后验均值,有几种方法可用,在这里我们将重点关注随机采样技术。最终,它归结为对后验分布进行随机采样,然后取样本的经验均值,从而近似后验均值。
后验分布的采样可以通过马尔可夫链蒙特卡洛(MCMC)方法来实现。它要求构建一个迭代过程,以生成随机样本,经过一定的时间(称为 burn-in),这些样本将根据目标分布进行分布。构建这样一个过程并不容易,但在当前情况下,存在一个标准算法可以轻松使用:Gibbs 采样算法。它将对三重项x,\gamma_e,\gamma_x 的后验分布进行采样的问题,转换为它们三个各自的更简单分布的采样问题。每个分布实际上是条件分布,给定其余参数的条件下对其中一个参数进行采样。该算法的工作原理在下表中给出,接下来的部分我们将详细说明这些步骤。
1.5.1 采样逆误差功率
采样对应于步骤 (a) 的超参数\gamma_e 需要从条件后验分布f(\gamma_e | x, \gamma_x, y) 中采样。该分布由完整的联合分布f(x, y, \gamma_e, \gamma_x) 获得,如下所示:
仅保留包含\gamma_e 的项(与\gamma_e 相关的部分),并且由于分母不依赖于\gamma_e,我们得到:
由此获得的条件分布实际上是具有参数(\alpha, \beta) 的伽马分布:
在先验参数(\alpha_e, \beta_e) 等于(0, 0) 的极限情况下,后验的参数为:
因此我们关注于这个f(\gamma_e | x, \gamma_x, y) 分布的均值和方差表达式,并将它与输出误差y - Hx 的功率相关联。
已知伽马分布的概率密度函数:
其中: \alpha 是形状参数, \beta 是尺度参数。
对于伽马分布 \text{Gamma}(\alpha, \beta) ,其均值和方差的标准表达式分别为:
均值:
方差:
已知:
误差精度参数 \gamma_e 的均值:
误差精度参数 \gamma_e 的方差:
伽马分布中的\beta 参数直接依赖于\| y - Hx \|^2。
当误差\| y - Hx \|^2 较大时,\beta参数也会增大,表示模型拟合较差,这意味着伽马分布的均值和方差会减小,反映了误差增加时对数据的信任度降低。
反之,误差\| y - Hx \|^2 较小时,精度参数\gamma_e 的均值增大,表示对数据的信任度较高。
因此为了实现步骤 (a):\gamma_e^{[k]}的样本从具有上述两个参数\alpha 和\beta 的伽马分布中抽取,我们可以使用 Matlab 中的 RNDGamma(Alpha, Beta); 函数,具体代码为:
function SamplePrecision = RNDGamma(Alpha,Beta)
% The Precision variable is a sample of the gamma distribution with parameters Alpha and Beta
% Tirage d'un échantillon Gamma approché par du Gauss (JFG+TBC)
SamplePrecision = Alpha/Beta + sqrt( Alpha/(Beta*Beta) ) * randn;注意:计算参数\beta 涉及计算建模误差\| y - Hx \|^2 的范数。计算空间域中的范数通常成本较高,但是可以在傅里叶域中进行计算以降低成本。
1.5.2 采样感兴趣信号的逆功率
现在我们将重点放在采样超参数\gamma_x 上,对应于表 1 中算法的步骤 (b)。
这需要采样条件后验分布f(\gamma_x | x, \gamma_e, y)。使用与上一节类似的方法,我们得到:
可以看出,这个条件后验分布也是伽马分布。在先验参数(\alpha_x, \beta_x) 等于(0, 0) 的极限情况下,后验参数为:
因此我们关注于f(\gamma_x | x, \gamma_e, y) 这个分布的均值和方差表达式,并将它与输出误差y - Hx 的功率相关联。
均值:
方差:
当图像x 的二次形式较小时(即图像较为平滑),均值会相应增大。这表明我们更信任较为平滑的图像。
因此为了实现步骤 (b)\gamma_x^{[k]} 的样本从具有上述两个参数的伽马分布中抽取,同样使用 RNDGamma 函数。
注意:计算参数\beta 涉及计算建模误差\| y - Hx \|^2 的范数。计算空间域中的范数通常成本较高,但是可以在傅里叶域中进行计算以降低成本。
1.6 采样感兴趣的物体
最后但同样重要的是,我们将处理对应于表 1 中算法步骤 (c) 的感兴趣物体x 的采样。这意味着采样条件后验分布f(x | \gamma_x, \gamma_e, y),其表达式已经推导出。
并且它便捷地重新写为:
该密度本身是高斯分布,因为指数项内的变量x 是正定的二次项。它由均值和协方差矩阵完全表征。在这种情况下:
均值\mu_{x|*} 也是众数,作为最小化\mathcal{J}_{PLS}(x) 的解,即之前实践工作中讨论的 Wiener-Hunt 解。
协方差矩阵\Sigma_{x|*} 通过计算\mathcal{J}_{PLS}(x) 的 Hessian(即二阶导数矩阵)获得。
我们得到以下表达式:
当前面临的数值问题是对可能具有高维的高斯分布进行采样。这个高维度性阻止了协方差矩阵 \Sigma_{x|*} 的求逆或分解,这意味着没有简单的采样方案可用。为了解决这个问题,我们采用循环矩阵的近似方法,从而能够在傅里叶域中进行快速的矩阵运算。给出了以下表达式:
在傅里叶域中,协方差矩阵是对角线形式的,这意味着其各个分量是解相关的。因此,每个分量是独立的,这使得可以并行采样。
接下来我们给出上面两个表达式的推导过程,基于循环矩阵对角化的思想。
由于矩阵H 是实数矩阵,因此它也是它的复共轭矩阵,且H^t = H^\dagger。$D$ 同理。
因此我们将利用循环矩阵的对角化性质,由于H 和D 是循环矩阵,且循环矩阵是具有特殊结构的方阵,矩阵的每一行元素是前一行元素循环右移一位。基于这一性质,循环矩阵的一个重要性质是,它可以通过傅里叶变换对角化。具体来说,任何N \times N 的循环矩阵C 都可以写成:
F 是离散傅里叶变换矩阵,F^\dagger是其共轭转置(逆傅里叶变换)。
\Lambda 是一个对角矩阵,其元素为矩阵C 的特征值(傅里叶系数)。
之前我们得到的方程为:
我们的目标是利用循环矩阵的性质将其转换到频域,从而得到新的表达式。先将 H 和 D 对角化:
带入原方程:
将 F 和 F^\dagger 提到外面:
第一个公式证明完毕:
回到开始,我们有:
把上述公式带入原方程:
计算得:
由于 F^\dagger F = I,可以简化为:
第二个公式证毕。
在进行步骤 (c) 时,对图像 x^{[k]} 的样本应从具有在傅里叶域中给定的第一和第二矩中的高斯分布中抽取。可以使用自定义的 Matlab 函数 RNDGauss(Moy, Cov),Moy 和 Cov 必须在傅里叶域中给出,函数具体内容为:
function SampleImage = RNDGauss(MoyGauss,Covariance)
% Generate an image sample under a Gaussian distribution, with the mean given by Moy and the covariance given by Cov.
% The parameters Moy and Cov, and Image, are all in the Fourier domain, not in the spatial domain.
% Paramètre de Taille
Taille = length(MoyGauss);
% Tirage d'un bruit blanc avec la bonne symétrie
BoutGauss = randn(Taille,Taille) + sqrt(-1) * randn(Taille,Taille);
BoutGauss = MyFFT2( real( MyIFFT2(BoutGauss) ) );
% Filtrage du bruit blanc
SampleImage = MoyGauss + BoutGauss .* sqrt(Covariance);2 实现
在 Matlab 实践中,我们使用和上次内容相同的数据集,最后结果理论上应该相似。因为我们做出的改进只是自动调整正则化参数。我们之前介绍了算法步骤,并且详细解释了涉及两个超参数 \gamma_e 和 \gamma_x 的条件分布采样,以及图像 x 的条件分布采样,所以这里直接给代码。
clear all
close all
clc
%% 加载数据 (与TP1保持一致)
Data1 = load('DataOne.mat'); % 包含Data, TrueImage, IR
Data = Data1.Data;
TrueImage = Data1.TrueImage;
IR = Data1.IR;
[M,N] = size(Data);
%% 构建频域传递函数 (与TP1一致)
Long = length(Data); % 假设Data为方阵
H = MyFFT2RI(IR,Long);
% 构建正则化滤波器频域 (Dh,Dv) 与 TP1中介绍的 D 矩阵类似
Dh = [0 0 0;0 -1 1;0 0 0];
Dv = [0 0 0;0 -1 0;0 1 0];
F_Dh = MyFFT2RI(Dh, Long);
F_Dv = MyFFT2RI(Dv, Long);
abs_D_squared = abs(F_Dh).^2 + abs(F_Dv).^2;
Y = MyFFT2(Data);
%% 超参数先验 (无信息先验)
alpha_e = 0; beta_e = 0;
alpha_x = 0; beta_x = 0;
% 初始化参数
x = Data; % 初始化x为观测图像
gamma_e = 1; % 初始化误差精度参数
gamma_x = 1; % 初始化信号精度参数
numIter = 500; % MCMC迭代次数,可根据实际需要调整
burnIn = 200; % burn-in期长度
X_samples = zeros(M,N,numIter);
gamma_e_samples = zeros(numIter,1);
gamma_x_samples = zeros(numIter,1);
%% MCMC (Gibbs) 迭代
for k = 1:numIter
% ---- (a) 更新gamma_e ----
% 残差计算:r = y - Hx
r = Data - MyIFFT2( H .* MyFFT2(x) );
norm_r2 = sum(abs(r(:)).^2);
alpha_e_post = alpha_e + (M*N)/2;
beta_e_post = beta_e + norm_r2/2;
% 使用自定义RNDGamma函数(请确保RNDGamma.m未修改)
gamma_e = RNDGamma(alpha_e_post, beta_e_post);
% ---- (b) 更新gamma_x ----
% 计算 x^T Pi x 的值:在频域中为 sum(|X|^2 * |D|^2)
Xf = MyFFT2(x);
norm_x_Pi2 = sum(abs(Xf(:)).^2 .* abs_D_squared(:));
alpha_x_post = alpha_x + (M*N)/2;
beta_x_post = beta_x + norm_x_Pi2/2;
% 使用自定义RNDGamma函数
gamma_x = RNDGamma(alpha_x_post, beta_x_post);
% ---- (c) 更新x ----
% 协方差的对角阵(频域):var_x_f = 1 / (gamma_e|H|^2 + gamma_x|D|^2)
denom = gamma_e*(abs(H).^2) + gamma_x*(abs_D_squared);
% 均值: MU_freq = (gamma_e * conj(H).*Y)./denom
MU_freq = (gamma_e * conj(H) .* Y) ./ denom;
% 使用自定义RNDGauss函数进行高斯分布采样 (RNDGauss.m未修改)
% RNDGauss要求参数 (MoyGauss, Covariance),此处 Covariance = var_x_f
X_f_new = RNDGauss(MU_freq, 1./denom);
x = MyIFFT2(X_f_new);
X_samples(:,:,k) = x;
gamma_e_samples(k) = gamma_e;
gamma_x_samples(k) = gamma_x;
end
%% 后验均值计算(去掉burn-in部分)
x_posterior_mean = mean(X_samples(:,:,burnIn+1:end), 3);
% 每次迭代计算与真实图像的MSE
MSE_iterations = zeros(numIter,1);
for i=1:numIter
MSE_iterations(i) = mean((X_samples(:,:,i)-TrueImage).^2,'all');
end
% 找到MSE最小的迭代次序及对应MSE值
[best_mse, best_iter] = min(MSE_iterations);
% 计算最终后验均值与真实图像的评价指标
mse_val = mean((x_posterior_mean(:)-TrueImage(:)).^2);
psnr_val = 10*log10(max(TrueImage(:))^2 / mse_val);
%% 打印最优值信息
fprintf('在所有迭代中,MSE最小值为 %.3e,对应迭代次数为 %d\n', best_mse, best_iter);%% 绘图
figure('Name','结果','NumberTitle','off','Color','w');
% 使用subplot将观测图像、真实图像、恢复图像对比展示(2行2列布局)
subplot(1,3,1);
imagesc(Data); colormap gray; axis image off;
title('观测(模糊)图像','FontWeight','bold','FontSize',12);
subplot(1,3,2);
imagesc(TrueImage); colormap gray; axis image off;
title('真实图像','FontWeight','bold','FontSize',12);
subplot(1,3,3);
imagesc(abs(x_posterior_mean)); colormap gray; axis image off;
title({['恢复图像(后验均值)'],...
['MSE: ' num2str(mse_val, '%.3e') ', PSNR: ' num2str(psnr_val,'%.2f') ' dB']}, ...
'FontWeight','bold','FontSize',12);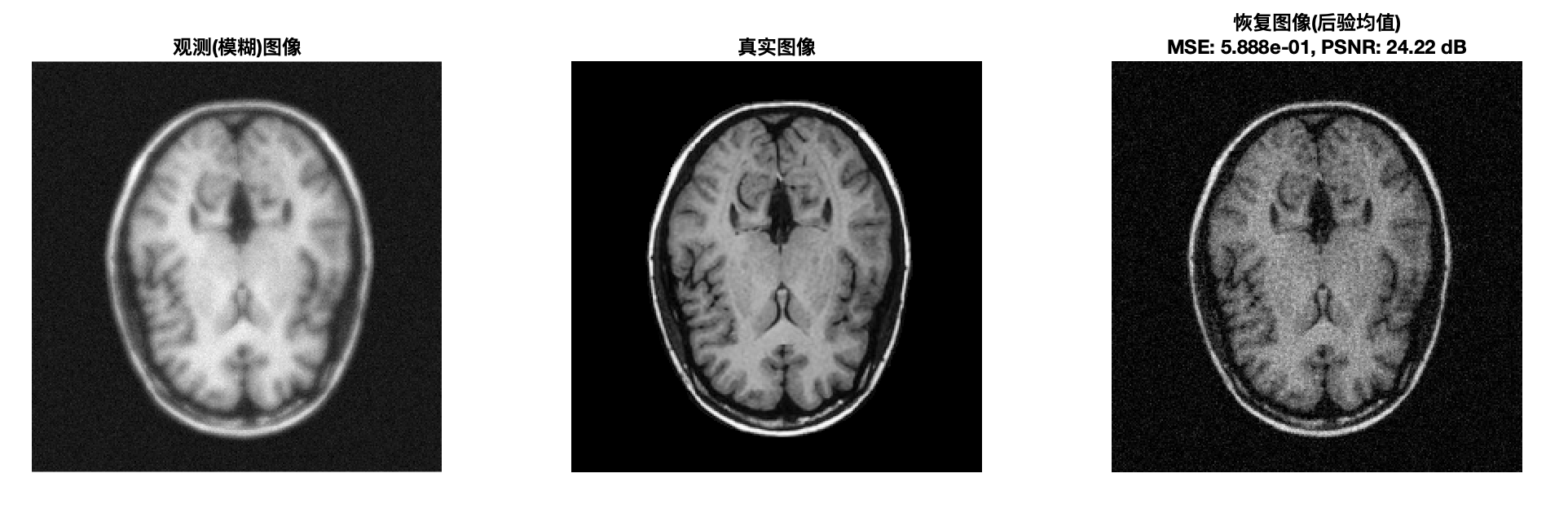
% 显示水平中心线处的像素值对比
figure('Name','截面对比','NumberTitle','off','Color','w');
mid_row = round(M/2);
plot(TrueImage(mid_row,:),'r-','LineWidth',2); hold on;
plot(x_posterior_mean(mid_row,:),'b--','LineWidth',2);
legend('真实图像','恢复图像','Location','best','FontSize',12);
xlabel('像素索引','FontWeight','bold','FontSize',12);
ylabel('像素值','FontWeight','bold','FontSize',12);
title('水平中心线像素截面比较','FontWeight','bold','FontSize',12);
grid on;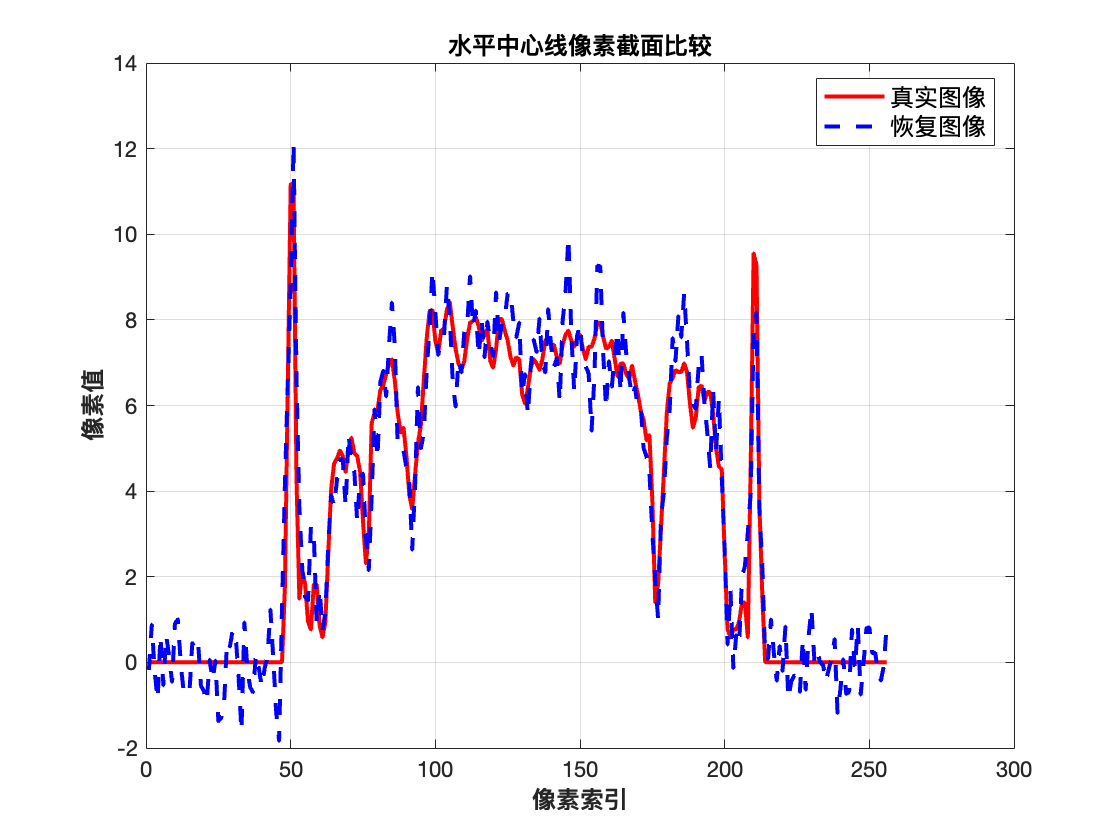
% 显示超参数迭代收敛情况
figure('Name','超参数收敛情况','NumberTitle','off','Color','w');
subplot(2,1,1);
plot(gamma_e_samples,'LineWidth',1.5);
xlabel('迭代次数','FontWeight','bold','FontSize',12);
ylabel('\gamma_e','FontWeight','bold','FontSize',12);
title('\gamma_e 的迭代变化','FontWeight','bold','FontSize',12); grid on;
subplot(2,1,2);
plot(gamma_x_samples,'LineWidth',1.5,'Color','m');
xlabel('迭代次数','FontWeight','bold','FontSize',12);
ylabel('\gamma_x','FontWeight','bold','FontSize',12);
title('\gamma_x 的迭代变化','FontWeight','bold','FontSize',12); grid on;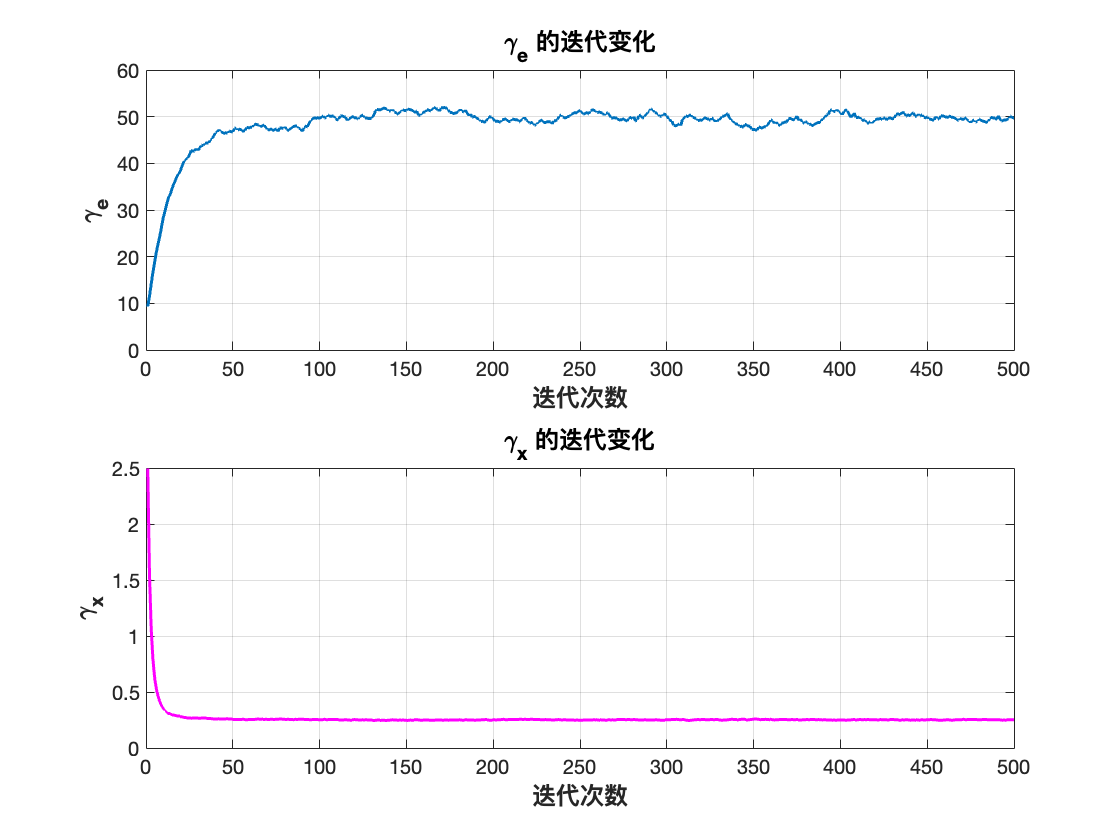
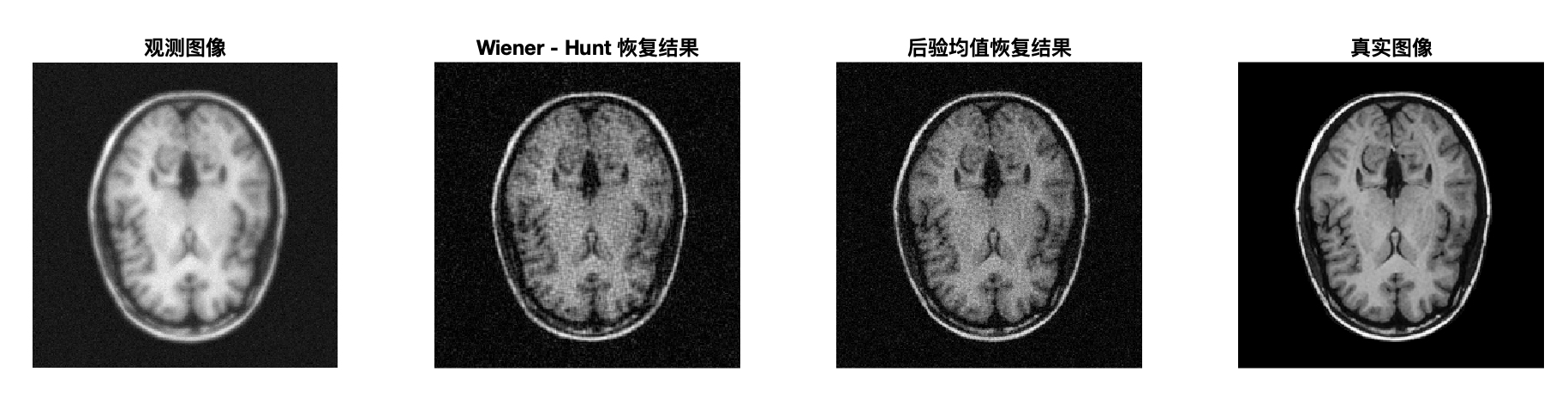
%% 对比展示:观测图像 vs 第一份结果 vs 本次恢复后验均值 vs 真实图像
load('x_first_method.mat','x_first_method');
figure('Name','最终对比展示','NumberTitle','off','Color','w');
subplot(1,4,1);
imagesc(Data); colormap gray; axis image off;
title('观测图像','FontWeight','bold','FontSize',12);
subplot(1,4,2);
% 假设 x_first_method 是从第一份内容中得到的恢复图像结果变量
% 请在运行此代码前确保 x_first_method 已经在工作区中存在
imagesc(abs(x_first_method)); colormap gray; axis image off;
title('Wiener - Hunt 恢复结果','FontWeight','bold','FontSize',12);
subplot(1,4,3);
imagesc(abs(x_posterior_mean)); colormap gray; axis image off;
title('后验均值恢复结果','FontWeight','bold','FontSize',12);
subplot(1,4,4);
imagesc(TrueImage); colormap gray; axis image off;
title('真实图像','FontWeight','bold','FontSize',12);