引言

本内容主要旨在实现图像合成、线性滤波、颜色分割和几何变换。

图像合成

目标： 合成一幅包含红、绿、蓝三个圆及其重叠部分的图像，以实现颜色的叠加。

计算三个圆的中心坐标 x_0 和 y_0，计算每个圆的掩码矩阵 V，并使用显式和隐式两种方法计算距离矩阵，验证了掩码的有效性。最后，提取每个圆的 RGB 通道，将其组合成一个 256 \times 256 \times 3 的 RGB 图像。

线性滤波

目标： 观察在应用不同滤波器的同时，图像在空间域和频率域中的变化，以理解这些滤波器对图像的影响，并将其应用于图像去噪。

首先使用低通滤波器来平滑图像，并观察其傅里叶变换，然后对图像进行去噪。首先使用均值、圆盘和高斯低通滤波器，我们发现它们无法消除特定频率的噪声，即滤波效果不佳。因此，使用带阻滤波器（在空间域中构建了一个由余弦函数调制的高斯滤波器）。

最后，应用高通滤波器来突出图像的边缘并提高其对比度。使用拉普拉斯算子 L 实现高通滤波。应用此高通滤波器 L 后，观察到图像的边缘被突出显示。然后，通过从原始图像中减去拉普拉斯滤波后的图像，从而实现对比度的增强。通过调整参数 \alpha，可以观察到对比度和边缘清晰度的变化。并且从空间域和频率域的角度解释这种操作如何改善图像。

颜色分割

目标： 通过颜色分割技术，根据参考颜色对图像进行分割，并将其应用于更换图像背景。

首先，通过分析背景区域的 RGB 直方图，确定绿色背景的取值范围，从而生成了一个掩码。然而，发现 RGB 空间中的分割效果不佳，因此转向 YCbCr 空间进行颜色分割，即分析 Cb 和 Cr 分量的直方图。然后，使用阈值分割成功地提取了绿色背景。随后进行背景替换，最后实现对亮点的检测和提取。

图像的几何变换

目标： 理解并实现图像的几何变换，包括插值、坐标变换和单应变换。

使用最近邻、双线性和双三次插值方法，对提取的图像部分进行了插值放大。比较后，发现双三次插值方法的效果最佳，边缘更平滑。接下来，使用极坐标变换和插值来展开全景图像。使用矩阵 H 来实现图像的平移、缩放和旋转。最后进行单应变换，类似于将一张纸从一个摄像机视角转换到另一个视角，实质上是图像平面的变换。

第一部分 图像合成

目标： 合成一幅包含红、绿、蓝三个圆及其重叠部分的图像，以实现颜色的叠加。

已知数据：

• 图像大小： 256 \times 256

• 圆的半径：r = 70

• 图像中心到三个圆心的距离：d = 45

• 通过红色和绿色圆盘的线与水平轴之间的角度： \pi/6

RGB 颜色合成

a） 定义变量 r 和 d，计算三个圆心的坐标 x_0, y_0（以图像中心 (128,128) 为参考）。

#%% 问题 1a
image_center_x = 128
image_center_y = 128
r = 70   # 圆的半径
d = 45   # 图像中心到圆心的距离

# 角度
theta_R = m.pi / 6         # 红色圆的角度，30°
theta_G = 5 * m.pi / 6     # 绿色圆的角度，150°
theta_B = 3 * m.pi / 2     # 蓝色圆的角度，270°

# 计算圆心坐标
# 红色圆
X0_R = image_center_x + d * m.cos(theta_R)
Y0_R = image_center_y - d * m.sin(theta_R)

# 绿色圆
X0_G = image_center_x + d * m.cos(theta_G)
Y0_G = image_center_y - d * m.sin(theta_G)

# 蓝色圆
X0_B = image_center_x + d * m.cos(theta_B)
Y0_B = image_center_y - d * m.sin(theta_B)

print(f"红色圆的圆心: ({X0_R}, {Y0_R})")
print(f"绿色圆的圆心: ({X0_G}, {Y0_G})")
print(f"蓝色圆的圆心: ({X0_B}, {Y0_B})")

得到以下结果：

• 红色圆的圆心: (166.97114317029974, 105.5)

• 绿色圆的圆心: (89.02885682970026, 105.5)

• 蓝色圆的圆心: (127.99999999999999, 173.0)

b） 计算所选圆的掩码，即一个 256 \times 256 的标量图像 V，其中圆内的像素值为 1，其他位置为 0。可以定义一个中间矩阵 D 表示到圆心的距离。

使用显式循环：

#%% 问题 1b
M, N = 256, 256
# 计算每个像素到红色圆心的距离
D_R = np.zeros((M, N))
for i in range(M):
    for j in range(N):
        D_R[i, j] = np.sqrt((j - X0_R) ** 2 + (i - Y0_R) ** 2)
V_R = np.where(D_R <= r, 1, 0).astype(np.uint8)

# 计算每个像素到绿色圆心的距离
D_G = np.zeros((M, N))
for i in range(M):
    for j in range(N):
        D_G[i, j] = np.sqrt((j - X0_G) ** 2 + (i - Y0_G) ** 2)
V_G = np.where(D_G <= r, 1, 0).astype(np.uint8)

# 计算每个像素到蓝色圆心的距离
D_B = np.zeros((M, N))
for i in range(M):
    for j in range(N):
        D_B[i, j] = np.sqrt((j - X0_B) ** 2 + (i - Y0_B) ** 2)
V_B = np.where(D_B <= r, 1, 0).astype(np.uint8)

# 组合三个通道形成彩色图像
R = V_R * 255
G = V_G * 255
B = V_B * 255
img_RGB = np.stack((R, G, B), axis=2)

# 显示结果
cv2.imshow("RGB Disk Mask", img_RGB)
cv2.waitKey(0)
cv2.destroyAllWindows()

c） 使用隐式循环实现相同的计算：

#%% 问题 1c
# 使用隐式循环计算掩码
M, N = 256, 256

# 创建坐标网格
D_x, D_y = np.meshgrid(range(M), range(N))

# 到红色圆心的距离矩阵
D_R = np.sqrt((D_x - X0_R) ** 2 + (D_y - Y0_R) ** 2)
V_R = np.where(D_R <= r, 1, 0).astype(np.uint8)

# 到绿色圆心的距离矩阵
D_G = np.sqrt((D_x - X0_G) ** 2 + (D_y - Y0_G) ** 2)
V_G = np.where(D_G <= r, 1, 0).astype(np.uint8)

# 到蓝色圆心的距离矩阵
D_B = np.sqrt((D_x - X0_B) ** 2 + (D_y - Y0_B) ** 2)
V_B = np.where(D_B <= r, 1, 0).astype(np.uint8)

d） 为每个圆生成掩码，并推导出对应于每个颜色通道 R、G 和 B 的矩阵，其值范围为 0 到 255。

# 组合三个通道形成彩色图像
R = V_R * 255
G = V_G * 255
B = V_B * 255

e） 沿第三维将三个通道 R、G 和 B 组合成一个 256 \times 256 \times 3 的矩阵。

img_RGB = np.stack((B, G, R), axis=2)

cv2.imshow("RGB Disk Mask", img_RGB)
cv2.waitKey(0)
# cv2.destroyAllWindows()

图像 1：RGB 圆形掩码

​

索引颜色的合成

a） 使用 PIL 库定义一个包含 8 种颜色的调色板，用于索引颜色的合成。调色板的颜色顺序为：黑、红、绿、黄、蓝、品红、青和白。

#%% 问题 2a
from PIL import Image
# 定义包含 8 种颜色的调色板
palette = [   0, 0, 0,    # 黑
            255, 0, 0,    # 红
            0, 255, 0,    # 绿
            255, 255, 0,  # 黄
            0, 0, 255,    # 蓝
            255, 0, 255,  # 品红
            0, 255, 255,  # 青
            255, 255, 255]  # 白

# 创建一个 PIL 图像并应用调色板
img_indexed = Image.new("P", (M, N))  
img_indexed.putpalette(palette)

b） 使用显式循环遍历每个像素位置，并为每个像素赋予对应的颜色索引。例如，对于位置 (i,j) 的像素：

#%% 问题 2b
# 初始化图像大小
M, N = 256, 256
# 初始化索引图像矩阵
indexed_img = np.zeros((M, N), dtype=np.uint8)

# 使用显式循环分配颜色索引
for i in range(M):
    for j in range(N):
        if R[i, j] == 0 and G[i, j] == 0 and B[i, j] == 0:
            indexed_img[i, j] = 0  # 黑色
        elif R[i, j] == 255 and G[i, j] == 0 and B[i, j] == 0:
            indexed_img[i, j] = 1  # 红色
        elif R[i, j] == 0 and G[i, j] == 255 and B[i, j] == 0:
            indexed_img[i, j] = 2  # 绿色
        elif R[i, j] == 255 and G[i, j] == 255 and B[i, j] == 0:
            indexed_img[i, j] = 3  # 黄色
        elif R[i, j] == 0 and G[i, j] == 0 and B[i, j] == 255:
            indexed_img[i, j] = 4  # 蓝色
        elif R[i, j] == 255 and G[i, j] == 0 and B[i, j] == 255:
            indexed_img[i, j] = 5  # 品红
        elif R[i, j] == 0 and G[i, j] == 255 and B[i, j] == 255:
            indexed_img[i, j] = 6  # 青色
        elif R[i, j] == 255 and G[i, j] == 255 and B[i, j] == 255:
            indexed_img[i, j] = 7  # 白色

# 将生成的索引矩阵转换为 PIL 图像
img_indexed = Image.fromarray(indexed_img, mode='P')
img_indexed.putpalette(palette)
img_indexed.show()

c） 不使用显式循环实现相同的操作。颜色索引可以根据掩码的二进制编码进行排序，索引的计算如下：

#%% 问题 2c
# 定义图像大小
M, N = 256, 256
# 使用矢量化操作直接计算颜色索引
indexed_img = 1 * (R > 0) + 2 * (G > 0) + 4 * (B > 0)

# 定义包含 8 种颜色的调色板
palette = [ 0, 0, 0,      # 黑色
            255, 0, 0,    # 红色
            0, 255, 0,    # 绿色
            255, 255, 0,  # 黄色
            0, 0, 255,    # 蓝色
            255, 0, 255,  # 品红
            0, 255, 255,  # 青色
            255, 255, 255]# 白色

# 将生成的索引矩阵转换为 PIL 图像
img_indexed = Image.fromarray(indexed_img.astype(np.uint8), mode='P')
img_indexed.putpalette(palette)
img_indexed.show()

图像 2：索引颜色的 RGB 圆形掩码

​

颜色索引是一种有效减少存储空间的方法。我们不需要为每个像素存储完整的 RGB 值，只需存储指向调色板中预定义颜色的索引。

第二部分 线性滤波

低通滤波/平滑

目标： 我们在此考虑一个 3 \times 3 的均值滤波器：

使用此滤波器，我们将观察或消除特定的频谱分量，最终观察其效果。

1. 低通滤波的空间效应

a） 加载图像 batiment.bmp

# 问题 1a
image = cv2.imread('batiment.bmp')

b） 定义要应用的滤波器 h

# 问题 1b
h = np.ones((3, 3), np.float32) / 9

c） 将滤波器 h 应用于图像，并显示滤波前后的图像

# 问题 1c
filtered_image = cv2.filter2D(image, -1, h)

# 显示滤波前后的图像
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title("原始图像")
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.axis('off')
plt.subplot(1, 2, 2)
plt.title("滤波后的图像")
plt.imshow(cv2.cvtColor(filtered_image, cv2.COLOR_BGR2RGB))
plt.axis('off')
plt.show()

d） 评论低通滤波的空间效应

图像 3：原始图像与滤波后的图像比较

​

均值滤波器通过将每个像素的值与其邻域像素的值进行平均，可以消除高频噪声，如边缘或纹理细节，从而使图像更加模糊或平滑。但这也会导致细节的丢失。

2. 在频率域的效果

a） 显示滤波前后图像的傅里叶变换的模：

#%% 问题 2a
# 计算傅里叶变换的绝对值并显示
FT_I = np.log10(np.abs(np.fft.fftshift(np.fft.fft2(image[:, :, 0]))))
FT_filterI = np.log10(np.abs(np.fft.fftshift(np.fft.fft2(filtered_image[:, :, 0]))))

plt.figure(figsize=(10, 5))

plt.subplot(1, 2, 1)
plt.title("原始图像的傅里叶变换")
plt.imshow(FT_I, cmap='gray')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.title("滤波后图像的傅里叶变换")
plt.imshow(FT_filterI, cmap='gray')
plt.axis('off')

plt.show()

图像 4：滤波前后傅里叶变换的比较

​

b） 使用以下定义的函数 freqz_2 显示滤波器的频率响应：

#%% 问题 2b
def freqz_2(X, row, col):
    s = X.shape
    zeros_padd = np.zeros((row, col))
    zeros_padd[int((row - s[0]) / 2):int(((row - s[0]) / 2) + s[0]), 
               int((col - s[1]) / 2):int(((col - s[1]) / 2) + s[1])] = X
    freqz2_X = np.abs(np.fft.fftshift(np.fft.fft2(zeros_padd)))
    return freqz2_X

filter_freq_response = freqz_2(h, image.shape[0], image.shape[1])

# 显示滤波器的频率响应
plt.figure()
plt.imshow(np.log10(filter_freq_response), cmap='gray')
plt.title("3x3 均值滤波器的频率响应")
plt.colorbar()
plt.show()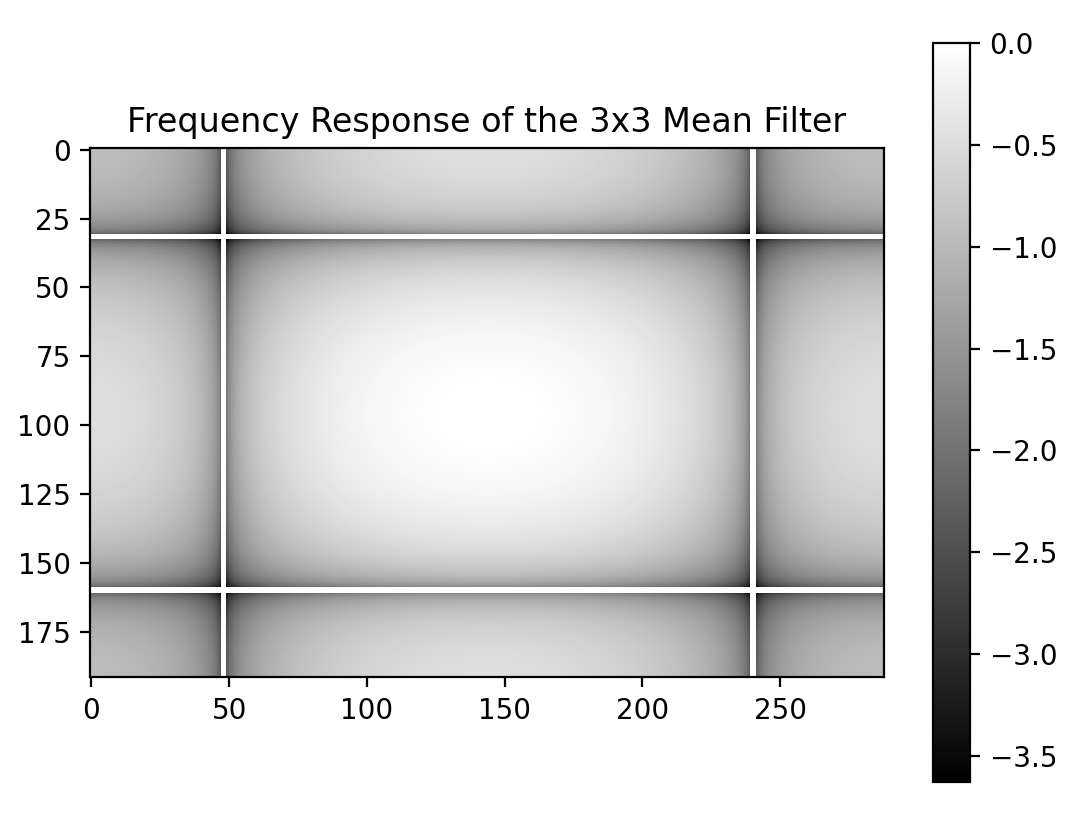

图像 5：均值滤波器的频率响应

​

c） 将滤波前后图像的傅里叶变换与滤波器的频率响应联系起来

在均值滤波器的频率响应中，低频部分更亮，而高频部分更暗。这表明在低通滤波后，图像的高频分量被衰减。在滤波后的图像频率域中，位于中心的低频占主导地位，而高频部分被减弱。

3. 应用于图像去噪

本部分的目标是首先在频率域中识别图像（monument.bmp）上可见的噪声模式，然后生成一个适合衰减它们的有限冲激响应（FIR）线性滤波器。

a） 加载带有高频加性噪声的图像 monument.bmp。显示噪声图像及其傅里叶变换，定位噪声的频率。

#%% 问题 3a
image_noisy = cv2.imread('monument.bmp', cv2.IMREAD_GRAYSCALE)

# 计算傅里叶变换的绝对值并显示
FT_noisy = np.log10(np.abs(np.fft.fftshift(np.fft.fft2(image_noisy))))

# 显示噪声图像及其傅里叶变换
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title("带噪声的图像")
plt.imshow(image_noisy, cmap='gray')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.title("噪声图像的傅里叶变换")
plt.imshow(FT_noisy, cmap='gray')
plt.colorbar()
plt.axis('off')
plt.show()

图像 6：带噪声的图像及其傅里叶变换

​

b） 使用低通滤波器对图像进行去噪。

• 可以使用的滤波器类型包括：均值滤波器（average）、圆盘滤波器（disk）、高斯滤波器（gaussian）。

• 对于每个滤波器，显示去噪后的图像、其傅里叶变换，以及去噪图像与噪声图像之间的差异。判断滤波是否有效。

#%% 问题 3b
# 使用不同类型的滤波器进行去噪
# 使用均值滤波器
average_filtered = cv2.blur(image_noisy, (5, 5))
# 使用圆盘滤波器（使用 OpenCV 的中值滤波作为近似）
disk_filtered = cv2.medianBlur(image_noisy, 5)
# 使用高斯滤波器
gaussian_filtered = cv2.GaussianBlur(image_noisy, (5, 5), 0)

# 显示滤波后的图像及其傅里叶变换
def plot_filtered_image_and_fft(filtered_image, filter_name):
    # 计算傅里叶变换的绝对值
    FT_filtered = np.log10(np.abs(np.fft.fftshift(np.fft.fft2(filtered_image))) + 1)
    
    plt.figure(figsize=(15, 5))
    plt.subplot(1, 3, 1)
    plt.title(f"{filter_name} 滤波后的图像")
    plt.imshow(filtered_image, cmap='gray')
    plt.axis('off')
    
    plt.subplot(1, 3, 2)
    plt.title(f"{filter_name} 滤波后图像的傅里叶变换")
    plt.imshow(FT_filtered, cmap='gray')
    plt.colorbar()
    plt.axis('off')
    
    plt.subplot(1, 3, 3)
    plt.title(f"差异（噪声 - {filter_name}）")
    difference = image_noisy - filtered_image
    plt.imshow(difference, cmap='gray')
    plt.colorbar()
    plt.axis('off')
    plt.tight_layout()
    plt.show()

# 显示均值滤波的去噪效果
plot_filtered_image_and_fft(average_filtered, '均值')

# 显示圆盘滤波的去噪效果
plot_filtered_image_and_fft(disk_filtered, '圆盘')

# 显示高斯滤波的去噪效果
plot_filtered_image_and_fft(gaussian_filtered, '高斯')

​

图像 7：均值滤波去噪结果

​

​

图像 8：圆盘滤波去噪结果

​

​

图像 9：高斯滤波去噪结果

​

理论上，高斯滤波器应优于均值滤波器，因为它对中心像素赋予更高的权重，逐渐减小对远处像素的影响。然而，在实际图像中，差异图像的分析表明，高斯滤波器相较于均值滤波器并没有带来显著的改进，而圆盘滤波器的去噪效果更为有效。

c） 我们现在设计一个高斯型“带阻”滤波器（消除特定频带的信息）。此滤波器将在空间域中构建并应用（对图像进行卷积），但其傅里叶变换将表现为带阻滤波器（在噪声频率的位置产生两个“凹陷”）。

为了在频率域中创建此带阻滤波器，我们将分三步进行：

1. 首先创建一个低通滤波器，定义为以零为中心的二维高斯函数：

   g_{\text{pbas}}(x, y) = \frac{1}{2\pi\sigma^2} \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)

   
   

   在频率域中，高斯函数的方差为 \sigma，其傅里叶变换也是一个方差为 1/\sigma 的高斯函数。

2. 然后，通过一个正弦信号对其进行调制，使其中心位于噪声的频率上，从而创建一个带通滤波器：

   g_{\text{pbande}}(x, y) = g_{\text{pbas}} \cdot 2 \cdot \cos\left(2\pi(f_x x + f_y y)\right)

   
   

   在空间域中乘以一个余弦函数，相当于在频率域中将 g_{\text{pbas}} 的傅里叶变换与余弦函数的傅里叶变换（即在噪声频率处的两个狄拉克函数）进行卷积。

3. 最后，将此滤波器转换为频率域中的带阻滤波器：

   g_{\text{cbande}} = \delta - g_{\text{pbande}}

   
   

   对于中心为零的狄拉克函数（矩阵中心值为 1，其他元素为 0），其傅里叶变换在频率域中处处为 1。因此，带阻滤波器的频率响应为：

   G_{\text{cbande}} = 1 - G_{\text{pbande}}

要求完成的任务：

• 在每个步骤中构建滤波器，并在空间域和频率域中可视化其效果。

• 评论将最终滤波器应用于带噪声图像的效果，特别是不同参数的影响。

#%% 问题 3c
image_path = 'monument.bmp'
image_noisy = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
if image_noisy is None:
    raise ValueError("图像无法读取，请检查文件路径")

rows, cols = image_noisy.shape
x_center, y_center = cols // 2, rows // 2

sigma = 100
fx, fy = 30, 30

# 构建空间域坐标, 以图像中心为原点
x = np.arange(cols) - x_center
y = np.arange(rows) - y_center
X, Y = np.meshgrid(x, y)

# 1) 构建高斯低通滤波器 g_pbas(x,y)
g_pbas = (1/(2*np.pi*sigma**2)) * np.exp(-(X**2 + Y**2)/(2*sigma**2))

# 2) 构建带通滤波器 g_pbande(x,y)
g_pbande = g_pbas * 2 * np.cos(2*np.pi*(fx*X/cols + fy*Y/rows))

# 3) 构建带阻滤波器 g_cbande(x,y)
delta = np.zeros_like(g_pbande)
# 在中心点处为1，即 δ(y_center, x_center)=1
delta[y_center, x_center] = 1
g_cbande = delta - g_pbande

# ---- 关键修改部分开始 ----
# 将滤波器从中心对齐转换为左上角对齐，以便后续的 FFT 与卷积正确对应
g_cbande_for_fft = np.fft.ifftshift(g_cbande)
# ---- 关键修改部分结束 ----

# 计算滤波器频域特性
F_g_cbande = np.fft.fft2(g_cbande_for_fft)

# 对带噪声图像进行FFT（无需 shift）
FT_noisy = np.fft.fft2(image_noisy)

# 在频域中进行滤波
FT_filtered = FT_noisy * F_g_cbande

# 逆变换回空间域
filtered_image = np.fft.ifft2(FT_filtered)
filtered_image = np.abs(filtered_image)

# 显示结果
plt.figure(figsize=(12,6))
plt.subplot(1, 2, 1)
plt.title("Filtered Image (Band-Stop)")
plt.imshow(filtered_image, cmap='gray')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.title("Fourier Transform of Filtered Image")
plt.imshow(np.log10(np.abs(FT_filtered)+1), cmap='gray')
plt.colorbar()
plt.axis('off')

plt.tight_layout()
plt.show()

注：由于噪声频率需要根据傅里叶变换图像手动调整，因此 fx 和 fy 的值可能需要根据实际情况修改。

• 关于 \sigma 的选择：

  标准差 \sigma 决定了高斯滤波器的宽度，σ 的选择需兼顾噪声频带与原图像频谱成分的分布：

  • 若 σ 太小，高斯低通会很窄，带通或带阻对频率敏感度高，但无法完全覆盖噪声带宽。

  • 若 σ 太大，高斯低通会变得过宽，带阻滤波不够精准，破坏原有图像细节。

  • 要确保不违反 Shannon 采样定理（即不去滤除在有效可表示频带内的有效成分）

• 滤波效果：

  通过在空间域中构建带阻滤波器，可以在频率域中有效地抑制特定频率的噪声，从而改善图像的质量。

高通滤波与对比度增强

目标： 在图像上应用卷积型高通滤波器，并观察其效果

1. 拉普拉斯滤波器

拉普拉斯算子的二维卷积掩码可表示为：

a） 将此滤波器应用于图像并观察其空间效果。

#%% 问题 1a
# 定义拉普拉斯滤波器
laplacian_filter = np.array([[0, 1, 0],
                             [1, -4, 1],
                             [0, 1, 0]])
# 应用卷积操作
filtered_image = cv2.filter2D(image_noisy, -1, laplacian_filter)

# 显示原始图像和滤波后的图像
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title("原始图像")
plt.imshow(image_noisy, cmap='gray')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.title("拉普拉斯滤波后的图像")
plt.imshow(filtered_image, cmap='gray')
plt.axis('off')
plt.tight_layout()
plt.show()

​

图像 10：拉普拉斯滤波效果

​

b） 显示输入和输出图像的傅里叶变换。

# 问题 1b
# 计算傅里叶变换的绝对值并显示
FT_original = np.log10(np.abs(np.fft.fftshift(np.fft.fft2(image_noisy))) + 1)
FT_filtered = np.log10(np.abs(np.fft.fftshift(np.fft.fft2(filtered_image))) + 1)

plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title("原始图像的傅里叶变换")
plt.imshow(FT_original, cmap='gray')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.title("滤波后图像的傅里叶变换")
plt.imshow(FT_filtered, cmap='gray')
plt.axis('off')
plt.show()

​

图像 11：拉普拉斯滤波前后的傅里叶变换

​

从数学公式的角度来看，中心系数为 -4，这意味着对中心像素应用了一个负权重，而对周围像素应用了正权重。因此，它可以检测图像中像素值的变化，即边缘的位置。

从结果来看，拉普拉斯滤波器主要关注图像的边缘（像素快速变化的地方）。应用拉普拉斯滤波器后，图像的边缘被显著增强（非常清晰），而平滑区域变得更暗。

我们可以使用拉普拉斯滤波器来提取图像的边缘。

2. 应用于对比度增强

a） 将掩码 L 应用于图像 moon.tif，然后根据以下公式从原始图像中减去结果：

其中 \alpha 是一个调整参数，可以任意设置为正值，例如 1。

观察不同 \alpha 值（例如 0、1、2、-0.25）下的结果。

#%% 问题 2a
# 加载图像
image_moon = cv2.imread('moon.tif', cv2.IMREAD_GRAYSCALE)

# 应用拉普拉斯滤波器
laplacian_result = cv2.filter2D(image_moon, -1, laplacian_filter)

# 对比度增强
alpha_values = [0, 1, 2, -0.25]
plt.figure(figsize=(15, 6))
for i, alpha in enumerate(alpha_values):
    image_moon_enhance = cv2.addWeighted(image_moon, 1, laplacian_result, -alpha, 0)
    
    plt.subplot(1, len(alpha_values), i + 1)
    plt.title(f'alpha = {alpha}')
    plt.imshow(image_moon_enhance, cmap='gray')
    plt.axis('off')

plt.tight_layout()
plt.show()

​

图像 12：不同 α 值下的对比度增强

​

b） 从空间域和频率域的角度解释为什么能增强图像的边缘。

• 从空间域的角度：

  拉普拉斯算子是一个二阶微分算子，能够检测图像中变化迅速的区域（即边缘）。

  公式 K(x, y) = I(x, y) - \alpha J(x, y) 是对比度增强的关键公式。通过选择不同的调整参数 \alpha，可以获得对边缘的不同效果。

  • 当 \alpha > 0 时，边缘被增强，图像的对比度提高。

  • 当 \alpha < 0 时，边缘被削弱，图像变得模糊或平滑。

  • 当 \alpha = 0 时，图像不发生变化。

• 从频率域的角度：

  拉普拉斯滤波器相当于一个高通滤波器，因为它增强了高频分量，从而改善了图像的边缘。

第三部分 颜色分割

目标： 对彩色图像进行 RGB 或 YCbCr 分割，并更换图像的背景。

在 RGB 空间中的分割

a） 加载图像 homme_green.png。分别显示图像的 3 个 RGB 通道。

#%% 练习 3 - 问题 1a
image = cv2.imread('homme_green.png')
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
R, G, B = image_rgb[:, :, 0], image_rgb[:, :, 1], image_rgb[:, :, 2]

# 显示 RGB 通道
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.title('红色通道')
plt.imshow(R, cmap='gray')
plt.axis('off')
plt.subplot(1, 3, 2)
plt.title('绿色通道')
plt.imshow(G, cmap='gray')
plt.axis('off')
plt.subplot(1, 3, 3)
plt.title('蓝色通道')
plt.imshow(B, cmap='gray')
plt.axis('off')
plt.tight_layout()
plt.show()

​

图 13：RGB 通道的分离

​

b） 对于每个通道，确定一个包含所有绿色背景像素的区间 ( [R{\text{min}}, R{\text{max}}] )。通过计算仅包含背景部分的图像的每个颜色分量的直方图，验证所选的区间。

#%% 问题 1b
# 显示每个通道的直方图
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.title('红色通道直方图')
plt.hist(R.ravel(), bins=256, color='red')
plt.xlabel('像素值')
plt.ylabel('频率')
plt.subplot(1, 3, 2)
plt.title('绿色通道直方图')
plt.hist(G.ravel(), bins=256, color='green')
plt.xlabel('像素值')
plt.ylabel('频率')
plt.subplot(1, 3, 3)
plt.title('蓝色通道直方图')
plt.hist(B.ravel(), bins=256, color='blue')
plt.xlabel('像素值')
plt.tight_layout()
plt.show()

# 创建一个掩码来分离背景
mask = (R >= 0) & (R <= 50) & (G >= 220) & (G <= 256) & (B >= 0) & (B <= 50)
R_segmented = image[:, :, 0] * mask
G_segmented = image[:, :, 1] * mask
B_segmented = image[:, :, 2] * mask

image_segmented = cv2.merge((B_segmented, G_segmented, R_segmented))

# 显示分割后的图像
plt.figure()
plt.title('RGB 空间中的分割图像')
plt.imshow(image_segmented)
plt.axis('off')
plt.show()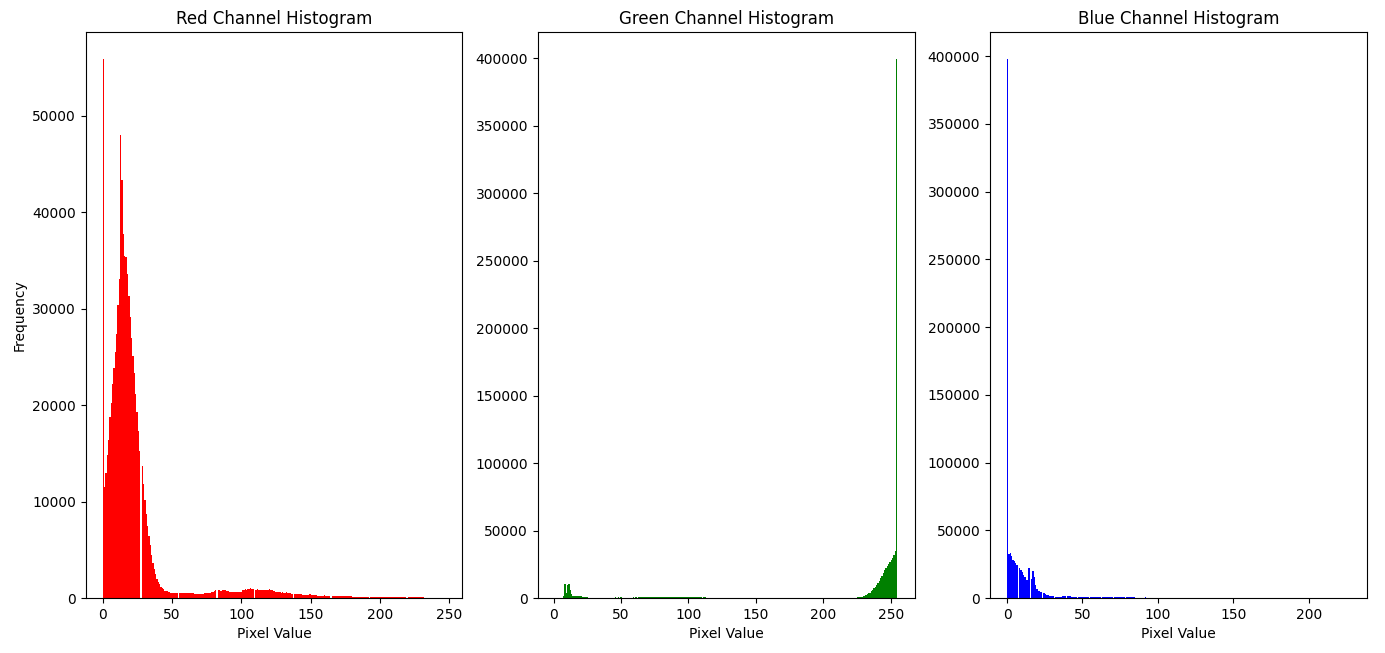

​

图像 14：RGB 通道的直方图

​

​

图像 15：RGB 空间中的分割结果

​

通过观察 RGB 通道的直方图，可以有效地确定绿色背景像素的范围，并使用这些范围进行颜色分割。选择的阈值确保了大多数绿色背景的像素被正确识别，同时将对前景人物的影响最小化。但是，背景中仍有一些黑点。通过调整适当的阈值，能够获得更好的结果。

在 YCbCr 空间中的分割

a） 将 RGB 图像转换为 YCbCr 图像，并显示其不同的分量。

#%% 问题 2a

# 将 RGB 图像转换为 YCbCr
image_ycbcr = cv2.cvtColor(image_rgb, cv2.COLOR_RGB2YCrCb)
# 分离 Y、Cb、Cr 通道
Y, Cb, Cr = image_ycbcr[:, :, 0], image_ycbcr[:, :, 1], image_ycbcr[:, :, 2]

# 创建一个 2 行 3 列的子图布局
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
# 显示 Y、Cb、Cr 通道
axes[0, 0].set_title('Y 通道')
axes[0, 0].imshow(Y, cmap='gray')
axes[0, 0].axis('off')
axes[0, 1].set_title('Cb 通道')
axes[0, 1].imshow(Cb, cmap='gray')
axes[0, 1].axis('off')
axes[0, 2].set_title('Cr 通道')
axes[0, 2].imshow(Cr, cmap='gray')
axes[0, 2].axis('off')

# 显示每个通道的直方图
axes[1, 0].set_title('Y 通道直方图')
axes[1, 0].hist(Y.ravel(), bins=256, color='blue')
axes[1, 0].set_xlabel('像素值')
axes[1, 0].set_ylabel('频率')
axes[1, 1].set_title('Cb 通道直方图')
axes[1, 1].hist(Cb.ravel(), bins=256, color='red')
axes[1, 1].set_xlabel('像素值')
axes[1, 1].set_ylabel('频率')
axes[1, 2].set_title('Cr 通道直方图')
axes[1, 2].hist(Cr.ravel(), bins=256, color='green')
axes[1, 2].set_xlabel('像素值')
axes[1, 2].set_ylabel('频率')

plt.tight_layout()
plt.show()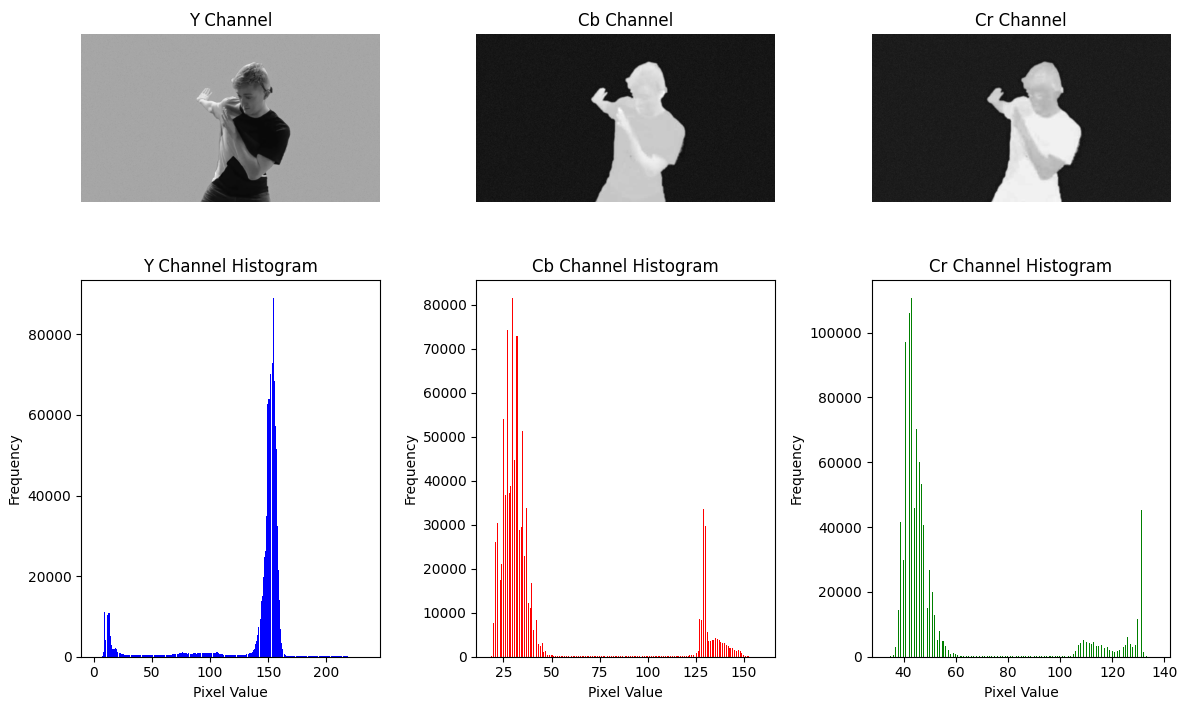

​

图像 16：YCbCr 通道及其直方图

​

b） 对背景进行分割

#%% 问题 2b
# 使用 YCbCr 空间进行背景分割
mask = ((Cb >= 15) & (Cb <= 50)) & ((Cr >= 35) & (Cr <= 60))

Y_segmented = Y * mask
Cb_segmented = Cb * mask
Cr_segmented = Cr * mask

image_background = cv2.merge((Y_segmented, Cb_segmented, Cr_segmented))

# 显示分割后的背景图像
plt.figure()
plt.title('YCbCr 空间中的分割图像')
plt.imshow(image_background)
plt.axis('off')
plt.show()

​

图像 17：YCbCr 空间中的分割结果

​

与 RGB 空间相比，YCbCr 空间将亮度信息（Y）与色度信息（Cb、Cr）分离，这使得颜色分割更加精确。在复杂的光照条件下，YCbCr 空间中的分割可以减少光照对颜色分布的影响，从而改善分割效果。

色度键合成

a） 使用之前计算的掩码作为权重，将分割的背景替换为另一幅背景图像（montagne.png）。

#%% 问题 3a

# 读取原始图像和新的背景图像
image = cv2.imread('homme_green.png')
new_background = cv2.imread('montagne.png')

# 确保尺寸一致
new_background = cv2.resize(new_background, (image.shape[1], image.shape[0]))

# 将新的背景图像转换为 YCbCr
new_background_ycbcr = cv2.cvtColor(new_background, cv2.COLOR_BGR2YCrCb)
Y_bg, Cb_bg, Cr_bg = new_background_ycbcr[:, :, 0], new_background_ycbcr[:, :, 1], new_background_ycbcr[:, :, 2]

# 反转掩码以分离前景
mask_inv = 1 - mask

# 分离前景
Y_segmented = Y * mask_inv
Cb_segmented = Cb * mask_inv
Cr_segmented = Cr * mask_inv

image_foreground = cv2.merge((Y_segmented, Cb_segmented, Cr_segmented))

# 分离背景
Y_background = Y_bg * mask
Cb_background = Cb_bg * mask
Cr_background = Cr_bg * mask

background = cv2.merge((Y_background, Cb_background, Cr_background))

# 合并前景和背景
final_image_ycbcr = image_foreground + background

# 转换回 BGR 色彩空间
final_image_ycbcr = final_image_ycbcr.astype('uint8')
final_result = cv2.cvtColor(final_image_ycbcr, cv2.COLOR_YCrCb2BGR)

# 显示色度键合成后的图像
plt.figure(figsize=(8, 6))
plt.title('色度键合成结果')
plt.imshow(cv2.cvtColor(final_result, cv2.COLOR_BGR2RGB))
plt.axis('off')
plt.show()

​

图像 18：替换背景后的图像

​

我们成功地将绿色背景替换为新的背景图像。色度键合成技术利用了色彩空间中分离的色度信息，确保前景人物的颜色不受新背景的影响，从而实现了背景替换的效果。

斑点检测

a） 对图像 mocap.jpg 的亮度进行阈值处理，分割饱和的白色斑点：

#%% 问题 4a
# 读取动作捕捉图像
image_mocap = cv2.imread('mocap.jpg')

# 转换为 YCbCr 色彩空间
image_ycbcr_mocap = cv2.cvtColor(image_mocap, cv2.COLOR_BGR2YCrCb)
Y_channel_mocap = image_ycbcr_mocap[:, :, 0]

# 通过阈值分割来检测饱和的白色斑点
_, M = cv2.threshold(Y_channel_mocap, 250, 255, cv2.THRESH_BINARY)

plt.figure()
plt.title('二值掩码（Y > 250）')
plt.imshow(M, cmap='gray')
plt.axis('off')
plt.show()

​

图像 19：亮点的二值掩码

​

我们得到了一幅二值图像，其中亮度大于 250 的像素被标记为 255（白色），其他像素为 0（黑色），从而有效地分割了饱和的白色斑点。

b） 使用 connectedComponents 函数对获得的二值图像进行连通区域的标记。然后，使用调色板显示标记的图像，突出显示不同连通区域的编号，即为每个连通区域分配不同的颜色。

#%% 问题 4b
# 连通区域标记
num_labels, labels_im = cv2.connectedComponents(M.astype(np.uint8), connectivity=8)

# 确认标签图像的大小
print("图像大小:", image_mocap.shape[:2])
print("标签图像大小:", labels_im.shape)

# 创建彩色标签图像
label_hue = np.uint8(179 * labels_im / np.max(labels_im))
blank_ch = 255 * np.ones_like(label_hue)
labeled_img = cv2.merge([label_hue, blank_ch, blank_ch])
labeled_img = cv2.cvtColor(labeled_img, cv2.COLOR_HSV2RGB)
labeled_img[label_hue == 0] = 0  # 将背景设为黑色

# 显示标记的图像
plt.figure()
plt.title("连通区域标记的图像")
plt.imshow(labeled_img)
plt.axis('off')
plt.show()

​

图像 20：连通区域标记的结果

​

c） 将检测到的斑点叠加在原始图像上。

#%% 问题 4c
# 创建叠加图像
overlay = image_mocap.copy()

# 为每个连通区域（除背景标签 0 外）分配随机颜色
colors = []
for i in range(1, num_labels):
    colors.append(np.random.randint(0, 255, 3))

# 将颜色应用于每个连通区域
for label in range(1, num_labels):
    overlay[labels_im == label] = colors[label - 1]

# 将标签图像叠加在原始图像上
alpha = 0.5  # 透明度
result = cv2.addWeighted(image_mocap, 1 - alpha, overlay, alpha, 0)

# 显示叠加后的图像
plt.figure()
plt.title("检测到的斑点叠加在原始图像上")
plt.imshow(cv2.cvtColor(result, cv2.COLOR_BGR2RGB))
plt.axis('off')
plt.show()

​

图像 21：检测到的亮点叠加在原始图像上

​通过应用阈值分割和连通区域标记，我们将标记的图像叠加在原始图像上，调整透明度参数 \alpha 来控制权重。

第四部分 图像的几何变换

目标： 应用不同的插值方法对图像进行过采样，以观察它们对图像质量和频域特性的影响。

过采样 / 插值

a） 从图像 lena256.png 中提取眼睛区域（ymin:ymax=120:149, xmin:xmax=120:149），使用最近邻、双线性和双三次插值方法将其放大 5 倍。

#%% 问题 1a
# 加载图像
img = cv2.imread('lena256.png')

# 转换为 RGB 格式以便显示（OpenCV 默认使用 BGR）
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 提取眼睛区域
x_min, x_max = 120, 149
y_min, y_max = 120, 149
eye_region = img_rgb[y_min:y_max, x_min:x_max]

# 定义新尺寸（放大 5 倍）
scale_factor = 5
new_size = (eye_region.shape[1] * scale_factor, eye_region.shape[0] * scale_factor)

# 应用不同的插值方法
eye_nearest = cv2.resize(eye_region, new_size, interpolation=cv2.INTER_NEAREST)
eye_bilinear = cv2.resize(eye_region, new_size, interpolation=cv2.INTER_LINEAR)
eye_bicubic = cv2.resize(eye_region, new_size, interpolation=cv2.INTER_CUBIC)

# 显示原始和插值后的图像以进行比较
fig, axs = plt.subplots(1, 4, figsize=(16, 4))

axs[0].imshow(eye_region)
axs[0].set_title('原始图像')
axs[0].axis('off')

axs[1].imshow(eye_nearest)
axs[1].set_title('最近邻插值')
axs[1].axis('off')

axs[2].imshow(eye_bilinear)
axs[2].set_title('双线性插值')
axs[2].axis('off')

axs[3].imshow(eye_bicubic)
axs[3].set_title('双三次插值')
axs[3].axis('off')

plt.tight_layout()
plt.show()

​

图像 22：插值方法的比较

​

最近邻插值为每个新像素分配最接近的现有像素的值，这会导致锯齿状边缘和细节的丢失。双线性插值使用最接近的 4 个像素的加权平均值，这使过渡更平滑，减少了块效应。双三次插值使用 16 个相邻像素进行更精确的估计，保留更多细节，生成更平滑的图像。

b） 显示每个图像的水平轮廓线。

#%% 问题 1b
# 选择水平中心线
row = eye_region.shape[0] // 2

# 获取放大图像中该行的像素值
original_profile = eye_region[row, :, :]
nearest_profile = eye_nearest[row * scale_factor, :, :]
bilinear_profile = eye_bilinear[row * scale_factor, :, :]
bicubic_profile = eye_bicubic[row * scale_factor, :, :]

# 绘制颜色通道的值，并在一张图上显示所有方法
colors = ['红色通道', '绿色通道', '蓝色通道']

for i in range(3):
    plt.figure(figsize=(10, 6))
    plt.plot(original_profile[:, i], label='原始', linewidth=2)
    plt.plot(nearest_profile[:, i], label='最近邻', linestyle='--')
    plt.plot(bilinear_profile[:, i], label='双线性', linestyle='-.')
    plt.plot(bicubic_profile[:, i], label='双三次', linestyle=':')
    plt.title(f'{colors[i]} - 水平轮廓线比较')
    plt.legend()
    plt.xlabel('像素位置')
    plt.ylabel('像素值')
    plt.show()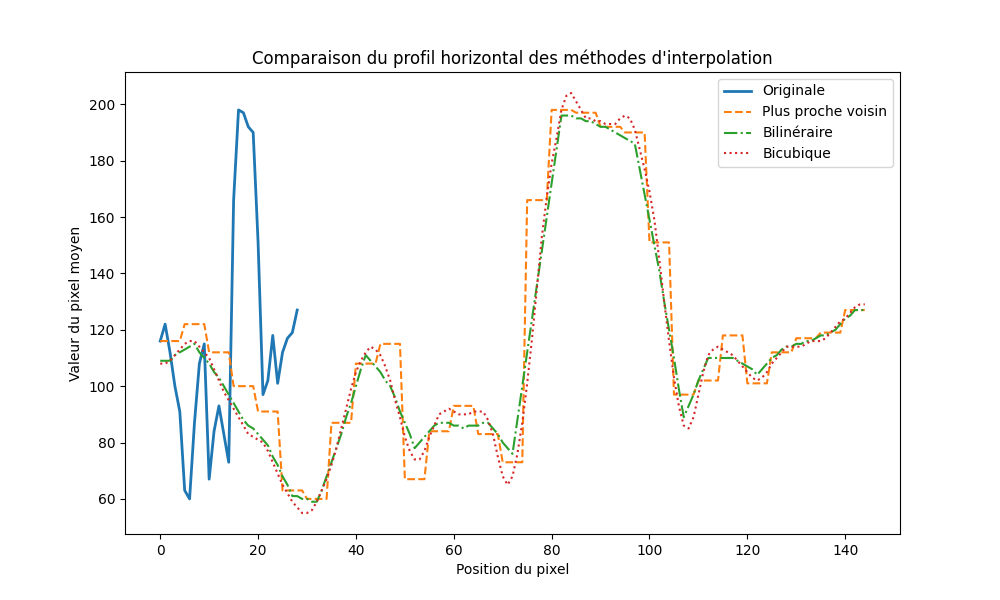

​

图 23：不同插值方法的水平轮廓线

​

c） 显示图像的傅里叶变换，并与初始图像进行比较。

#%% 问题 1c
def compute_fft(image):
    # 将图像转换为灰度
    gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
    # 计算傅里叶变换
    f = np.fft.fft2(gray)
    fshift = np.fft.fftshift(f)
    magnitude_spectrum = 20 * np.log(np.abs(fshift) + 1)  # 加 1 以避免 log(0)
    return magnitude_spectrum

# 计算傅里叶变换
fft_original = compute_fft(eye_region)
fft_nearest = compute_fft(eye_nearest)
fft_bilinear = compute_fft(eye_bilinear)
fft_bicubic = compute_fft(eye_bicubic)

# 显示傅里叶变换以进行比较
fig, axs = plt.subplots(2, 2, figsize=(12, 10))

axs[0, 0].imshow(fft_original, cmap='gray')
axs[0, 0].set_title('原始图像的傅里叶变换')
axs[0, 0].axis('off')

axs[0, 1].imshow(fft_nearest, cmap='gray')
axs[0, 1].set_title('最近邻插值的傅里叶变换')
axs[0, 1].axis('off')

axs[1, 0].imshow(fft_bilinear, cmap='gray')
axs[1, 0].set_title('双线性插值的傅里叶变换')
axs[1, 0].axis('off')

axs[1, 1].imshow(fft_bicubic, cmap='gray')
axs[1, 1].set_title('双三次插值的傅里叶变换')
axs[1, 1].axis('off')

plt.tight_layout()
plt.show()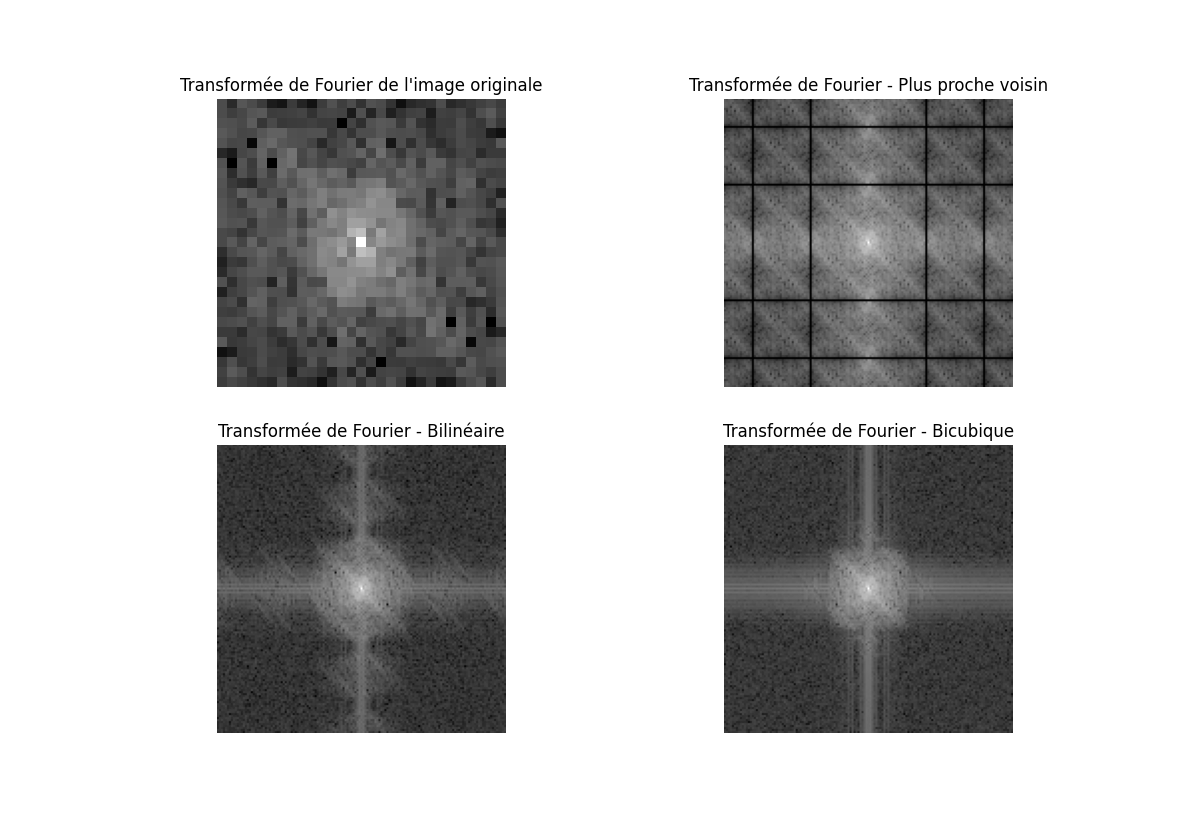

​

图 24：傅里叶变换的比较

​

最近邻插值由于在图像中产生的不连续性，会在频域中导致伪影和谐波的出现。双线性插值通过平滑过渡来减少这些效果，这在傅里叶变换中表现为高频分量的衰减。双三次插值在频域中最能保留原始图像的特征，频域中的失真较少。

图像变换

目标： 操作不同的几何变换模型，并将这些变换应用于图像。

笛卡尔 - 极坐标变换

我们希望将全向图像 omni.png 转换为全景图像，即将图像的内容转换为极坐标表示。

a） 加载包含全向图像的 omni.png，并将图像转换为灰度以简化处理。计算图像中心的坐标 x_0, y_0。

#%% 问题 2a
# 加载全向图像并转换为灰度
omni = cv2.imread('omni.png', cv2.IMREAD_GRAYSCALE)

# 获取图像的尺寸
height, width = omni.shape
x0, y0 = width // 2, height // 2

print(f"图像中心：({x0}, {y0})")

b） 使用 meshgrid 函数创建两个矩阵 X2 和 Y2，表示大小为 360×200 的目标图像的坐标。将 X2 解释为角度（在 0 到 360 度之间），Y2 解释为相对于中心 x_0, y_0 的半径。然后计算源图像中的对应坐标 (X1, Y1)。

#%% 问题 2b
# 定义目标图像的大小
theta_max, r_max = 360, 200
theta, r = np.meshgrid(np.linspace(0, 2 * np.pi, theta_max),
                       np.linspace(0, r_max, r_max))

# 计算源图像中的对应坐标
X1 = x0 + r * np.cos(theta)
Y1 = y0 + r * np.sin(theta)

c） 对先前计算的 (X1, Y1) 位置进行插值，并显示结果图像。绘制一个解释性示意图，说明此变换的原理，特别是解释直接/逆变换的概念。

#%% 问题 2c
from scipy.ndimage import map_coordinates

# 将坐标展平为 1D 向量
X1_flat = X1.flatten()
Y1_flat = Y1.flatten()

# 双线性插值
omni_polar = map_coordinates(omni, [Y1_flat, X1_flat], order=1, mode='constant', cval=0)

# 重塑为目标图像的大小
omni_polar = omni_polar.reshape((r_max, theta_max))

# 显示结果
plt.figure(figsize=(8, 6))
plt.imshow(omni_polar, cmap='gray', extent=(0, 360, 0, r_max))
plt.title('灰度全景图像（极坐标变换）')
plt.xlabel('角度（度）')
plt.ylabel('半径')
plt.axis('off')
plt.show()

​

图 25：全向图像的极坐标变换

极坐标变换是将源图像的笛卡尔坐标 (x, y) 重新映射为目标图像的极坐标 ( r, \theta )。逆变换用于确定目标图像中每个像素在源图像中的对应坐标。

笛卡尔坐标转换为极坐标：

极坐标转换为笛卡尔坐标：

直接变换是将图像从笛卡尔坐标系 M 转换到极坐标系 M'，步骤如下：

1. 确定极坐标下点 M' 在全景图像中的位置：

   假设我们有一幅原始图像，L 表示全景图像的宽度，a 表示原始图像的高度，b 表示原始图像的宽度。原始图像中的一个点表示为 M。

   对应的全景图像中的点 M' 具有极坐标 ( \theta, r )，定义为：

   \begin{cases} \theta = \frac{2 \pi L}{b} \\ r = \rho \cdot a \\ \rho = \frac{R}{2 \cdot a} \end{cases}

   其中 R 是全景图像的高度

2. 使用转换公式将极坐标转换为笛卡尔坐标：

   \begin{cases} x' = r \cdot \cos(\theta) \\ y' = r \cdot \sin(\theta) \end{cases}

3. 将原始图像中点 M 的灰度值赋给全景图像中的点 M'。

4. 应用插值以细化结果。

d） 对源图像的每个 R、G、B 分量 I(:, :, k) 应用相同的处理，以获得转换后的彩色图像。

#%% 问题 2d
# 加载彩色图像
omni_color = cv2.imread('omni.png')
# 转换为 RGB 格式
omni_color_rgb = cv2.cvtColor(omni_color, cv2.COLOR_BGR2RGB)
channels = cv2.split(omni_color_rgb)

# 处理每个通道
polar_channels = []
for ch in channels:
    ch_polar = map_coordinates(ch, [Y1.flatten(), X1.flatten()], order=1, mode='constant', cval=0)
    ch_polar = ch_polar.reshape((r_max, theta_max))
    polar_channels.append(ch_polar)

# 重组图像
omni_polar_color = cv2.merge(polar_channels)

# 显示结果
plt.figure(figsize=(8, 6))
plt.imshow(omni_polar_color.astype(np.uint8))
plt.title('彩色全景图像（极坐标变换）')
plt.axis('off')
plt.show()

# 比较灰度图像和彩色图像
fig, axs = plt.subplots(1, 2, figsize=(16, 6))

axs[0].imshow(omni_polar, cmap='gray')
axs[0].set_title('灰度全景图像')
axs[0].axis('off')

axs[1].imshow(omni_polar_color.astype(np.uint8))
axs[1].set_title('彩色全景图像')
axs[1].axis('off')

plt.tight_layout()
plt.show()

​

图 26：灰度和彩色转换图像的比较

​

通过分别处理每个颜色通道并将它们重新组合，我们在转换过程中保留了颜色信息。这使我们能够获得与源图像一致的彩色全景图像。

仿射变换

以下代码对图像 I 应用参数为 H 的单应变换，生成大小为 s = [Jh, Jw] 的图像 J。

def transformimage(I, H, s):
    Jh = s[0]
    Jw = s[1]
    X2, Y2 = np.meshgrid(range(Jw), range(Jh))
    X2 = X2.reshape(Jw * Jh)
    Y2 = Y2.reshape(Jw * Jh)
    invH = np.linalg.inv(H)
    X = np.zeros((Jh * Jw))
    Y = np.zeros((Jh * Jw))
    for i in range(Jw * Jh):
        P2 = np.array([X2[i], Y2[i], 1])
        P = invH.dot(P2)
        X[i] = P[0] / (P[2] + 1e-6)  # 避免除以零
        Y[i] = P[1] / (P[2] + 1e-6)
    X = X.reshape(Jh, Jw)
    Y = Y.reshape(Jh, Jw)
    J = np.zeros((Jh, Jw, I.shape[2]), dtype=I.dtype)
    for k in range(I.shape[2]):
        J[:, :, k] = scipy.ndimage.map_coordinates(I[:, :, k], [Y, X], order=1, mode='constant', cval=0)
    return J

a） 加载图像 lena256.png。应用该函数生成向量为 dx = +20, dy = +10 的平移，对应于以下单应矩阵：

#%% 问题 2a
# 加载图像
img = cv2.imread('lena256.png')
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 定义平移矩阵
H_translation = np.array([[1, 0, 20],
                          [0, 1, 10],
                          [0, 0, 1]])

# 定义输出图像的尺寸
s = [img_rgb.shape[0], img_rgb.shape[1]]

# 应用平移变换
transformed_translation = transformimage(img_rgb, H_translation, s)

b） 应用围绕点 ( x_0, y_0 ) = (100, 100) 的比例因子为 s = 0.4 的缩放变换，矩阵 H 如下：

其中:

c） 应用围绕点 ( x_0, y_0 ) = (100, 100) 的角度为 \alpha = 20^\circ 的旋转变换，矩阵 H 如下：

其中:

#%% 问题 2c
# 定义旋转矩阵
angle_deg = 20
a = np.deg2rad(angle_deg)
x0, y0 = 100, 100

HT = np.array([[1, 0, x0],
               [0, 1, y0],
               [0, 0, 1]])
HT_inv = np.linalg.inv(HT)
HR = np.array([[np.cos(a), -np.sin(a), 0],
               [np.sin(a), np.cos(a), 0],
               [0, 0, 1]])

H_rotation = HT.dot(HR).dot(HT_inv)

# 应用旋转变换
transformed_rotation = transformimage(img_rgb, H_rotation, s)

# 比较图像
fig, axs = plt.subplots(1, 4, figsize=(20, 5))

axs[0].imshow(img_rgb)
axs[0].set_title('原始图像')
axs[0].axis('off')
axs[1].imshow(transformed_translation.astype(np.uint8))
axs[1].set_title('平移变换')
axs[1].axis('off')
axs[2].imshow(transformed_scaling.astype(np.uint8))
axs[2].set_title('缩放变换')
axs[2].axis('off')
axs[3].imshow(transformed_rotation.astype(np.uint8))
axs[3].set_title('旋转变换')
axs[3].axis('off')

plt.tight_layout()
plt.show()

​

图 27：几何变换的比较

​

通过使用不同的仿射变换（平移、缩放、旋转），我们可以修改图像的位置、大小和方向。单应矩阵 H 允许根据所选参数精确控制这些变换。

单应变换

a） 定义 pts1 为源图像角点的坐标（顺序：左上角、右上角、左下角、右下角）：

# 问题 3：单应变换
# a）定义源图像和目标图像的角点

s = img_rgb.shape
pts1 = np.float32([[0, 0], [s[1], 0], [0, s[0]], [s[1], s[0]]])

b） 应用单应变换，将图像的四个角映射到用户选择的位置，并定义 pts2 为目标图像中的对应坐标（尺寸 Jh \times Jw = 256 \times 256）。

# 定义目标坐标
Jh, Jw = 256, 256
pts2 = np.float32([[50, 50], [Jh - 50, 30], [30, Jw - 50], [Jh - 50, Jw - 50]])

c） 使用 getPerspectiveTransform 函数以矩阵 H 的形式计算单应变换参数。应用此矩阵转换图像。显示获得的图像，并在图像上叠加 pts2 点。

#%% b）计算单应变换并应用

# 计算单应变换矩阵
H_perspective = cv2.getPerspectiveTransform(pts1, pts2)

# 应用变换
transformed_perspective = cv2.warpPerspective(img_rgb, H_perspective, (Jw, Jh))

# 显示结果
fig, axs = plt.subplots(1, 2, figsize=(16, 6))

axs[0].imshow(img_rgb)
axs[0].set_title('原始图像')
axs[0].axis('off')
axs[1].imshow(transformed_perspective.astype(np.uint8))
axs[1].scatter(pts2[:, 0], pts2[:, 1], c='red', marker='o')
axs[1].set_title('单应变换的结果')
axs[1].axis('off')

plt.tight_layout()
plt.show()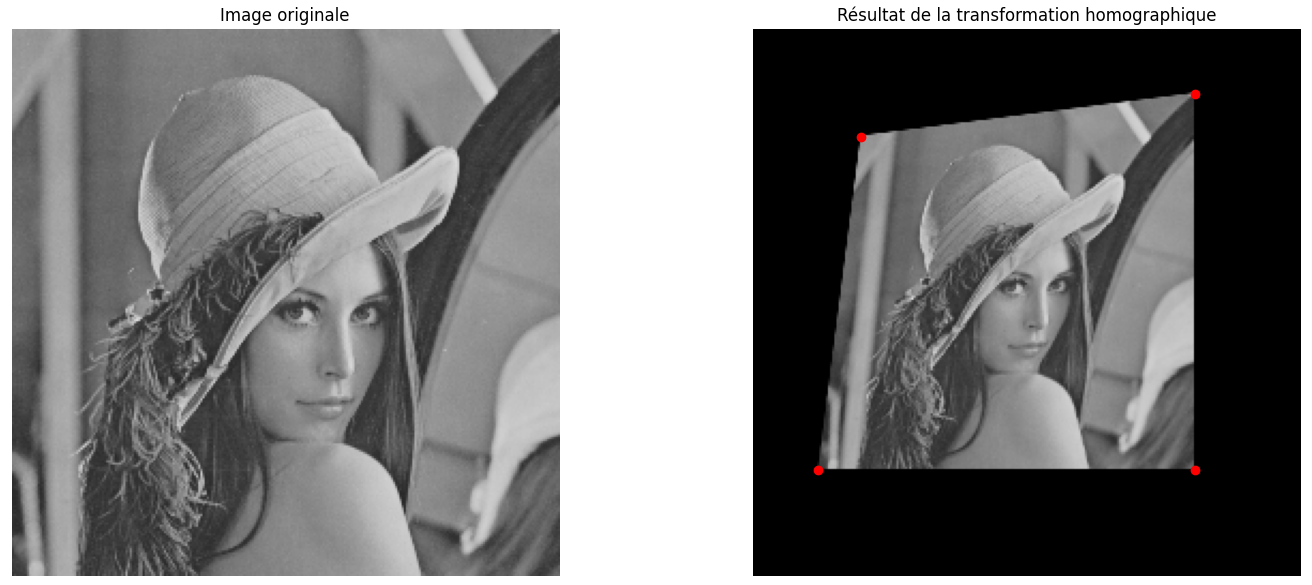

图像 29：应用单应变换

​

单应变换允许使用描述对应点关系的矩阵 H 将一个平面转换为另一个平面。这在透视校正或不同视图之间的映射中特别有用。这部分的具体理论公式见 3D重建理论