傅里叶综合
编辑背景介绍
厄米特(Hermitian)对称矩阵
首先,我们讨论复矩阵和共轭转置的基本概念。对于一个复元素矩阵 M,我们定义它的共轭转置为
其中 M^{\top} 表示转置, M^\ast 表示取复共轭。如果 M=M^\dagger,则称 M 是厄米特(Hermitian)对称矩阵。当矩阵元素均为实数时,有M^\dagger = M^{\top}。
梯度和 Hessian 矩阵: 设M 是一个N \times N 的厄米特对称方阵, m 是一个大小为N 的向量。定义两个从\mathbb{C}^N 到\mathbb{R} 的映射\varphi 和\psi,对于任意u \in \mathbb{C}^N:
它们都是二次可微的。它们的梯度分别为:
它们的 Hessian 矩阵分别为:
这是二次型在优化问题中求极值点时梯度和Hessian 矩阵的经典表达式。
核磁共振成像(MRI)图像重建
接下来,我们介绍核磁共振成像(MRI)图像重建问题。MRI 利用测量傅里叶变换系数来获取图像信息,但由于实际采集中只能获得部分频率信息,加上噪声的干扰,问题就变成了一个病态问题。具体来说,我们无法获取完整的傅里叶系数,因此在频率域中高频或低频信息可能缺失,导致重建图像时整体结构或者细节信息丢失,从而产生伪影、失真或者模糊现象。所以从图像重建所涉及的数据处理角度来看,该问题属于"傅里叶综合"问题的范畴
这里就有第一个概念问题,为什么傅立叶变换系数可以描述图像信息?它们之间有什么数学联系?
傅立叶变换可以讲图像从空间域转换到频率域,把空间域中的每个点都视作频率域中不同频率成分的叠加(或者说将图像分解成一系列不同频域的分量),而傅立叶变换系数正好描述了这些正弦波/余弦波的幅值和相位。比如说我们有一个空间域信号 x ,我们对其进行傅立叶变换 \overset{\circ}{x}=F x,这里的 \overset{\circ}{x} 就是频域表示,在数学上这个结果是一个复数函数
A(f) 是振幅, \phi(f) 是相位
因此我们希望得到完整的傅立叶系数集合(k 空间数据),但在MRI中实际测量结果是部分傅立叶系数,这就导致部分对应频率信息缺失,重建就变成了一个病态的反问题。
这里有第二个概念,k 空间数据是一个什么样式的数据分布?
k 空间数据通常以二维/三维数组形式存在,其中的每个元素 k(x,y) 或 k(x,y,z) 都是一个复数,代表着对应空间频率(或波数)的振幅和相位信息,在我们的 MRI 问题中, k 空间数据就是我们通过测量直接获得的频域数据,也就是图像的傅立叶变换系数。之前说过由于种种原因,获取到的k 空间数据往往是不完整的,这正是导致图像重建问题病态的一个关键原因。
我们下面直观的展示一下这个流程和对应结果:
%% 示例 MATLAB 代码:从空间域到频率域,再到部分采样重建
% 1. 读取图像(使用 MATLAB 自带的 "cameraman.tif" 图像)
img = imread('cameraman.tif');
img = double(img); % 转换为 double 类型便于计算
% 2. 对图像进行二维傅里叶变换
F = fft2(img);
% 为了直观显示,将低频移到图像中心
Fshift = fftshift(F);
% 3. 计算傅里叶变换的振幅和相位
magF = abs(Fshift);
phaseF = angle(Fshift);
% 4. 绘制原始图像、傅里叶振幅(取对数后更直观)、相位以及3D网格图
figure;
subplot(2,2,1);
imshow(uint8(img));
title('原始图像');
subplot(2,2,2);
% 对数尺度显示振幅,防止数值差异过大
imagesc(log(1+magF));
colormap gray; axis image;
title('傅里叶振幅谱 (对数尺度)');
subplot(2,2,3);
imagesc(phaseF);
colormap gray; axis image;
title('傅里叶相位谱');
subplot(2,2,4);
mesh(log(1+magF));
title('3D 网格图:对数振幅');
% 5. 模拟部分 k 空间采样
% 构造一个采样掩模 T,假设只采样图像中心 30% 区域(即低频部分)
[n1, n2] = size(img);
mask = zeros(n1, n2);
rowRange = round(n1*0.35):round(n1*0.65);
colRange = round(n2*0.35):round(n2*0.65);
mask(rowRange, colRange) = 1;
% 将采样掩模应用于傅里叶变换(注意:Fshift 已经中心化)
Fmask = Fshift .* mask;
% 6. 利用部分采样的 k 空间数据进行零填充重建
% 首先将部分数据反中心化,再做逆傅里叶变换
Fmask_unshift = ifftshift(Fmask);
img_recon = real(ifft2(Fmask_unshift));
% 7. 绘制采样掩模、部分 k 空间数据和重建图像
figure;
subplot(2,2,1);
imagesc(mask);
colormap gray; axis image;
title('采样掩模 T');
subplot(2,2,2);
imagesc(log(1+abs(Fmask)));
colormap gray; axis image;
title('部分 k 空间 (对数振幅)');
subplot(2,2,3);
imshow(uint8(img_recon));
title('零填充重建图像');
subplot(2,2,4);
imshow(uint8(img));
title('原始图像对比');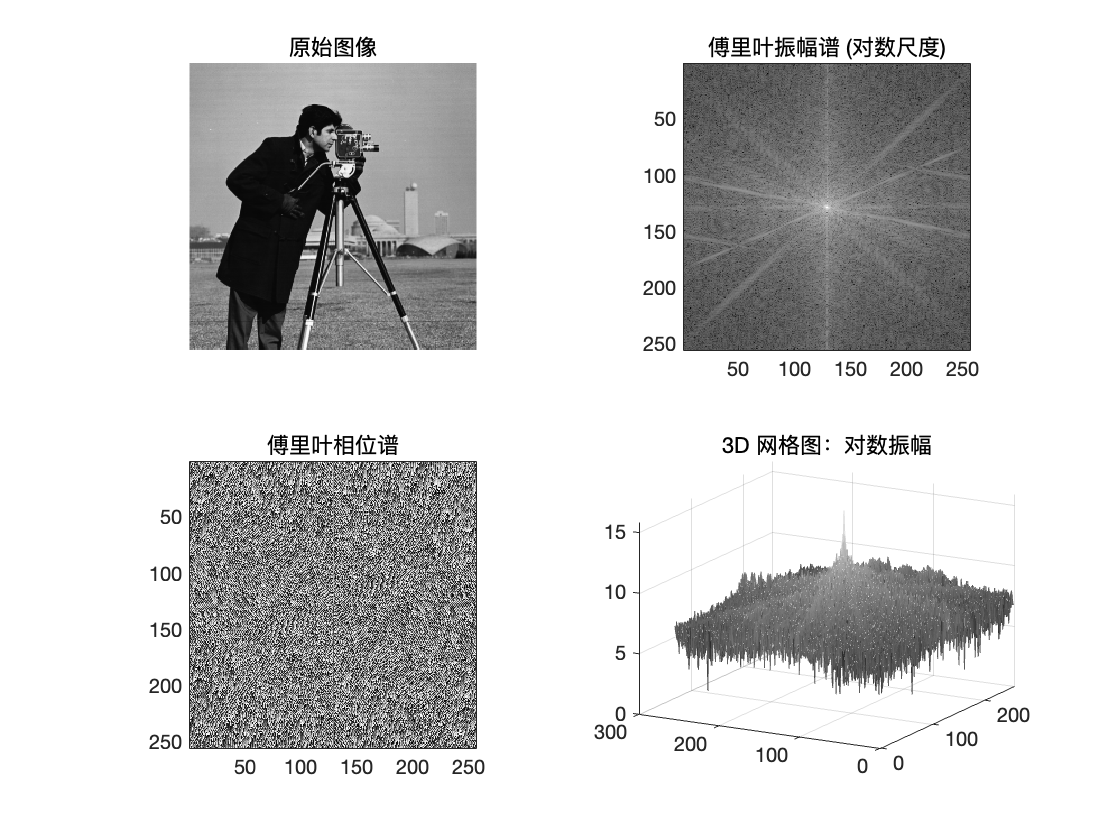

代码首先读取一幅灰度图像,然后 fft2 和 fftshift 标准操作,利用 abs 和 angle 分别计算傅里叶变换的振幅和相位。对数变换 (log(1+⋅))用于显示振幅谱,使得低振幅部分也能清晰显示, mesh 绘制了对数振幅的三维网格图,直观不同频率成分的强度分布。
随后我们构造了一个采样掩膜 T ,用它对傅立叶结果进行截断来模拟 MRI 病态问题的观测,然后 经过 ifft 操作后观察重建图像,可见高频信息丢失,细节损失。这就是我们的 MRI 病态问题。
频率的不均匀观测在重建图像中的体现
频率的不均匀观测导致重建图像中缺失某些频率成分。如果低频信息缺失,图像的整体结构信息会丢失;如果高频成分缺失,图像会变得模糊。此外,这可能导致图像中亮度和对比度的不均匀,或者产生伪影和失真。
一维傅立叶综合问题描述
在实际应用中,FS 问题一般用在二维或三维域上。这里为了展开理论分析,我们在一维域上处理它。数学上,我们可以将问题表述为:
其中:
y \in \mathbb{C}^M 是包含M 个观测数据的向量, x \in \mathbb{C}^N 是包含N 个未知数的向量, e \in \mathbb{C}^M 是包含M 个测量误差的向量。
F 是归一化的 DFT(离散傅里叶变换)矩阵: F^\dagger F = F F^\dagger = I,其中I 是大小为N 的单位矩阵。此外,它是一个对称矩阵, F^{\top} = F。
T 是截断矩阵:它从F x 中提取被观测到的傅里叶系数,丢弃未被观测到的。例如,如果N = 8, M = 3,系统只观测第 1、第 2 和第 4 个系数,那么有:
不同情况下的讨论
如果所有系数都被观测到或者只观测到每两个系数中的一个,对应矩阵T 的表达式如下:
(1) 如果所有N 个傅里叶系数都被观测到,那么M = N。因此,矩阵T 是一个N \times N 的单位矩阵I_N:
(2) 如果只观测到每两个系数中的一个(即观测位置为1, 3, 5, \dots 的系数),那么M = \frac{N}{2}(假设N 为偶数), T 是一个\frac{N}{2} \times N 的矩阵,在对应于被观测到的傅里叶系数的位置上为 1,其余为 0:
前置计算
接下来我们计算矩阵T^{\top} T, T T^{\top} 和向量\bar{y} = T^{\top} y。
以N = 8, M = 3,观测位置在第 1、第 2 和第 4 个系数为例:
则有:
矩阵T^{\top} T 为:
矩阵T T^{\top} 是一个3 \times 3 的单位矩阵I:
向量\bar{y} 为:
这实际上是在对应于被观测到的傅里叶系数的位置上放置观测数据,其余位置为零。
特殊情况分析
现在我们令x_0 \in \mathbb{C}^N 为一种特殊情况,x = F^\dagger (I - T^{\top} T) F x_0。对于此x,我们给出包含观测数据的y 的表达式:
首先,计算F x:
然后,
由于T T^{\top} = I,因此:
在这个特殊情况构造下,无论 x_0 如何(即使存在),观测数据 y 完全丢失了关于 x_0 的信息,只剩下噪声 e,这说明了在数据不完整的情况下,存在一个特殊的 x,使得我们根本无法用观测数据y 来重建x_0。
03/03
傅里叶综合、内插-外推 和卷积
我们借助变量替换\overset{\circ}{x} = F x,来证明 FS 问题 的确可以被表述为一个“内插-外推”问题。
首先使用替换\overset{\circ}{x} = F x,则有:
由于我们只观测到了部分傅里叶系数(内插),任务是估计完整的傅里叶系数集(外推)。这涉及对未知的傅里叶系数进行插值和外推,即在给定某些点的值的情况下,估计其他点的值,这是一个插值问题的本质。
然后我们再令\tilde{x} = F^\dagger \bar{y}。并计算出\tilde{x} 和x 之间的关系,以此来推导出 FS 问题也可以被表述为一个反卷积问题。
首先, \bar{y} = T^{\top} y,因此:
由于y = T F x + e,代入得:
因为F^\dagger T^{\top} T F 是一个线性算子作用于x,所以可以写成:
其中\tilde{e} = F^\dagger T^{\top} e。
这表明傅里叶综合问题也可以被视为一个反卷积问题,其中F^\dagger T^{\top} T F 充当卷积矩阵。
因此反卷积任务 是从被模糊的信号\tilde{x} 中恢复原始信号x,其中模糊是由系统函数F^\dagger T^{\top} T F 引起的。
经验估计
针对以上问题,我们提出一个x 的经验估计量\hat{x}_E,可以定义为:
即将未观测到的傅里叶系数设为零,用\bar{y} 替换完整的傅里叶系数集,然后通过逆傅里叶变换获得x 的估计。
我们让\overset{\circ}{x}_E = F \hat{x}_E
由于\hat{x}_E 是\tilde{x},其表达式为:
这解释了为什么它可以被视为一个反卷积问题。在这种情况下,卷积导致图像模糊,细节丢失,分辨率下降。因此,由于傅里叶系数的不完整,经验估计量导致图像分辨率较低。
最小二乘估计方法
我们尝试使用最小二乘(LS)方法估计x。我们从公式 (4) 引入一个准则J_{\text{LS}}:
J_{\text{LS}} 没有唯一的极小值点
证明
对J_{\text{LS}}(x) 求导:
解得:
即:
由于T 只观测部分傅里叶系数,这意味着矩阵T F 是秩亏的。因此,方程T F x = y 没有唯一解。这表明仅使用最小二乘方法无法获得x 的唯一估计,需要引入正则化项以改善解的唯一性。
我们再计算J_{\text{LS}}(\tilde{x})
由于\tilde{x} = F^\dagger \bar{y} = F^\dagger T^{\top} y,则:
准则达到最小值 0,但这并不意味着\tilde{x} 是原始信号的正确重建,表明仅使用最小二乘方法无法获得正确的唯一解。
带惩罚的最小二乘估计方法
现在我们尝试使用带惩罚的最小二乘(PLS)方法估计x。我们引入一个惩罚项P,考虑到x 的连续样本之间的差异(在循环情况下,即x_{N+1} = x_1)
首先构建相应的 PLS 准则J_{\text{PLS}}
其中\mu 是正则化参数,控制惩罚项的权重。
矩阵D 的形式为:
D 是一个N \times N 的循环差分矩阵,用于计算x 中相邻元素的差值。
\mu 控制数据拟合项和平滑惩罚项之间的平衡:
当\mu 较大时,惩罚项权重较高,更多地抑制高频噪声,但可能使图像细节模糊。
当\mu 较小时,更侧重于数据拟合,但可能过度拟合噪声。
最小化J_{\text{PLS}}(x),有:
对x 求导并令导数为零:
解得:
因此,
我们令\overset{\circ}{x} _{\text{PLS}} = F \hat{x} _{\text{PLS}}
由于F F^\dagger = I,并且F D F^\dagger 可以对角化D,因此有:
当\mu \rightarrow 0 时,正则化项的影响消失,回到最小二乘准则。此时,解可能不唯一,且容易受到噪声影响。
当\mu \rightarrow +\infty 时,惩罚项的权重极大,所有的频率成分都被抑制,分辨率极低,图像过于平滑,细节完全丢失。
时代不一样了,现在都用深度学习的方法,如卷积神经网络CNN,来自动提取数据特征,从而重建高分辨率的图像。缺点是训练数据要多,学习从不完整或受噪声污染的数据中恢复细节的能力,显著提高图像的分辨率和质量。