反问题: 凸正则化与轮廓感知
编辑之前的工作已经涉及维纳-亨特方法,本次实验则提出 Huber正则化方法,也叫做 半二次(Half-Quadratic)正则化方法
WIENER - HUNT方法回顾
我们使用以下数学模型来描述获取过程:
其中,向量y 表示观察到的数据(模糊图像),向量x 表示未知的真实图像(清晰图像), H 是卷积矩阵,e 是表示测量和建模误差的向量。
为了对去卷积问题进行正则化,我们需要引入图像二维空间的附加信息,最简单的方法是 使用相邻像素灰度差,并将其作为惩罚。因此带惩罚的准则形式如下:
其中势函数\varphi_Q(\delta) = \delta^2
我们可以将其中相邻像素差 x_p - x_q 重写为差分矩阵的形式 D :
该准则的最小化值就是我们要的重构的图像\hat{x}_Q :
经过一通处理,我们找到最小值:
之前讲过这个求逆玩不了,因此引入循环近似方法,在傅里叶基下对循环矩阵进行对角化。这样可以以较低的计算成本计算解,即Wiener - hunt 解法。可见,这种循环近似的思想在高维矩阵求逆的情况下非常好用,我们同样接下来也会用这个技巧。
给定适当选择的 \mu 值,我们可以看到明显的去卷积效果。然而,分辨率和恢复锐利边缘的能力有限,不能很好地处理恢复图像中的灰度突变。本次实践作业的目的是克服这一限制。
凸正则化
2.1 Huber势函数
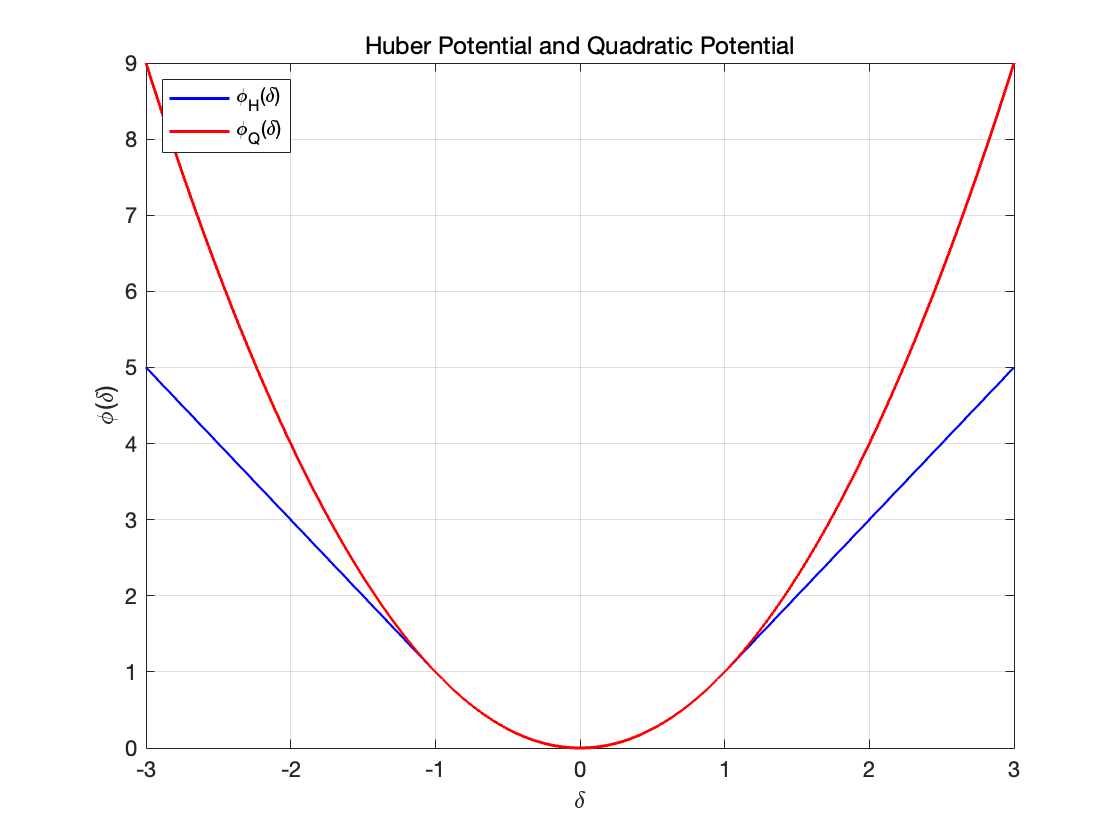
为了进一步提高分辨率并具有更好的边缘保护特性,我们重新考虑势函数 ϕ,例如:
这被称为Huber势函数。它在阈值 T 之前具有二次行为,而在阈值 T 之后呈现线性行为
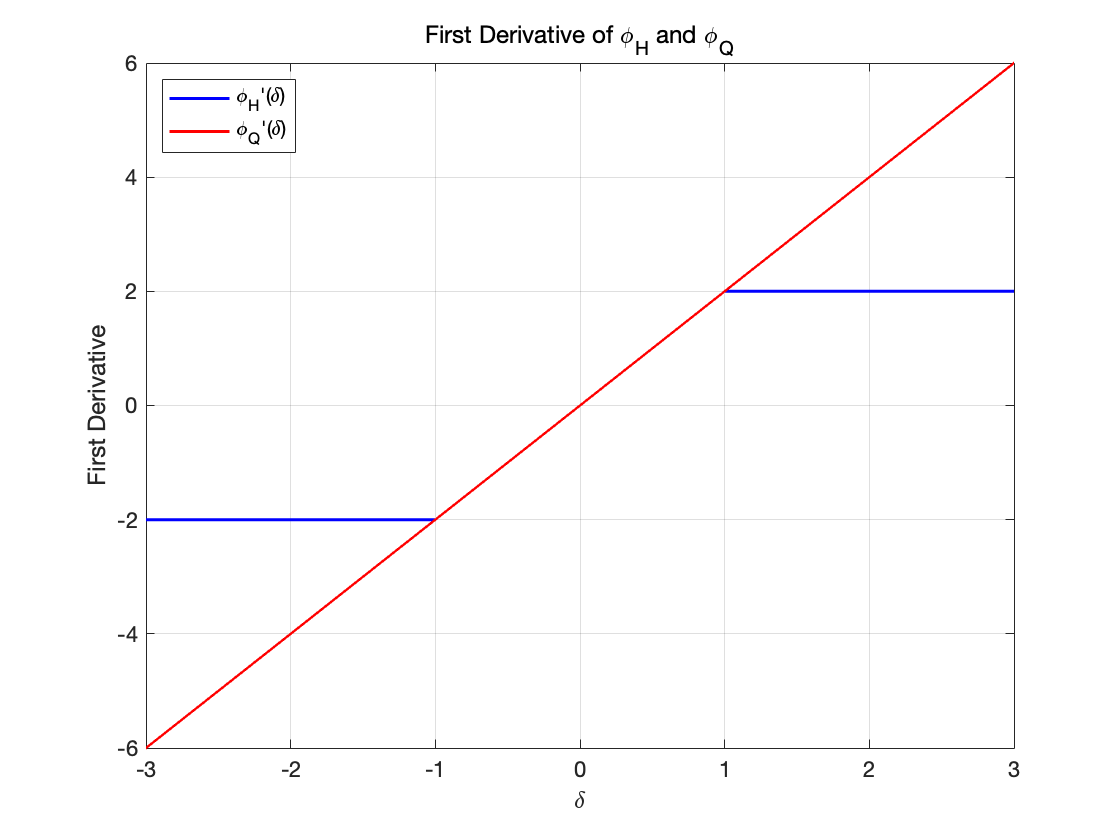
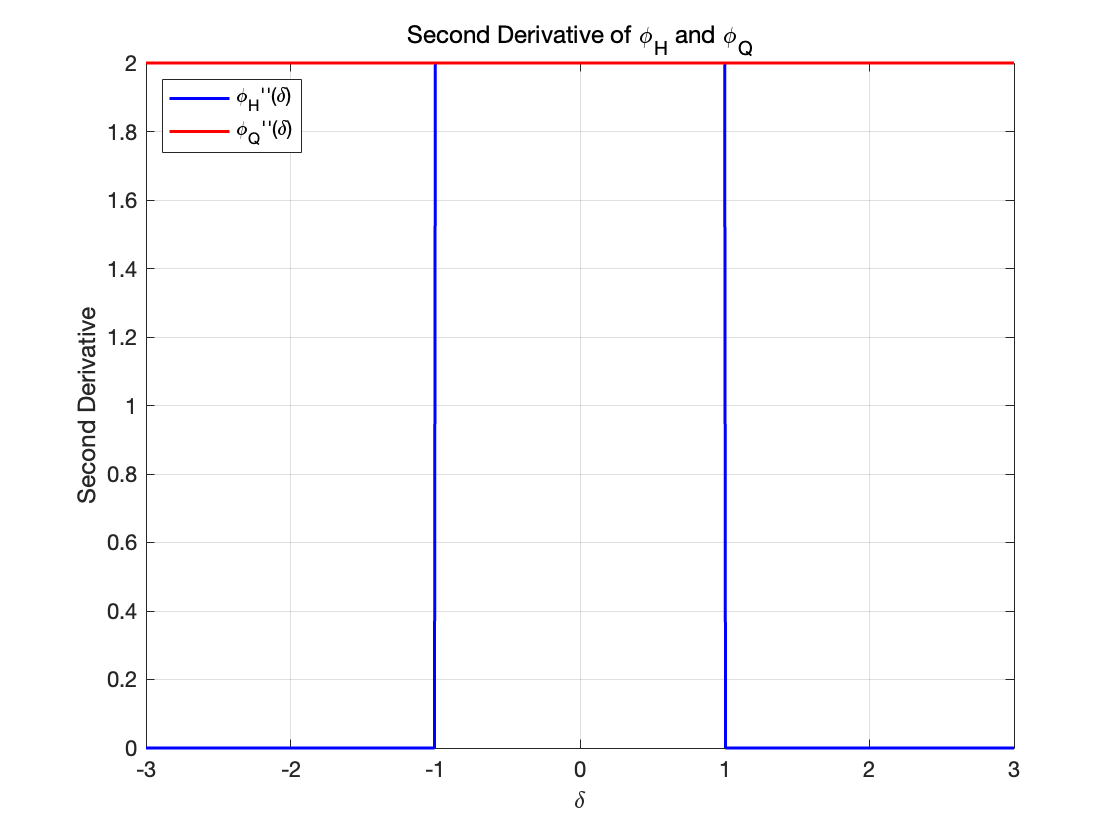
对于\varphi_H的导数(蓝线):
对于\varphi_Q(\delta) = \delta^2 的导数(红线):
从Huber势函数\varphi_H 开始,我们定义了一个与(1)中给出的准则相似的新准则:
上述新准则的最小化解就是新恢复的图像\hat{x}_H :
那么新的势函数\varphi_H 与之前的势函数\varphi_Q 相比其优势在哪里呢?
新的势函数\varphi_H 能够更好地保护边缘,因为它在大于某个阈值T 时呈现线性增长,而不是像\varphi_Q(\delta) = \delta^2 这样呈现二次增长,即当梯度较大(边缘)时,平方后惩罚项迅速增加,导致算法倾向于减小这些梯度。线性增长比二次增长更加平缓,可以降低梯度增加的速度,防止边缘被过度平滑,利于保护边缘信息。
重新回到之前新势函数的定义
其中阈值T 决定了势函数\varphi_H(\delta) 何时从二次增长切换为线性增长
如果像素之间的差异|\delta| 超过了阈值T,意味着应该是图像中的边缘部分 。此时, \varphi_H(\delta) 将从二次惩罚转为线性惩罚 ,对 边缘 施加的惩罚就更小,从而更好地保留图像中明显的特征和细节
当像素差异较小时 (|\delta| < T),\varphi_H(\delta) 的行为与传统的二次势函数\varphi_Q(\delta) = \delta^2 相同
我们注意,所选择的 \varphi_H 函数是凸的,我们推断整个准则J_H 也是凸的,因此它有一个唯一的最小值。我们下面也可以推导证明这一点。
由于算法的原因,我们引入了一个额外的参数\alpha,一个严格正的实数。惩罚项乘以并除以\alpha,并令\mu^{\prime} = \mu / \alpha ,整个公式是不变的:
\alpha 的值影响了梯度下降中每一步的更新幅度,较小的\alpha 保守,较大的\alpha 可能振荡
通过调整\alpha,可以间接控制\mu’ 的大小(后续),进而改变数据项和正则化项的平衡
2.2 优化
下面计算新准则 J_H 的最小值,与二次准则(1)J_Q 不同,我们无法直接通过解析式求解最小值,但可以通过数值迭代算法来计算其唯一最小化值。然后,我们要引入辅助变量,这样才能够在傅里叶基下利用 Wiener - Hunt 解法高效地进行计算。
2.2.1 扩展准则与辅助变量
为了在循环近似下重复使用二次情况( Wiener - Hunt 解)的结果,我们引入了一组新的变量,称为辅助变量。更具体地说,我们为每对相邻像素(p, q) 引入一个变量a_{pq},并将所有这些新变量收集到向量a 中。
我们对准则(3)进行了扩展,原准则(3)形式如下:
我们构造一个函数,\alpha \varphi(\delta) ,其定义为
那么,\alpha \varphi_H(x_p - x_q) 为:
所以新准则(4)形式如下:
这是关于未知图像 x 和辅助变量a 的函数。它分为三部分:
最小二乘项|y - Hx|^2
涉及像素差异和辅助变量的二次项\left( (x_p - x_q) - a_{pq} \right)^2
仅涉及辅助变量的函数项\tilde{\zeta}_\alpha ,我们称它为辅助函数项
构建的关键是通过最小化扩展准则\tilde{J}_H(x, a) 来最小化原始准则J_H(x),即:
我们现在已经搞定了最小二乘项,像素差异项可以用差分矩阵然后循环近似搞定,现在唯一棘手的东西就是这个 \tilde{\zeta} _\alpha , 因此如何设计\tilde{\zeta} _\alpha 对于上述思想的成立至关重要,我们需要用到凸对偶性和 Legendre-Fenchel Transform理论,结论是它证明了\tilde{\zeta} _\alpha 也是Huber函数。
回顾 Huber函数 的定义:
\tilde{\zeta} _\alpha 表达式:
我们需要证明:
我们需要满足:
\tilde{\zeta}_\alpha(a) 是\alpha \varphi_H(\delta) 的凸对偶形式。
给定\alpha \varphi_H(\delta) 的表达式,利用凸对偶和 Legendre-Fenchel Transform理论推出\tilde{\zeta}_\alpha(a)。
Huber函数\varphi_H(\delta) 定义如下:
扩展后乘以\alpha:
利用定义:
等价于寻找满足以下关系的\tilde{\zeta}_\alpha(a):
这就是 Legendre-Fenchel Transform。
根据\alpha \varphi_H(\delta) 的分段定义,我们需要分别考虑|\delta| \leq T 和|\delta| > T 两种情况。
情况 1:|\delta| \leq T
需要求解:
展开括号:
导数为零求极值:
解得:
验证取值范围:
当 |a| \leq (1 - 2\alpha)T,\delta^* 落在[-T, T] 内,因此没问题。
将\delta^ * 代入原表达式:
化简为:
情况 2: |\delta| > T
需要求解:
令g(\delta)=2\alpha T|\delta| - \alpha T^2 - \frac{1}{2}(\delta - a)^2,对g(\delta) 求导数:
当\delta > 0 时:
当\delta < 0 时:
将\delta^* 代入并考虑边界条件,最终得到:
将两种情况的结果合并,得到\tilde{\zeta}_\alpha(a) 的最终表达式:
证明完毕
参数\alpha \in \left(0, \frac{1}{2}\right) ,在此范围能够对算法进行精细调整,它只影响优化算法性质例如收敛速度,和我们最终结果无关。
2.2.2 求最小值
我们重新回到准则 (3),新准则的提出有一个重要思想:
表明我们可以通过 x 和a 的联合最小化\tilde{J}_H(x, a) 来得到J_H(x) 的最小化值:
从编程的角度来看,我们将通过迭代两步过程来计算\tilde{J}_H(x, a) 关于x 和a 的联合最小化,直到收敛:
其中,\tilde{x}_H 就是我们想要的J_H(x) 的最小化值\hat{x}_H
为了计算这个联合最小化解,我们将通过迭代两步过程来实现\tilde{J}_H(x, a) 关于x 和a 的联合最小化,直到收敛:
① 对于固定的a,最小化\tilde{J}_H(x, a) 来更新x,这将得到\bar{x}(a) = \arg \min_x \tilde{J}_H(x, a)
② 对于固定的x,最小化\tilde{J}_H(x, a) 来更新a,这将得到\bar{a}(x) = \arg \min_a \tilde{J}_H(x, a)
通过这样的迭代过程,我们可以找到最终的最优解\hat{x}_H = \tilde{x}_H,即最优的图像恢复结果。迭代的本质是分步优化,在每一步中只优化一个变量 ( x 或a),这比直接联合优化两个变量要简单得多。
现在我们给出步骤 ① 的显式解,并通过循环近似高效地计算它。
在固定\alpha 的情况下,最小化扩展准则\tilde{J}_H(x, \alpha) 关于x:
由于\zeta _{\alpha}(a _{pq}) 不包含x,在对x 进行最小化时,可以暂时忽略该项。因此,目标函数关于x 可写为:
我们引入差分算子 D,将所有像素对的项表示为范数形式:
为求解最优x,我们对准则关于x 求导并令其为零,即
得到:
整理得到:
同样的问题,很难通过直接矩阵计算来得到解析解,因此将卷积矩阵 H 和差分算子 D 近似为循环矩阵,可以在频域中同时对角化。
2.2.3 近似循环矩阵的对角化
循环矩阵可以通过离散傅里叶变换(DFT)进行对角化:
其中:
F 是离散傅里叶变换矩阵, F^{\dagger} 是其共轭转置。
\Lambda_H 和\Lambda_D 是对角矩阵,其对角元素为对应循环矩阵的特征值。
回到之前的最优解公式:
H 和D 被替换为\tilde{H} 和\tilde{D},于是:
循环矩阵的转置等于其共轭转置,即\tilde{H}^T = \tilde{H}^\dagger,同理\tilde{D}^T = \tilde{D}^\dagger。
将方程两边左乘F,并利用F F^\dagger = I 的性质,有:
其中\hat{x} = Fx
由于F \tilde{H}^\dagger \tilde{H} F^\dagger = |\Lambda_H|^2
并且F \tilde{H}^\dagger y =F \tilde{H}^\dagger F^\dagger F y = \Lambda_H^* \hat{y}
因此,频域中的方程变为:
解上述方程,得到最小值:
如果我们不严谨一点,只注重美观,我们可以写成如下形式
因为 \Lambda_H 和\Lambda_D 是矩阵所以这么写多少有点问题,写逆严谨一点。
扩展:
如果我们进一步更细一点,在二维图像中,差分算子 D 包括水平和垂直方向的梯度:
对应的傅里叶变换为:
将差分算子的水平和垂直分量代入,得到:
其中\hat{a}_h, \hat{a}_v 分别是辅助变量a 在水平方向和垂直方向上的傅里叶变换。
计算完\hat{x} 后,通过逆傅里叶变换得到空间域的x:
当a = 0 时,问题退化为经典的维纳-亨特去卷积问题。此时,辅助变量a 的正则化效应消失,算法只剩下标准的二次型最小化问题。
虽然能简单地得到去卷积解,但无法利用半二次方法的优势来更好地处理边缘。
则频域解变为:
或者表达成:
接下来我们着重处理步骤 ② ,我们可以独立并行更新每个a_{pq} ,为什么?
在扩展准则\tilde{J} _H(x, \alpha) 中,涉及辅助变量a _{pq} 的部分为:
每个a_{pq} 仅与对应的像素差异(x_p - x_q) 和自身相关,而与其他像素对无关。因此,每个a_{pq} 的更新是相互独立的,只需考虑对应的像素对,这使得我们可以并行更新所有的辅助变量a_{pq},而不需要等待其他像素对的计算结果,从而提高计算效率。
接下来我们看辅助变量a_{pq} 的两种设计方式,作为像素间差异\delta_{pq} = x_p - x_q 的函数
通过上述公式推导:
课堂讲义中期望的解:
其中\varphi'_H(\delta) 是 Huber 势函数的导数:
两者是相同的。在实现时可以直接使用第二种方式。
证明两种设计方案是相同的
情况 1:
当 \delta_{pq} \geq T 时,
将其代入方法 2 的公式:
情况 2:
当 -T \leq \delta_{pq} \leq T 时,
将其代入方法 2 的公式:
情况 3:
当 \delta_{pq} \leq -T 时,
将其代入方法 2 的公式:
这与方法 1 中的公式完全一致,证明完毕。
这种半二次方法的优点在于,步骤①和②都是显式的,而直接最小化 J_H(x) 则不是。该算法也可以以下列形式给出。
下面我们给出这种半二次算法的迭代更新步骤,我么 可见其步骤步骤①和②都是显式的,比直接最小化 J_H(x) 方便的多:
初始化 a^{[0]} = 0
对于k = 1, 2, \dots 重复如下 1、2 步骤:
我们将结果与使用维纳-亨特方法得到的结果进行比较
对比结果:
Wiener-Hunt 方法:采用二次正则化,倾向于全局平滑, 导致边缘模糊。
Huber 正则化方法:在平滑区域与二次正则化效果相似,但在边缘处惩罚减小,保留边缘细节。
参数\mu 的影响:
较大的 \mu:正则化项权重增加,无噪声,图像更平滑,细节丢失。
较小的 \mu :正则化项权重减小,有噪声,但边缘和细节保留更好。
参数T 的影响:
较大的 T:边缘保护减弱,无噪声,图像更平滑,细节丢失。
较小的 T :更多的像素差异被视为边缘,有噪声,但边缘和细节保留更好。
因此我们要调整 \mu 和 T 来找到一个平衡点
clear all
close all
clc
%% question 6a (从此开始)
% ----------------------------
% Step 1: 加载数据
% ----------------------------
Data = load('DataTwo.mat');
ObservedImage = Data.Data;
TrueImage = Data.TrueImage;
IR = Data.IR;
[M, N] = size(ObservedImage);
Long = max(M, N);
Nu = linspace(-0.5, 0.5, Long);
% ----------------------------
% Step 2: 定义参数
% ----------------------------
mu_huber = 0.01; % Huber 正则化的参数
T = 1; % Huber 函数阈值
alpha = 0.4; % 辅助变量参数
epsilon = 1e-4; % 收敛阈值
max_iter = 100; % 最大迭代次数
% ----------------------------
% Step 3: 生成频率轴并预处理
% ----------------------------
TF_ObservedImage = MyFFT2(ObservedImage);
TF_IR = MyFFT2RI(IR, Long);
% ----------------------------
% Step 4: 定义正则化滤波器(差分算子)
% ----------------------------
D_c = [0 0 0; 0 -1 1; 0 0 0]; % 水平方向差分
D_r = D_c'; % 垂直方向差分
FT_D_c = MyFFT2RI(D_c, Long);
FT_D_r = MyFFT2RI(D_r, Long);
abs_Dc_squared = abs(FT_D_c).^2;
abs_Dr_squared = abs(FT_D_r).^2;
% ----------------------------
% Step 5: 初始化辅助变量
% ----------------------------
a_C = zeros(M, N); % 水平方向的辅助变量
a_R = zeros(M, N); % 垂直方向的辅助变量
x = ObservedImage;
x_prev = x;
k = 0;
factor = mu_huber/(2*alpha);
% ----------------------------
% Step 6: 主循环 - Huber 正则化优化
% ----------------------------
while k < max_iter
k = k + 1;
% Step 6a: 更新 x
TF_a_C = MyFFT2(a_C);
TF_a_R = MyFFT2(a_R);
Numerator = conj(TF_IR).*TF_ObservedImage + factor*(conj(FT_D_c).*TF_a_C + conj(FT_D_r).*TF_a_R);
Denominator = abs(TF_IR).^2 + factor*(abs_Dc_squared + abs_Dr_squared);
Denominator( Denominator == 0 ) = 1e-12; % 防止除零
TF_x = Numerator ./ Denominator;
x = MyIFFT2(TF_x);
% Step 6b: 更新 a
delta_C = MyIFFT2(FT_D_c .* TF_x);
delta_R = MyIFFT2(FT_D_r .* TF_x);
% huber_derivative inline
phi_prime_C = zeros(size(delta_C));
mask_C = abs(delta_C) <= T;
phi_prime_C(mask_C) = 2 * delta_C(mask_C);
phi_prime_C(~mask_C) = 2 * T * sign(delta_C(~mask_C));
phi_prime_R = zeros(size(delta_R));
mask_R = abs(delta_R) <= T;
phi_prime_R(mask_R) = 2 * delta_R(mask_R);
phi_prime_R(~mask_R) = 2 * T * sign(delta_R(~mask_R));
a_C = delta_C - alpha * phi_prime_C;
a_R = delta_R - alpha * phi_prime_R;
% 收敛判断
dx = norm(x - x_prev,'fro') / (norm(x_prev,'fro')+1e-12);
if dx < epsilon
disp('Algorithm converged.');
break;
end
x_prev = x;
end
% ----------------------------
% Step 8: 计算指标(MSE 和 PSNR)
% ----------------------------
mse_huber = mean((TrueImage(:) - x(:)).^2);
% psnr_custom inline for x
if mse_huber == 0
psnr_huber = Inf;
else
max_pixel_huber = max(x(:));
psnr_huber = 10 * log10((max_pixel_huber^2) / mse_huber);
end% ----------------------------
% Step 9: 显示结果
% ----------------------------
figure;
subplot(1,3,1); imagesc(ObservedImage); colormap gray; axis off; title('Observed');
subplot(1,3,2); imagesc(TrueImage); colormap gray; axis off; title('True');
subplot(1,3,3); imagesc(x); colormap gray; axis off; title('Huber Reg');
fprintf('Difference Metrics:\n');
fprintf('-------------------\n');
fprintf('Huber Regularization Method (mu = %.2f):\n', mu_huber);
fprintf('MSE: %.6f\n', mse_huber);
fprintf('PSNR: %.2f dB\n', psnr_huber);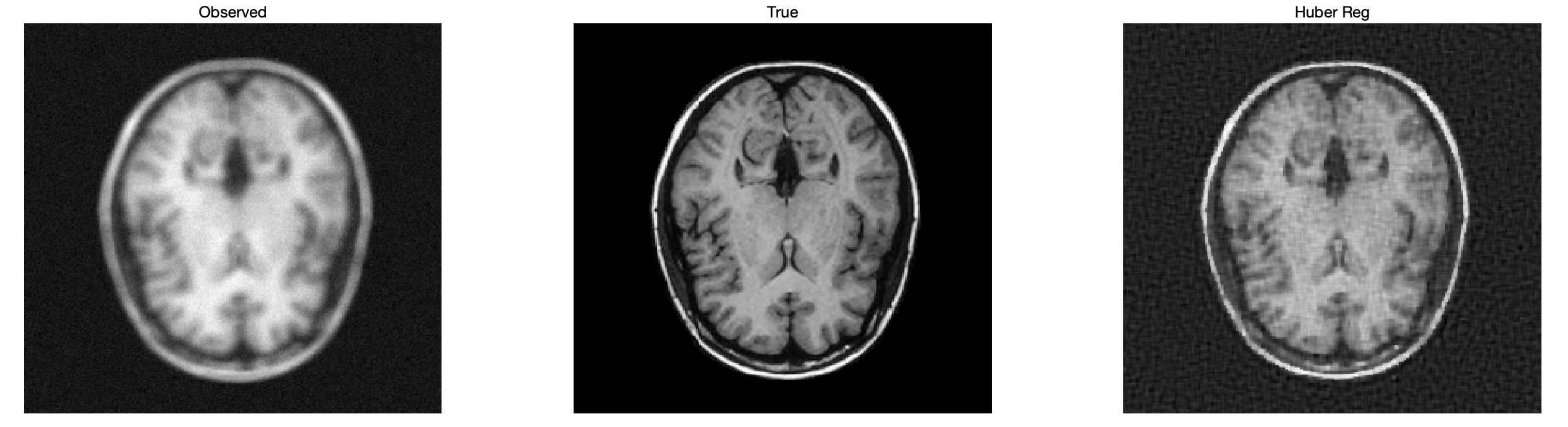
%% 计算各结果的MSE和PSNR 并对比
load('x_first_method.mat','x_first_method');
load('x_posterior_mean.mat','x_posterior_mean');
% 计算各结果的MSE和PSNR
mse_observed = mean((TrueImage(:) - ObservedImage(:)).^2);
mse_wiener = mean((TrueImage(:) - x_first_method(:)).^2);
mse_posterior = mean((TrueImage(:) - x_posterior_mean(:)).^2);
mse_huber = mean((TrueImage(:) - x(:)).^2);
psnr_observed = 10*log10(max(TrueImage(:))^2 / mse_observed);
psnr_wiener = 10*log10(max(TrueImage(:))^2 / mse_wiener);
psnr_posterior = 10*log10(max(TrueImage(:))^2 / mse_posterior);
psnr_huber = 10*log10(max(TrueImage(:))^2 / mse_huber);
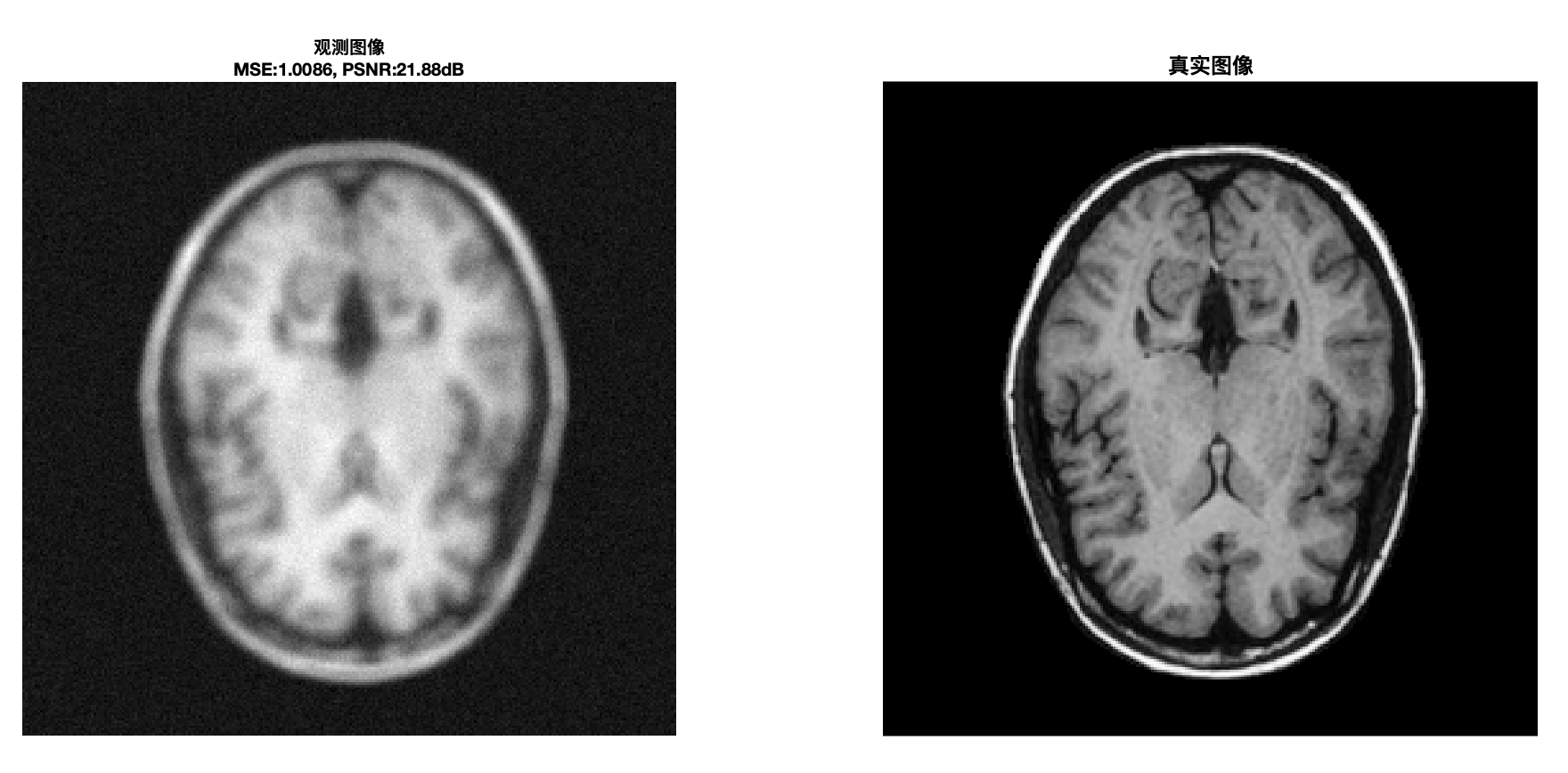
figure('Name','最终对比展示','NumberTitle','off','Color','w');
subplot(1,2,1);
imagesc(ObservedImage); colormap gray; axis image off;
title({['观测图像'], ...
['MSE:' num2str(mse_observed,'%.4f') ', PSNR:' num2str(psnr_observed,'%.2f') 'dB']},...
'FontWeight','bold','FontSize',10);
subplot(1,2,2);
imagesc(TrueImage); colormap gray; axis image off;
title('真实图像','FontWeight','bold','FontSize',12);
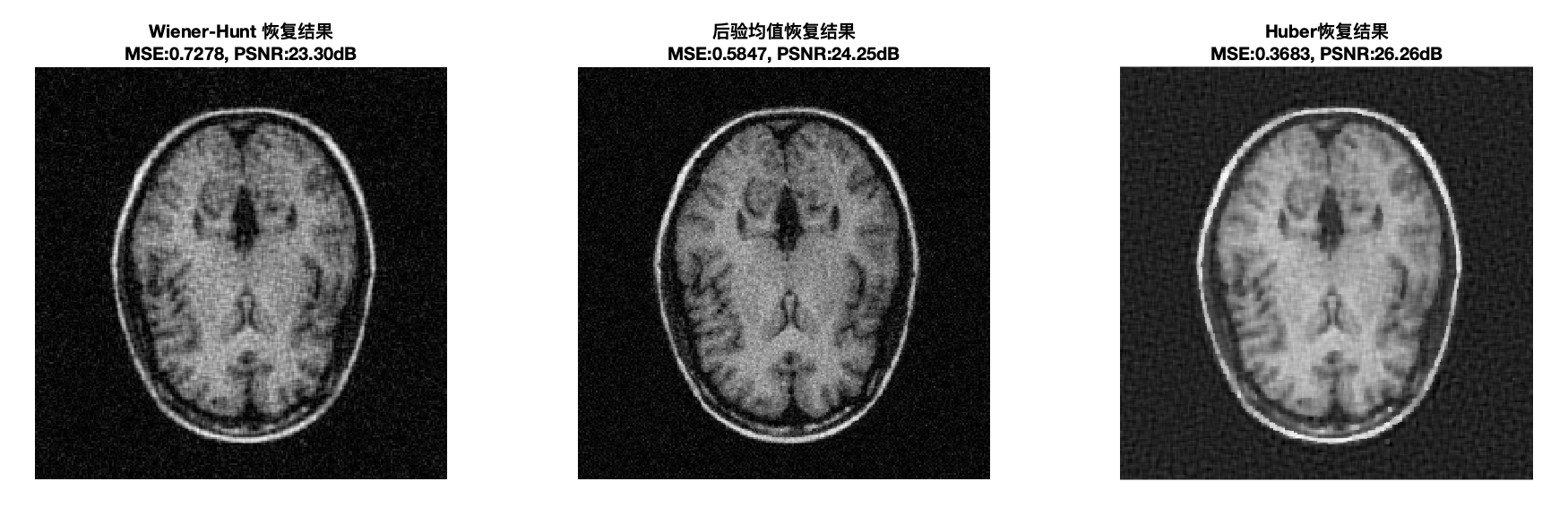
figure('Name','最终对比展示','NumberTitle','off','Color','w');
subplot(1,3,1);
imagesc(abs(x_first_method)); colormap gray; axis image off;
title({['Wiener-Hunt 恢复结果'], ...
['MSE:' num2str(mse_wiener,'%.4f') ', PSNR:' num2str(psnr_wiener,'%.2f') 'dB']},...
'FontWeight','bold','FontSize',10);
subplot(1,3,2);
imagesc(abs(x_posterior_mean)); colormap gray; axis image off;
title({['后验均值恢复结果'], ...
['MSE:' num2str(mse_posterior,'%.4f') ', PSNR:' num2str(psnr_posterior,'%.2f') 'dB']},...
'FontWeight','bold','FontSize',10);
subplot(1,3,3);
imagesc(x); colormap gray; axis image off;
title({['Huber恢复结果'], ...
['MSE:' num2str(mse_huber,'%.4f') ', PSNR:' num2str(psnr_huber,'%.2f') 'dB']},...
'FontWeight','bold','FontSize',10);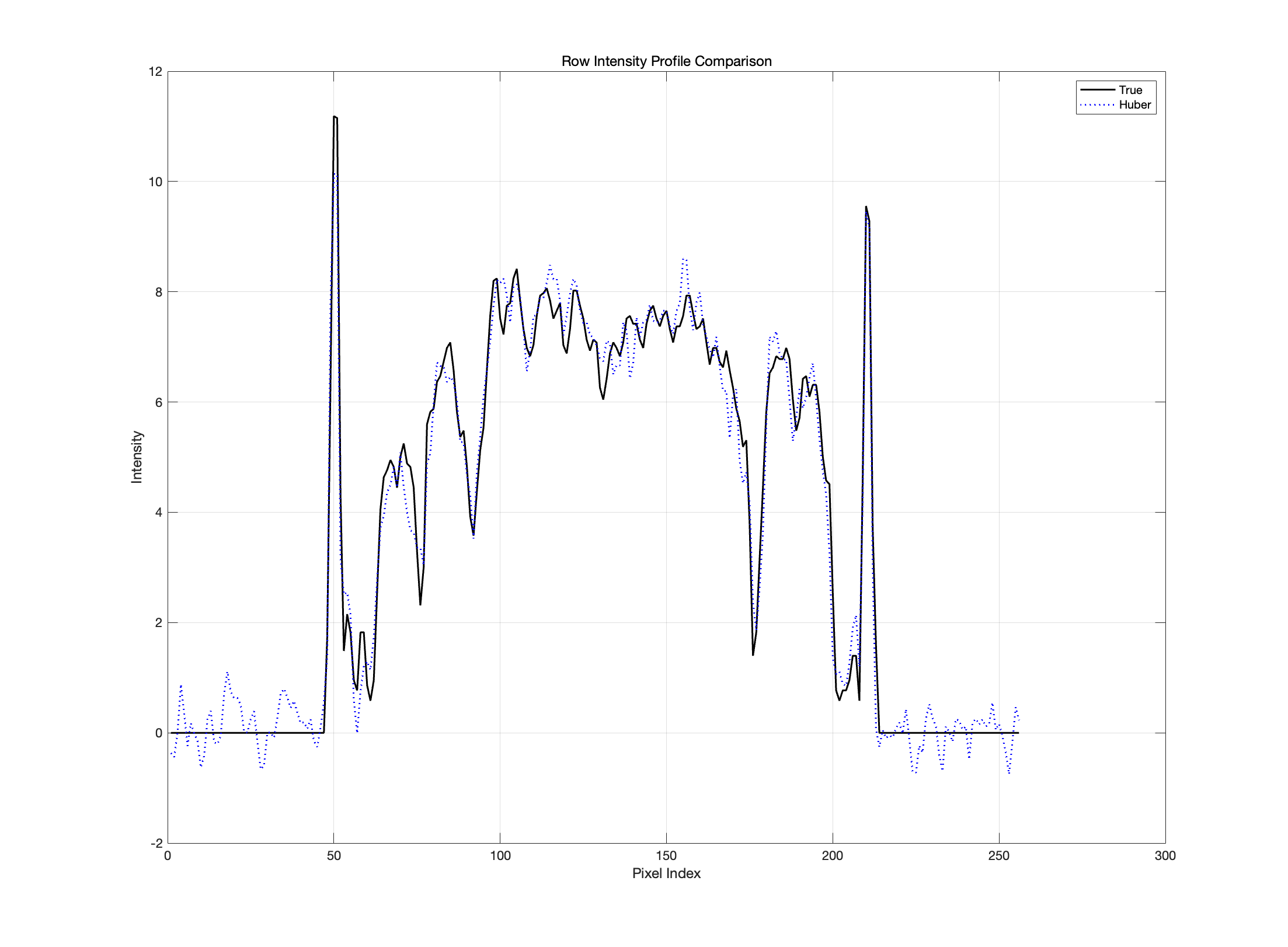
进一步分析: 使用线变量的解释
我们对之前的理论进行新解释(不是新方案)。这是对准则 (3) 及其最小化解 的另一种解释。它利用了线变量,可以揭示重建图像中的不连续性。为此,我们再次引入一个全新的扩展准则 (5) :
线变量 \ell _{pq} \in [0,1] 是未观测到的,它们被引入到相邻像素之间,以打破或削弱像素间的相互作用
对比准则 (1)
对比准则 (3)
对比准则 (4)
这个形式重点在于线变量\ell _{pq},在正则化项\mu \sum _{p \sim q} \ell _{pq}(x _p - x _q)^2 中\ell _{pq}可以调节像素相互作用强度 ,也就是每对相邻像素 p 和 q 之间的平滑程度。
当\ell_{pq} 较大时, 表示对(x_p - x_q)^2 的惩罚较强,即倾向于平滑作用强,图像噪声少,细节少。尤其是当\ell_{pq} = 1 ,任何像素之间的差异都会被平滑,图像完全丢失细节
当\ell_{pq} 较小时, 表示对(x_p - x_q)^2 的惩罚较弱,倾向于保留边缘细节。尤其是当\ell_{pq}=0 ,完全没有平滑作用,图像会充满噪声。
这个 作用和\alpha 差不多,但是最重要的是后面的\sum_{p \sim q} \bar{\zeta}(\ell_{pq}) ,它是一个对线变量\ell_{pq} 的正则化项,用于控制调节\ell_{pq} 的取值范围,其函数形式给出:
\bar{\zeta} 函数可以通过凸对偶框架构造出来。直接给出的结果如下:
其中,$s = T$ 是Huber函数的阈值参数
证明
我们需要从扩展准则和凸对偶性的角度出发,利用 Legendre-Fenchel Transform 理论来推导出 \bar{\zeta}(\ell) 的表达式。
扩展准则 (5) :
考虑每对相邻像素 (p, q),我们假设势函数公式为:
其中,$\delta = x_p - x_q$ 是像素间的灰度差异
对比准则 (2)
可见,将势函数带进入,就可以得到准则 (5) ,我们继续对势函数动手:
我们调一下位置,可得:
根据勒让德-芬切尔变换的定义,对于凸函数f(\delta),其凸对偶函数f^ *(\ell) 定义为:
从这里我们就可以明白,为什么势函数的形式如上了,它是随着 勒让德-芬切尔变换 公式而构造来的。下面我们继续计算\bar{\zeta}(\ell)
根据Huber势函数的定义:
我们将其带入到\bar{\zeta}(\ell) = \sup_{\delta} \left[ \varphi_H(\delta) - \ell \delta^2 \right] 当中,要分情况讨论
情况 1: |\delta| \leq T
因此,
情况 2: |\delta| > T
因此,
为了找到最大值,我们对\delta > T 和\delta < -T 分别进行分析。
子情况 2.1: \delta > T
设\delta > T,则:
对 \delta 求导并设为零以找到极值点:
验证\delta^* > T 是否成立:
这在\ell \in [0,1) 时成立。
将\delta^* = \frac{T}{\ell} 代入表达式:
子情况 2.2: \delta < -T
由于对称性,结果与子情况 2.1 相同:
通过类似的步骤可得:
综上情况所述:
情况 1: \bar{\zeta}(\ell) = (1 - \ell) T^2
情况 2: \bar{\zeta}(\ell) = T^2 \left( \frac{1}{\ell} - 1 \right)
为了确定\bar{\zeta}(\ell),我们取这两者中的最大值:
观察到,对于\ell \in (0,1):
因为:
因此,
如果我们设定 s = T,则:
证明完毕
这一结果表明, \bar{\zeta}(\ell) 是通过凸对偶性和勒让德-芬切尔变换从原始的Huber正则化函数导出的,它有效地将线变量\ell 与正则化项关联起来。
如果没有 \bar{\zeta} ,优化过程会自由的选择\ell_{pq} 值,而不注重于像素差异,这会导致极端的\ell_{pq} 值(接近 0 或 1)。在后续算法步骤中会清楚这一点。
我们下面会推导这个新准则 (5) 和初始准则 (1) 的关系。
首先,我们需要再引入一个关于\ell 的函数,记作\psi_\delta(\ell),其参数为\delta:
通过最小化\psi_\delta(\ell) 关于\ell,我们可以得到\varphi_H(\delta),即:
接下来我们给出证明
证明
回顾定义\zeta(\ell) 和\psi_\delta(\ell):
求\psi_\delta(\ell) 关于\ell 的导数并令其为零:
考虑\ell^* 的取值范围:
当|\delta| \leq s 时:
当|\delta| > s 时:
综合起来:
将\ell^* 代回去计算最小值\varphi_H(\delta):
当|\delta| \leq s:
当|\delta| > s:
对比初始Huber 势函数表达式
一摸一样啊,因此,证明了:
下面我们会证明,准则 (5) 如何通过最小化最小化辅助变量\ell 来得到准则 (2) ,即:
证明
首先,回顾两个准则的定义:
初始准则(2):
扩展准则 (5):
步骤:
固定x,对\bar{J}_H(x, \ell) 关于\ell 进行最小化:
① 对于给定的x, \bar{J}_H(x, \ell) 关于\ell 的部分可以拆分为像素对(p, q) 的独立项:
因此,我们可以分别最小化每个像素对(p, q) 的项:
②对\psi_{pq}(\ell_{pq}) 关于\ell_{pq} 求最小值:
求导并令导数为零:
解方程得到最优\ell_{pq}:
③利用\zeta(\ell) 的具体形式求解\ell_{pq}:
已知辅助函数\zeta(\ell) 定义为:
因此,其导数为:
将其代入前的等式:
整理得到:
因为\ell_{pq} > 0,所以:
需要注意\ell_{pq} \leq 1,因此当|x_p - x_q| \leq s 时, \ell_{pq} \geq 1,但由于\ell_{pq} \leq 1,所以取\ell_{pq} = 1。
最终,最优\ell_{pq} 为:
④ 将最优\ell_{pq}^ * 代入\psi_{pq}(\ell_{pq}^) 计算最小值:
当|x_p - x_q| \leq s 时:
当|x_p - x_q| > s 时:
结合起来:
可见,最小化后的\psi_{pq}(\ell_{pq}^*) 即为 Huber 势函数\varphi_H(x_p - x_q),回顾 Huber 势函数定义:
可见两个表达式一摸一样,我们可以说:
⑤ 将结果代入扩展准则,得到初始准则:
这就是初始准则J_H(x) 的形式,因此我们可以说,通过对准则 (5)\bar{J}_H(x, \ell) 关于\ell 进行最小化,我们得到了:
证明完毕
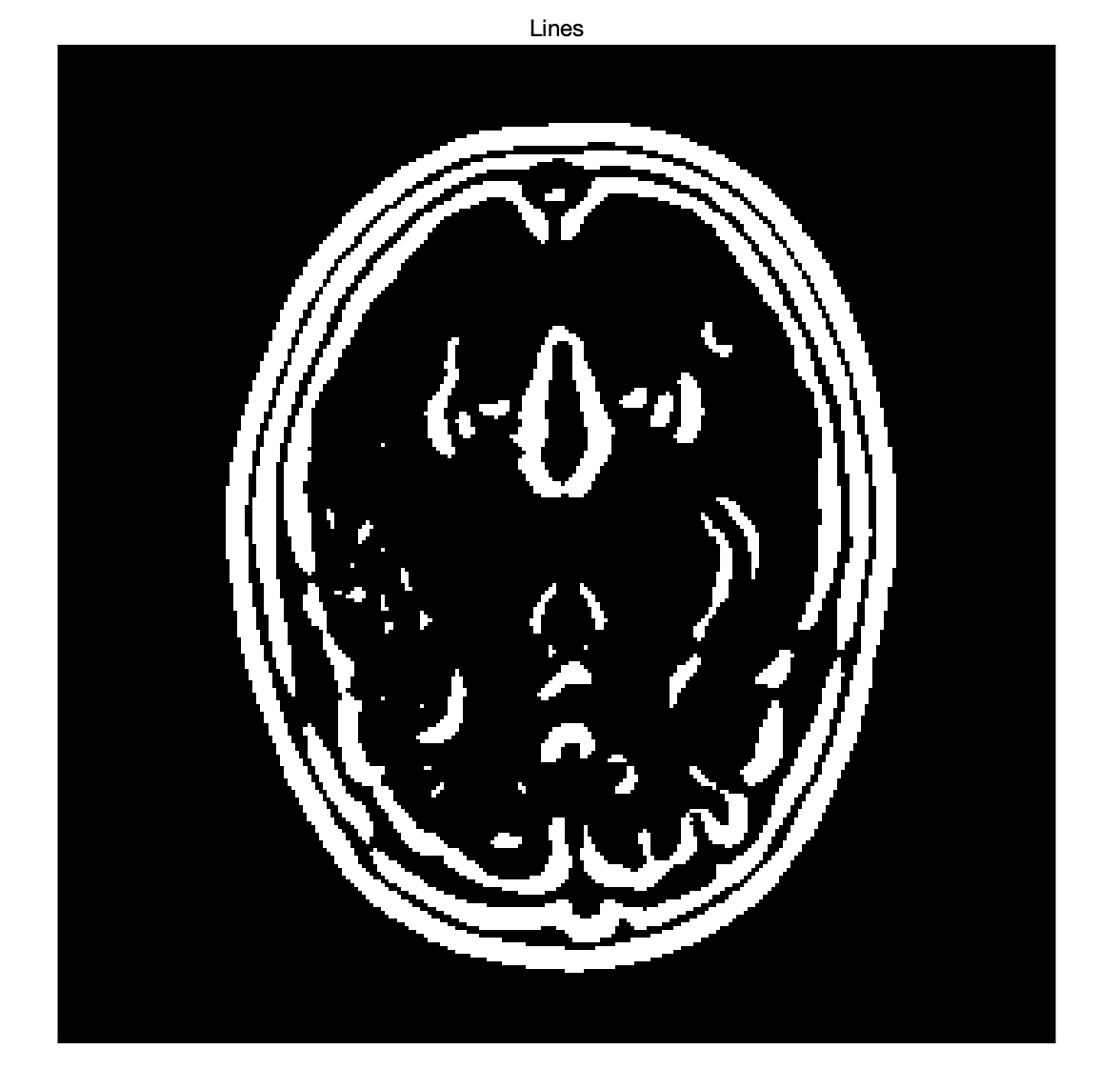
接下来我们 绘制与解\hat{x}_H 对应的线条 ,线条 ( \hat{\ell} ) 可以直观地看作是图像的边缘检测结果。通过对\ell 进行最小化,在恢复图像的过程中可以识别并标记图像中的边缘位置。
步骤:
① 计算梯度: 计算图像\hat{x} _H 的梯度\delta _{pq} = x _p - x _q,用于评估相邻像素间的差异。
② 线条的表示: 根据辅助变量\ell _{pq},通过以下公式计算每对相邻像素之间的相互作用:
较小的\ell _{pq} 表示强烈的不连续性(即图像边缘)。
③ 生成线条图像: 将计算出的\hat{\ell} 映射到新的图像矩阵中。生成的图像可以是一个二值图像(黑白)或灰度图像,用以突出显示恢复图像中的边缘。
% ----------------------------
% Step 10: 使用 ImageRestoration 并绘制线条图像
% ----------------------------
mu = 1;
T_for_lines = 1;
[N_inline, M_inline] = size(ObservedImage);
IR_padded_inline = MyFFT2RI(IR, N_inline);
Dx_inline = [0, 0, 0; 0, -1, 1; 0, 0, 0];
Dy_inline = [0, 0, 0; 0, -1, 0; 0, 1, 0];
F_Dx_inline = MyFFT2RI(Dx_inline, N_inline);
F_Dy_inline = MyFFT2RI(Dy_inline, N_inline);
Reg_term_inline = abs(F_Dx_inline).^2 + abs(F_Dy_inline).^2;
x_inline = ObservedImage;
a_inline = zeros(N_inline, M_inline, 2);
for k_inline = 1:max_iter
F_Data_inline = MyFFT2(ObservedImage);
Reg_a_x_inline = MyFFT2(a_inline(:,:,1)) .* F_Dx_inline + MyFFT2(a_inline(:,:,2)) .* F_Dy_inline;
Cov_x_inline = 1 ./ (abs(IR_padded_inline).^2 + mu * Reg_term_inline);
Mean_x_inline = Cov_x_inline .* (conj(IR_padded_inline) .* F_Data_inline + mu * Reg_a_x_inline);
x_inline = real(MyIFFT2(Mean_x_inline));
delta_x_h_inline = x_inline(:, [2:end, end]) - x_inline;
delta_x_v_inline = x_inline([2:end, end], :) - x_inline;
a_h_inline = delta_x_h_inline;
a_v_inline = delta_x_v_inline;
idx_h_large_inline = abs(delta_x_h_inline) > T_for_lines;
idx_h_small_inline = abs(delta_x_h_inline) <= T_for_lines;
a_h_inline(idx_h_large_inline) = delta_x_h_inline(idx_h_large_inline) - 2*alpha * T_for_lines .* sign(delta_x_h_inline(idx_h_large_inline));
a_h_inline(idx_h_small_inline) = (1 - 2 * alpha) * delta_x_h_inline(idx_h_small_inline);
idx_v_large_inline = abs(delta_x_v_inline) > T_for_lines;
idx_v_small_inline = abs(delta_x_v_inline) <= T_for_lines;
a_v_inline(idx_v_large_inline) = delta_x_v_inline(idx_v_large_inline) - 2*alpha * T_for_lines .* sign(delta_x_v_inline(idx_v_large_inline));
a_v_inline(idx_v_small_inline) = (1 - 2 * alpha) * delta_x_v_inline(idx_v_small_inline);
a_inline(:,:,1) = a_h_inline;
a_inline(:,:,2) = a_v_inline;
end
restored_image = x_inline;
% ----------------------------
% Step 11: 绘制边缘检测结果
% ----------------------------
% 调用自定义的 plot_edges 函数
threshold = 0.5;
plot_edges(restored_image, threshold);function plot_edges(restored_image, threshold)
% 计算水平与垂直方向梯度差分
delta_x_h = restored_image(:, [2:end, end]) - restored_image; % Horizontal differences
delta_x_v = restored_image([2:end, end], :) - restored_image; % Vertical differences
% 计算梯度幅度
gradient_magnitude = sqrt(delta_x_h.^2 + delta_x_v.^2);
% 根据阈值生成二值图
lines = gradient_magnitude > threshold;
% 显示二值图像,0为黑色,1为白色
figure;
imshow(lines);
title('Lines');
end