最优滤波在AR模型与Singer轨迹目标跟踪中的应用
编辑任务目标
本节主要关注自回归(AR)过程的生成,首先我们从从极点出发生成广义平稳的自回归过程(二阶),然后展示其自回归信号的时域波形和功率谱图,验证其在时域上是否是广义平稳的,在频域上是否和极点特性一致。
随后我们将生成的自回归信号作为输入,分别用 NLMS 和卡尔曼滤波器自适应算法来在线估计自回归系数a_1, a_2 以及噪声方差,同时比较不同算法的收敛速度和精度,并进行分析
广义平稳的 自回归过程(AR过程) 是一种常见的随机过程模型,在时间序列分析中有广泛的应用。既然要生成广义平稳的 AR 过程,我们先补充广义平稳和AR过程的定义。
广义平稳的定义
满足下列两条即可称为广义平稳:
均值平稳: 对任意时间t,都有
\mathbb{E}[X_t] = \mu其中\mu 为常数,不随t 改变。
协方差平稳: 对任意时间t_1、 t_2,它们的协方差只依赖于时间间隔\tau = |t_1 - t_2|,即
\mathrm{Cov}\bigl(X_{t_1}, X_{t_2}\bigr) = \gamma(\tau)
即 若时序的均值不随时间改变,且自相关结构只依赖于时间滞后,我们就称它是广义平稳序列。广义平稳只关注一阶与二阶矩,而严格平稳的要求更高,如果若\{X_t\} 服从多元正态分布,则期望和协方差可完全描述其统计特性。此时 广义平稳 与 严格平稳 等价。
自回归过程(AR Process)
定义
在时间序列分析中,一个p 阶自回归过程定义为:
简化写为:
自回归过程假设x(k) 与其前p 个时刻的值呈线性关系,换句话说,根据过去值预测未来值。每个过去值都有一个权重\{a_i\} ,在自回归过程中我们要做的任务就是估计这个参数,常见的估计方法有三种: 最小二乘(OLS) Yule-Walker 方程 最大似然(ML) 或带先验的贝叶斯估计 ,这里不做详细介绍。
在本内容中,为了生成一个这样的自回归过程,我们需要直接给出\{a_i\} 和u(k) 对应的高斯白噪音方差。在后续工作中,我们会利用不同的方法来重新估计这个AR过程的参数。但是\{a_i\} 的给出是有讲究的,不是直接取值就完了,我们要从传递函数极点入手。
从极点到 AR 系数
在z 域中,AR(p) 模型对应的特征多项式可写为
过程如下:
一个p 阶自回归过程定义:
可将其重写为
在Z域中对应关系:
那么AR模型的特征多项式(即分母多项式)为:
在z 域中,AR(p) 模型对应的传递函数可写为:
则有
可以看出,多项式系数\{a_i\} 与极点\{p_i\} 是对应的。
AR 过程生成实现代码
因此,我们输入传递函数极点p 以及高斯白噪音u 的方差,我们可以生成一个AR 过程,下面给出 AR 过程的matlab生成函数如下。
function signal = AR_generation(poles, variance, numSamples)
输入为极点向量
poles、噪声方差variance、以及信号长度numSamples。输出则是模拟生成的 AR 信号signal。
当我们拿到方差和信号长度的时候,我们已经可以把高斯白噪音构建出来,即
whiteNoise = sqrt(variance) * randn(numSamples, 1);
randn(numSamples, 1) 会生成 X \sim N(0,1) ,我们再将其乘以 sqrt(variance) ,那么 Y = sqrt(variance)*X的分布为Y \sim N(0,variance) ,至此,我们生成了一个均值为0、方差为variance的高斯白噪声序列u(k)。
接下来我们利用极点p_1, p_2, \cdots, p_p 来生成 AR 过程,重新回顾上面得到的对应方程
使用 poly(poles) 会返回系数向量a_i,对应的matlab实现为:
ar_coeffs = poly(poles);
在我们的代码中,我们使用的是二阶AR模型,因此AR 模型的多项式为:
如果极点为p_1, p_2,则特征多项式可因式分解为:
比较后可得:
至此我们得到了对应特征方程的系数a_i ,接下来我们要用这些参数生成信号
signal = filter(1, ar_coeffs, whiteNoise);
给定输入信号
x,通过分子系数为b、分母系数为a的线性时不变系统滤波器后,输出y。
因为AR过程定义就是x(k) 在z 域下相对于u(k) 的传递函数为1/A(z),因此为了反向得到x(k) ,只需要将u(k) 经过1/A(z)这个滤波器即可。具体实现过程需要到 filter函数中去看。因此我们得到了满足该AR模型定义的时域信号序列x(k) 叫做 signal。
时域图和功率谱图
接下来我们绘制它的时间序列和功率谱
% 4. 绘制 AR 过程的时间序列
figure;
subplot(2,1,1)
plot(signal, 'b');
title('AR 过程的时间序列');
xlabel('样本编号');
ylabel('幅度');
grid on;
% 计算并绘制功率谱
subplot(2,1,2)
[Pxx, f] = periodogram(signal, [], [], 1);
plot(f, 10*log10(Pxx), 'g');
title('AR 过程的功率谱密度(周期图)');
xlabel('频率 (Hz)');
ylabel('功率谱密度 (dB/Hz)');
grid on;
搞定了 AR_generation自回归生成函数,我们就需要在主函数中定义必要参数来调用它了。也就是需要提前定义信号长度 numSamples、噪声方差 variance、以及极点向量 poles(同时绘制单位圆和极点的位置,来判断其稳定性)。
numSamples = 5000; % 样本数量
variance = 1; % 白噪声方差
poles = [0.7 + 0.5i, 0.7 - 0.5i]; % 共轭复数极点,为确保稳定性,极点必须位于单位圆内
然后调用
signal = AR_generation(poles, variance, numSamples);
利用 NLMS 和卡尔曼滤波器 对生成的 AR 信号进行参数估计
我们要把刚刚生成 的 AR 自回归信号作为输入,然后利用NLMS 滤波器和卡尔曼滤波两种方法来估计它的参数和高斯白噪音的方差,然后和真实 AR 参数做对比,真实 AR 参数我们之前已经计算过,我们重新提取一次得到a_1, a_2
ar_coeffs = poly(poles); % 返回 [1, -a1, -a2]
true_ar_params = -ar_coeffs(2:end)';
还需要设置 模型阶数 和 过渡期(transient):
order = 2
transient = 0; % 舍弃的样本数量
若在实际应用中,滤波器在初始阶段估计不稳定,通常会丢弃 (舍弃) 这部分样本,不丢弃也可以。
NLMS算法
输入向量的构建,我们将过去p 个样本组织成一个输入向量
其代码实现为
x_history = zeros(order, numSamples); % 变量初始化
x_buf = signal(n-1:-1:n-order); %选取对应信号
x_history(:, n) = x_buf; %保存
我们的目的是为了估计AR模型系数a_1(k),\;a_2(k),\;\dots,\;a_p(k) ,可以把它们排成一个列向量:
这种向量化处理使得参数估计可视为寻找一个向量\underline{\mathbf{H}}_N(k) = [a_1(k), \dots, a_p(k)]^T,使得\underline{\mathbf{H}}_N(k) 与\underline{\mathbf{X}}_N(k) 的内积能够逼近x(k)。
滤波器输出的计算
在自适应滤波器中,上一时刻的参数向量\underline{\mathbf{H}}_N(k-1) 与当前的输入向量\underline{\mathbf{X}}_N(k) 做内积(点乘),即可得到当前时刻的预测输出y(k)
可以理解为样本通过参数加权求和,得出当前预测输出。
y_nlms(n) = h' * x_buf;
误差的计算
为了评估参数的好坏,将实际观测的输出d(k)=x(k) 与预测输出y(k) 比较,定义误差为:
e_nlms(n) = d - y_nlms(n);
更新滤波器系数:
最小均方误差(MSE)准则表明,为了减小误差,我们需要沿着负梯度方向更新参数,这就是 LMS(Least Mean Square)算法的思想。然而,当输入信号幅度变化很大时,LMS 的步长难以合理选择。为克服这一问题,引入归一化处理得到 NLMS(Normalized LMS):
\beta 的作用是防止分母为0。
h = h + (mu / (beta + pi_x)) * x_buf * e_nlms(n);
% 存储系数历史
h_history_nlms(:, n) = h;
在实际实现中常用平滑指标 pi_x 来估计输入功率:
pi_x = gamma * pi_x + (1 - gamma) * norm_x;
其中:
norm_x = norm_x + x_buf(1)^2 - x_history(end, n-1)^2;
其中注意,初始化的时候不能这么写,对应代码为:
pi_x = norm_x;
norm_x = sum(x_buf.^2);
然后循环结束,得到滤波器系数h,重命名叫做 estimated_ar_params_nlms。
最后估计噪声方差 estimated_variance_nlms
estimated_variance_nlms = var(e_nlms(transient+1:end));
卡尔曼滤波框架
状态空间模型描述:
若将 AR 参数视为状态随时间缓慢变化的动态系统,则可使用卡尔曼滤波(Kalman Filter)来对其进行最优估计。重申估计目标是自回归模型的参数向量。
输入向量为过去的样本:
输出为当前样本:
状态方程:
测量方程:
H(k) 矩阵就是\mathbf{y}_{\text{past}} 也就是x
u(k) 和 v(k)分别为过程噪声和测量噪声, \mathbf{v}(k) \sim \mathcal{N}(\mathbf{0},\mathbf{Q})v(k) \sim \mathcal{N}(0,R) ,并且有协方差定义:
我们要对自回归模型估计参数向量。此时,将AR参数向量定义为状态向量:
假设参数随时间缓慢变化,可用单位矩阵来定义参数状态随时间的转移矩阵,即:
具体步骤
卡尔曼滤波分为 预测 (Time Update) 和 更新 (Measurement Update) 两部分。
预测步骤
先验状态估计:
先验协方差更新
在本代码中, \Phi = I,且 G(k)=I,因此:
a_hat_prior = a_hat(:, k-1);
P_prior = P + Q;
更新步骤:
给出观测y(k) 后,利用卡尔曼增益K(k) 修正先验估计:
a_hat(:, k) = a_hat_prior + K * (y - x' * a_hat_prior);
这里 x 对应于\mathbf{y}_{\text{past}} ,也就是对应H(k) 。
利用卡尔曼增益K(k) 修正后验协方差:
P = (eye(order) - K * x') * P_prior;
误差向量:
e_kalman(k) = y - x' * a_hat_prior;
最终,通过卡尔曼滤波迭代,a_hat(:, end)给出最后时刻的参数估计\hat{a}(k|k),即AR参数的后验估计。
最后可对e_\text{kalman} 计算方差:
estimated_variance_kalman = var(e_kalman(transient+1:end));
通过卡尔曼滤波过程,我们在每一步中动态平衡先验预测与先验观测信息的权重,从而获得比单纯LMS/NLMS更精确和快速收敛的参数估计。
下面给出完整的代码和子函数
clear all;
clc;
close all;
%% 第一步任务目标: 生成一个广义平稳的 AR 过程,为此我们必须事先定义其传递函数的极点和生成 AR 过程的方差。
%% 随后我们显示这个 AR 过程生成的信号,并且查看他的功率谱密度。 最后评论极点对其影响。
% 设置随机数种子以获得可重复的结果
rng(0);
% AR 信号生成参数
numSamples = 5000; % 样本数量
variance = 1; % 白噪声方差
% 定义 AR(2) 模型的极点
poles = [0.7 + 0.5i, 0.7 - 0.5i];
% 绘制极点在复平面的位置
figure;
theta = linspace(0, 2*pi, 100);
plot(cos(theta), sin(theta), 'r--', 'DisplayName', '单位圆');
hold on;
plot(real(poles), imag(poles), 'bo', 'DisplayName', 'AR 模型极点');
axis equal;
xlabel('实部');
ylabel('虚部');
title('AR 模型极点在复平面中的位置');
legend show;
grid on;
% 生成 AR(2) 信号
signal = AR_generation(poles, variance, numSamples);
%% 第二步任务目标: 估计 AR 参数和生成过程的方差
%% 我们输入一个自回归信号,然后使用NLMS 滤波器和卡尔曼滤波两种方法来估计 这个自回归信号的参数和高斯白噪声的方差
% 真实的 AR参数 (根据极点计算)
ar_coeffs = poly(poles); % 返回 [1, -a1, -a2]
true_ar_params = -ar_coeffs(2:end)';
% 公共参数
order = 2; % AR 模型阶数
transient = 500; % 舍弃的样本数量
% =================== NLMS 算法 ===================
% NLMS 算法参数
mu = 0.01;; % 步长参数(0 < mu < 2)
beta = 1e-6; % 正则化参数,防止除以零
gamma = 1 - 1/order; % 衰减因子
% 初始化
h = zeros(order, 1); % 滤波器系数
e_nlms = zeros(numSamples, 1); % 误差向量
y_nlms = zeros(numSamples, 1); % 滤波器输出
norm_x = 0; % 输入向量的范数平方
pi_x = 0; % 输入信号功率的估计
h_history_nlms = zeros(order, numSamples); % 系数历史记录
x_history = zeros(order, numSamples); % 输入信号历史
% NLMS 算法迭代
for n = order+1:numSamples
% 输入向量(过去的样本)
x_buf = signal(n-1:-1:n-order);
x_history(:, n) = x_buf;
% 滤波器输出
y_nlms(n) = h' * x_buf;
% 期望输出
d = signal(n);
% 计算误差
e_nlms(n) = d - y_nlms(n);
% 递归更新输入向量的范数平方
if n == order+1
% 初始化 norm_x
norm_x = sum(x_buf.^2);
else
% 更新 norm_x
norm_x = norm_x + x_buf(1)^2 - x_history(end, n-1)^2;
end
% 递归估计输入信号功率 pi_x
if n == order+1
pi_x = norm_x;
else
pi_x = gamma * pi_x + (1 - gamma) * norm_x;
end
% 更新滤波器系数
h = h + (mu / (beta + pi_x)) * x_buf * e_nlms(n);
% 存储系数历史
h_history_nlms(:, n) = h;
end
% 估计的 AR 参数(使用 NLMS)
estimated_ar_params_nlms = h;
% 估计噪声方差(使用 NLMS)
estimated_variance_nlms = var(e_nlms(transient+1:end));
% =================== 卡尔曼滤波器算法 ===================
% 初始化参数估计
a_hat = zeros(order, numSamples); % 参数估计
P = 1000 * eye(order); % 误差协方差矩阵初始化
% 过程噪声协方差矩阵 Q
Q = 1e-5 * eye(order);
% 观测噪声方差 R
R = variance;
% 卡尔曼滤波器误差向量
e_kalman = zeros(numSamples,1);
% 卡尔曼滤波器迭代
for k = order+1:numSamples
% 观测值
y = signal(k);
% 输入向量(过去的样本)
x = signal(k-1:-1:k-order);
% 状态预测
a_hat_prior = a_hat(:, k-1);
% 误差协方差预测
P_prior = P + Q;
% 卡尔曼增益
K = P_prior * x / (x' * P_prior * x + R);
% 状态更新
a_hat(:, k) = a_hat_prior + K * (y - x' * a_hat_prior);
% 误差协方差更新
P = (eye(order) - K * x') * P_prior;
% 计算误差
e_kalman(k) = y - x' * a_hat_prior;
end
% 估计的 AR 参数(使用卡尔曼滤波器)
estimated_ar_params_kalman = a_hat(:, end);
% 估计噪声方差(使用卡尔曼滤波器)
estimated_variance_kalman = var(e_kalman(transient+1:end));
% =================== 结果显示 ===================
% 显示估计的 AR 参数
fprintf('真实的 AR 参数:\n');
for i = 1:order
fprintf('a%d = %.4f\n', i, true_ar_params(i));
end
fprintf('\n估计的 AR 参数(使用 NLMS):\n');
for i = 1:order
fprintf('a%d = %.4f\n', i, estimated_ar_params_nlms(i));
end
fprintf('\n估计的 AR 参数(使用卡尔曼滤波器):\n');
for i = 1:order
fprintf('a%d = %.4f\n', i, estimated_ar_params_kalman(i));
end
fprintf('\n真实的噪声方差: %.4f\n', variance);
fprintf('估计的噪声方差(NLMS): %.4f\n', estimated_variance_nlms);
fprintf('估计的噪声方差(卡尔曼滤波器): %.4f\n', estimated_variance_kalman);
% =================== 绘制结果 ===================
% 1. 滤波器系数收敛情况比较
figure;
subplot(2,1,1);
plot(h_history_nlms(1, :), 'b', 'DisplayName', 'NLMS a1');
hold on;
plot(a_hat(1, :), 'r', 'DisplayName', '卡尔曼滤波器 a1');
yline(true_ar_params(1), 'k--', '真实 a1');
title('滤波器系数 a1 收敛情况');
xlabel('样本编号');
ylabel('系数值');
legend;
grid on;
subplot(2,1,2);
plot(h_history_nlms(2, :), 'b', 'DisplayName', 'NLMS a2');
hold on;
plot(a_hat(2, :), 'r', 'DisplayName', '卡尔曼滤波器 a2');
yline(true_ar_params(2), 'k--', '真实 a2');
title('滤波器系数 a2 收敛情况');
xlabel('样本编号');
ylabel('系数值');
legend;
grid on;
% 2. 估计误差比较
figure;
subplot(2,1,1);
plot(e_nlms, 'b', 'DisplayName', 'NLMS 误差');
title('NLMS 估计误差 e(n)');
xlabel('样本编号');
ylabel('误差');
legend;
grid on;
xlim([1970 1995]); % 限制 x 轴范围
ylim([-10 10]); % 限制 y 轴范围
subplot(2,1,2);
plot(e_kalman, 'r', 'DisplayName', '卡尔曼滤波器 误差');
title('卡尔曼滤波器估计误差 e(n)');
xlabel('样本编号');
ylabel('误差');
legend;
grid on;
xlim([1970 1995]); % 限制 x 轴范围
ylim([-10 10]); % 限制 y 轴范围
% 3. 预测输出比较
figure;
% NLMS 输出
y_nlms_full = zeros(numSamples,1);
for n = order+1:numSamples
x_buf = signal(n-1:-1:n-order);
y_nlms_full(n) = h_history_nlms(:, n)' * x_buf;
end
% 卡尔曼滤波器输出
y_kalman = zeros(numSamples,1);
for k = order+1:numSamples
x = signal(k-1:-1:k-order);
y_kalman(k) = x' * a_hat(:, k-1);
end
plot(signal, 'k', 'DisplayName', '原始信号');
hold on;
plot(y_nlms_full, 'b--', 'DisplayName', 'NLMS 输出');
plot(y_kalman, 'r--', 'DisplayName', '卡尔曼滤波器输出');
title('原始信号与两种滤波器输出对比');
xlabel('样本编号');
ylabel('幅度');
legend;
grid on;
xlim([1970 1995]); % 限制 x 轴范围
ylim([-10 10]); % 限制 y 轴范围
function signal = AR_generation(poles, variance, numSamples)
% 生成一个广义平稳的 AR 过程
% 输入:
% poles - AR 模型的极点(向量)
% variance - 白噪声的方差
% numSamples - 样本数量
% 输出:
% signal - 生成的 AR 过程
% 1. 计算 AR 系数
% poly(poles) 返回 [1, a1, a2, ..., ap],对应特征方程的系数
ar_coeffs = poly(poles);
% 2. 生成白噪声序列
whiteNoise = sqrt(variance) * randn(numSamples, 1);
% 3. 通过滤波白噪声生成 AR 过程
% 滤波器的分母由 AR 系数组成
signal = filter(1, ar_coeffs, whiteNoise);
% 4. 绘制 AR 过程的时间序列
figure;
subplot(2,1,1)
plot(signal, 'b');
title('AR 过程的时间序列');
xlabel('样本编号');
ylabel('幅度');
grid on;
% 计算并绘制功率谱
% 计算并绘制周期图
subplot(2,1,2)
[Pxx, f] = periodogram(signal, [], [], 1);
plot(f, 10*log10(Pxx), 'g');
title('AR 过程的功率谱密度(周期图)');
xlabel('频率 (Hz)');
ylabel('功率谱密度 (dB/Hz)');
grid on;
end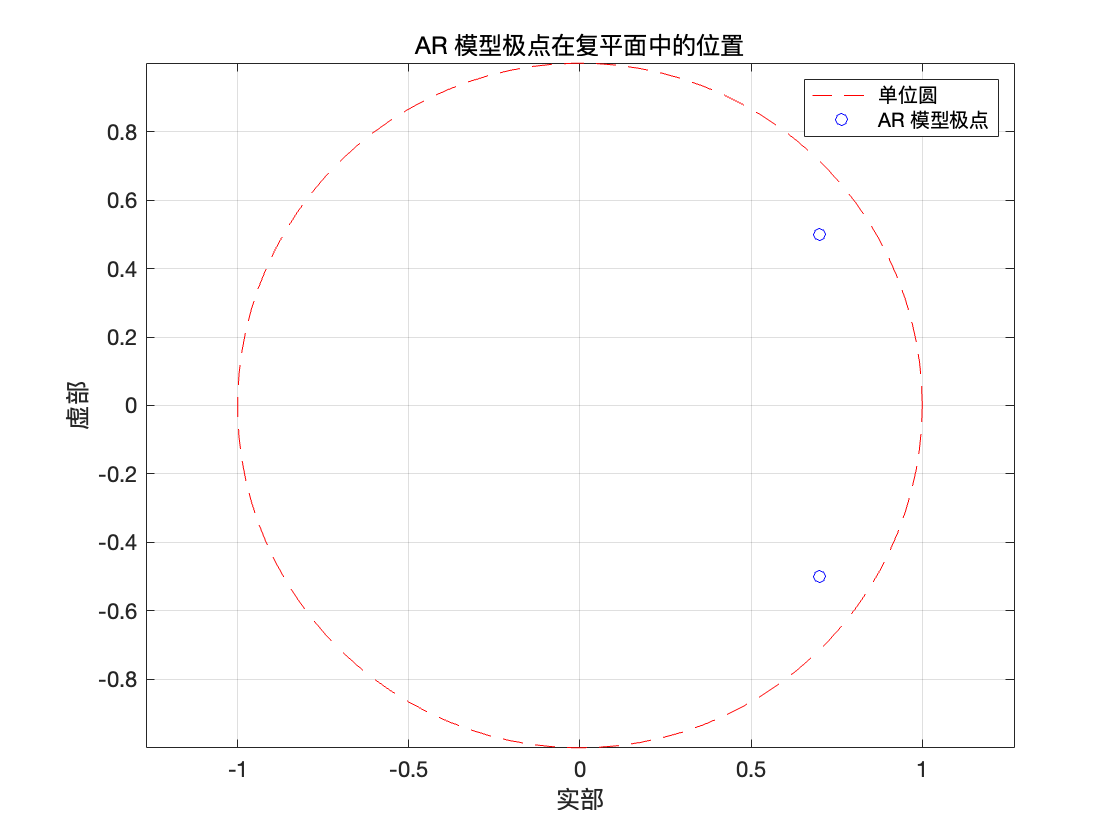
可见极点落在单位圆内,并且由于极点有非零虚部,说明该 AR 模型带有振荡成分(在功率谱上会有一个峰值,其频率对应极点的辐角),和功率谱结果是对应的。
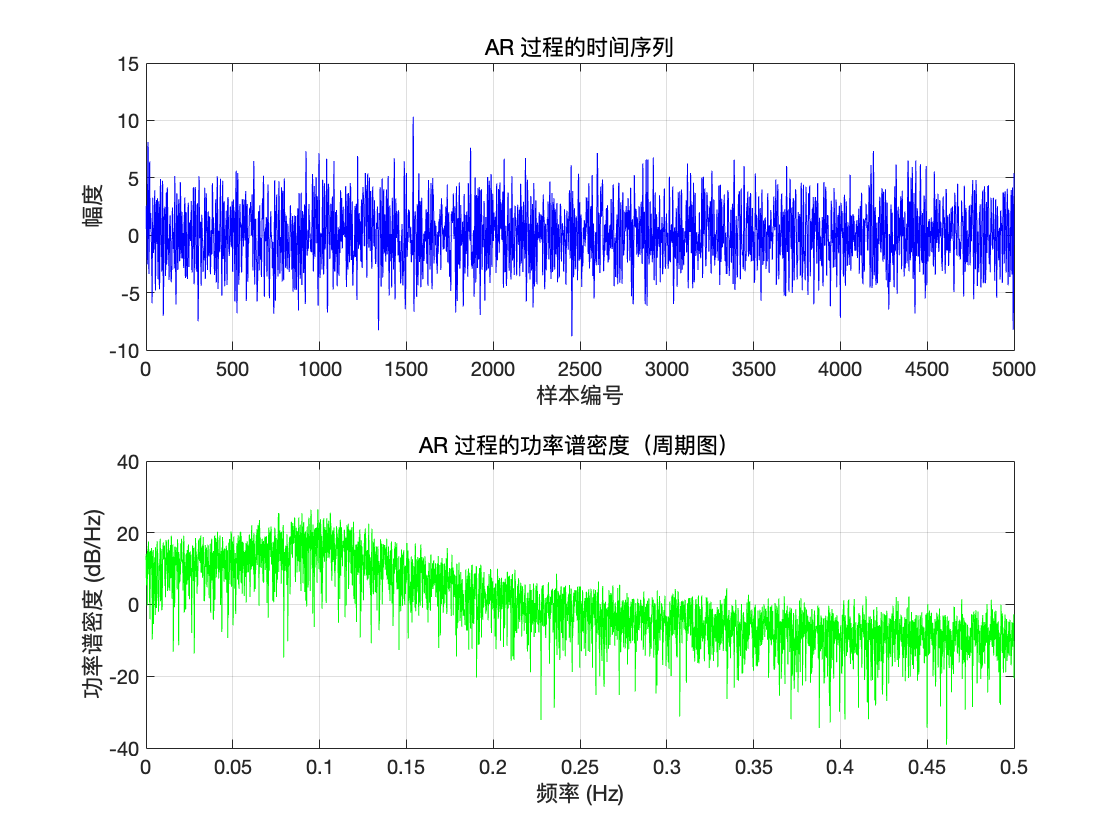
AR 过程的时间序列
信号在 5000 个采样点内 围绕 0上下随机波动,没有明显的趋势。符合广义平稳中的“均值平稳”,同时有稳定的方差。
AR 过程的功率谱密度
使用周期图(Periodogram)做了功率谱估计,并以对数(dB)方式呈现。 在某个频率段(约 0.1 Hz 附近)功率谱略有峰值,随后随频率升高而逐渐降低,这说明极点靠近单位圆,但是并不是极端能量峰值,所以可以判断离单位圆还有一定距离。
表1:AR 参数估计结果对比
表2:噪声方差估计结果对比
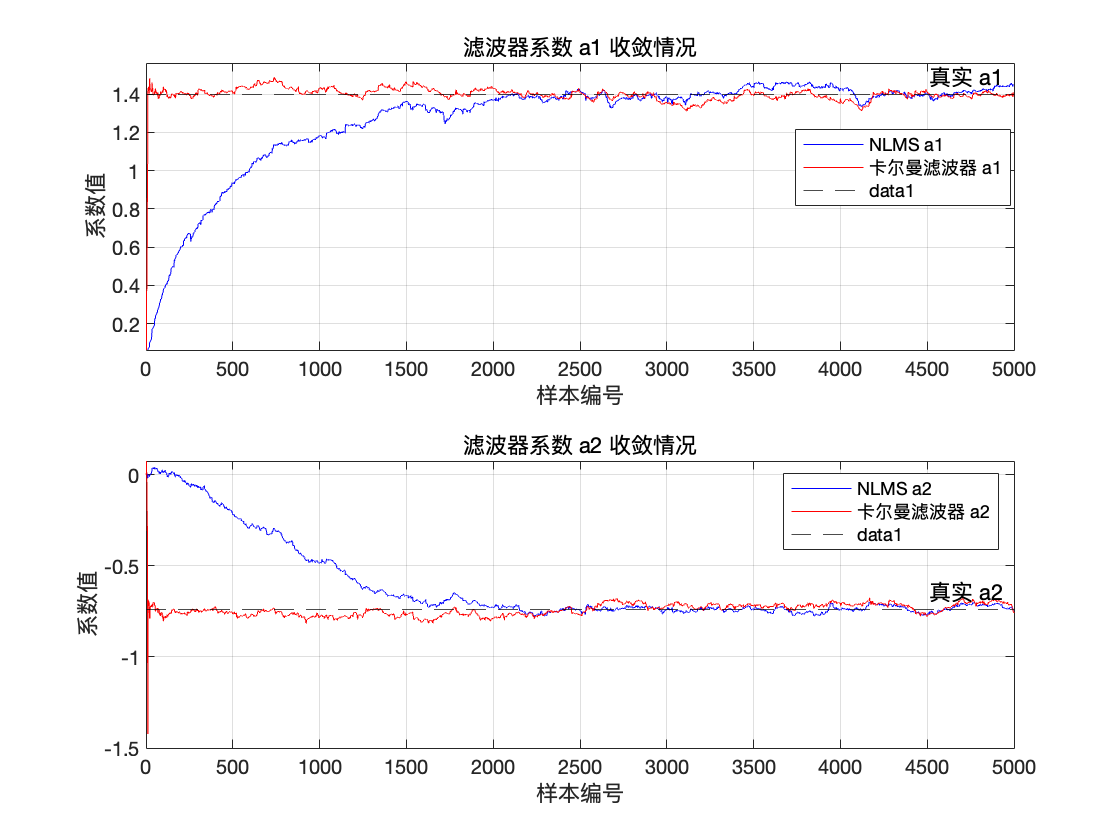
结果可见,对于NLMS,在初始时间内,有一个较明显的上升或下降过程,这是因为我们设置的步长较小,$\mu =0.01$ ,其收敛速度比较慢,但整个过程比较平滑,没有过大的波动。对于卡尔曼滤波,收敛速度非常快,短期迅速就可以逼近真实值。综合比较,卡尔曼滤波器的估计效果要远优于NLMS,但两种方法最后都能很好的收敛到真实自回归系数。
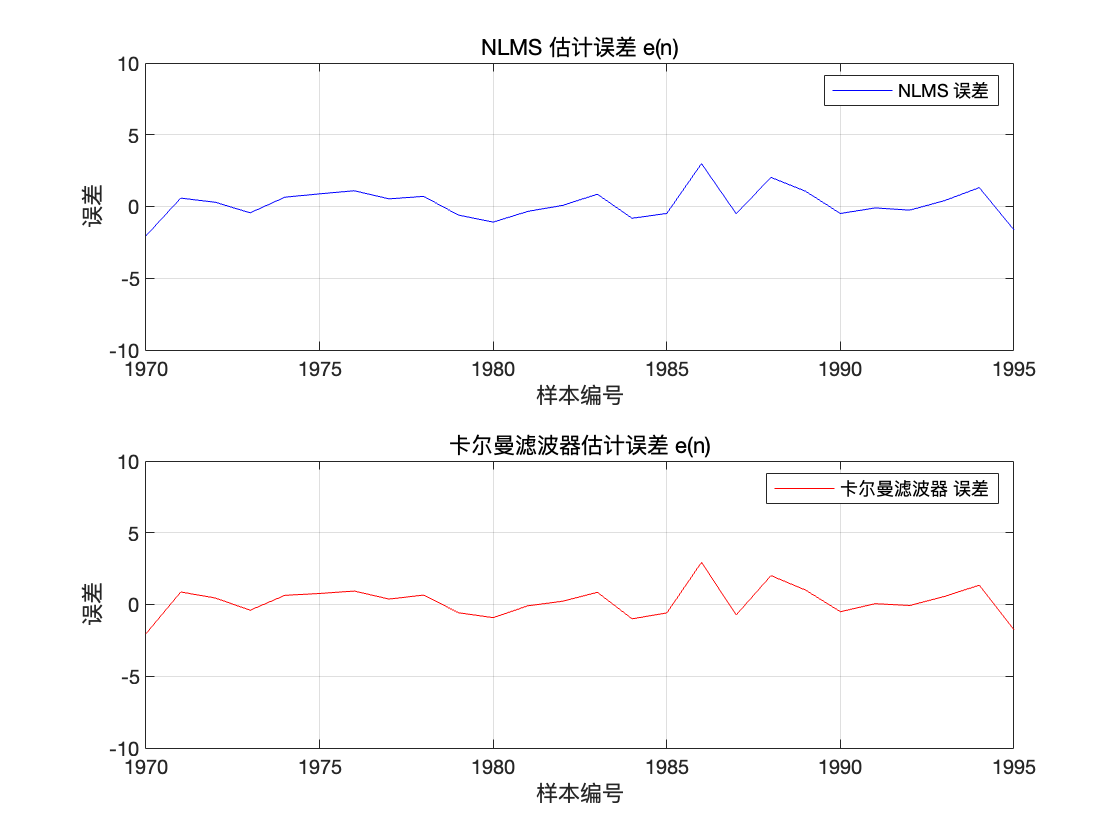
从图中可见,无论是 NLMS 还是卡尔曼滤波,误差的平均值都接近于 0,说明它们在整体上对信号已经预测得相当好。之所以来回波动,是因为输入信号本身是随机 AR 过程,且仍然带有噪声影响。
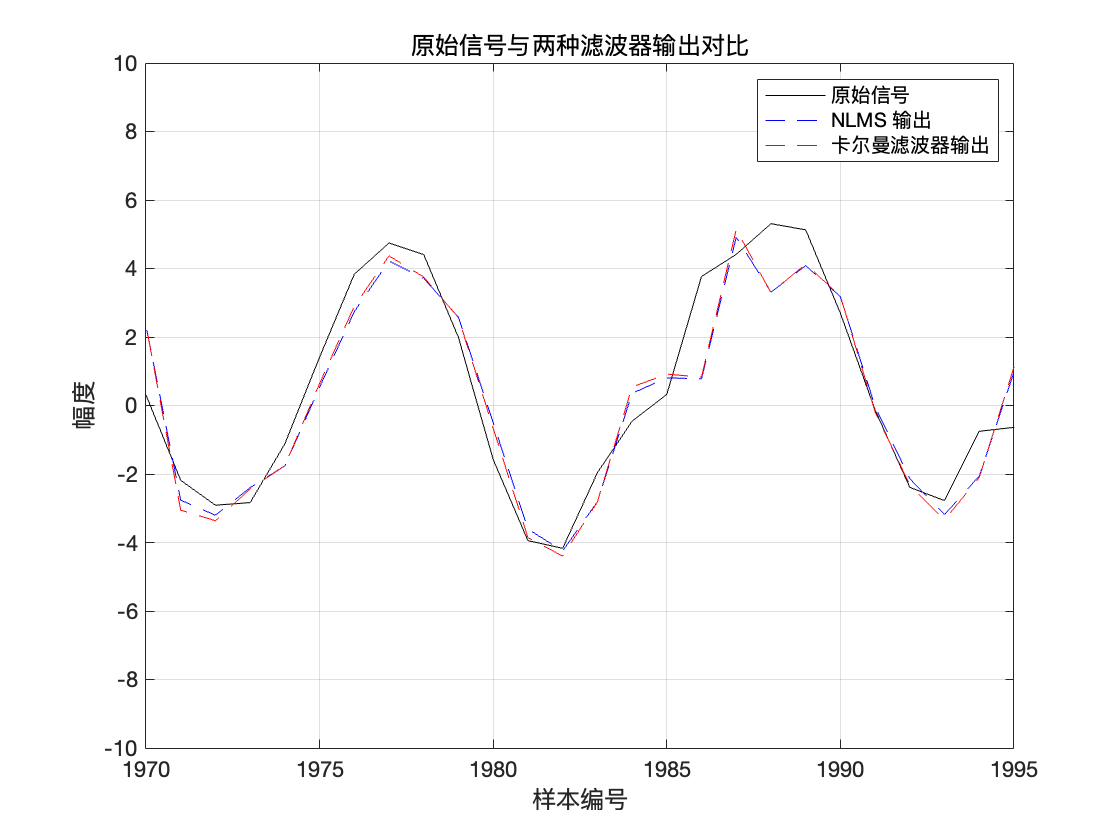
NLMS 和 卡尔曼 都能比较好地追踪到波形变化中的波峰波谷位置,说明两种算法都能够获取到较准确的 AR 参数,对信号进行了成功的预测。从视觉精度上来看两个算法准确度差不多。
综上所述,整个过程从 AR 模型出发,将参数估计问题转化为对输入向量和参数向量的线性映射求解,再利用 NLMS 和卡尔曼滤波两种不同的自适应估计策略实现参数在线更新。NLMS 通过归一化步长提高收敛稳健性,而卡尔曼滤波则将问题纳入统计最优估计框架中,实现更精确的参数识别。
滤波器步长的影响
在 NLMS 中,滤波器系数向量\mathbf{h}(k) 的更新公式为:
在这个公式中,步长\mu 决定收敛速度与稳态误差之间的权衡:
\mu 较大:收敛速度快但稳态精度较差,容易产生跳跃式的尝试,可能跃过最优解
\mu 较小:稳态精度高但收敛缓慢,需要更多迭代才能收敛,计算量大,时间成本高。
在上述内容中,我们令\mu = 0.01
(b) 卡尔曼滤波没有波长,它在每一时刻都自动计算一个最优增益K(k) ,不需要手动设置步长来控制更新幅度,这也是卡尔曼滤波器的重要优点。但是它可以通控制 过程噪声协方差Q 与 测量噪声协方差R 来平衡滤波的“收敛速度-精度”。
过程噪声协方差\mathbf{Q} 大时 ,滤波器更倾向快速响应参数变化,因此对先验预测的权重降低,对新观测值的权重加大。
测量噪声协方差\mathbf{R} 小时,滤波器会更信任当前观测数据,可以将卡尔曼增益K(k) 增大。
目标跟踪
实现 Singer 类型轨迹生成器
编写 MATLAB 函数,用于生成基于理论课程中关于状态空间表示的理论发展而来的 Singer 类型噪声轨迹。
“模型噪声”向量将由函数 \text{randn} 生成。由于其协方差矩阵不是对角矩阵,因此需要引入向量分量之间的相关性。为此,利用函数 \text{chol} 。解释如何结合函数 \text{randn} 和 \text{chol} 以生成预期的“模型噪声”向量的统计特性。
我们选择轨迹使得沿 x 轴和 y 轴的坐标相互独立且类型相同。假设对象最初位于原点,其坐标为(0, 0)。
Singer 模型依赖一个参数,通常记为 \alpha ,表示加速度自相关函数的下降方式。研究该参数的多个值及其对生成轨迹的影响。
在一张图中,展示对象沿 Singer 模型运动的多次实现。观察数 N 设为 500,采样周期取为1 秒。加速度和 jerk 的方差将由二元组选择,并需在报告中说明。提供三张图,每张图对应一个 \alpha 值。
根据未受噪声影响的位置信息(即状态向量中随时间变化的一个分量),给出一种估计速度和加速度的方法。将这些估计值与生成的速度和加速度值(状态向量中另外两个分量)进行比较。如果位置信息受噪声影响,该方法是否仍然适用?
画出基于估计加速度分量的自相关函数,并与理论形状进行比较。
理论部分
Singer 模型的连续时间描述
在课程理论中,Singer 模型中的加速度过程不再是白噪声,而是带有相关性的过程,其自相关函数 为
其中\tau_m = \tfrac{1}{\alpha},衰减系数为\alpha。
由功率谱关系可得加速度满足以下微分方程,得到连续时间下的加速度 \ddot{x}(t) 满足
其中w(t)为方差q = \tfrac{2\,\sigma_m^2}{\tau_m}的零均值白噪声 。令\alpha = \frac{1}{\tau_m},则上式也可写为
Singer 模型的状态空间表示
将位置x(t)、速度\dot{x}(t)、加速度\ddot{x}(t) 组成状态向量
则其连续状态方程可写为:
将上式在采样周期T下离散化
其中
Phi = compute_phi(alpha, T); % 状态转移矩阵
离散系统的过程噪声 \mathbf{w}_k 并非分量独立,而是协方差矩阵 Q 给出相应的耦合关系:
而协方差矩阵Q 则可以通过积分或相应推导得到:
若\alpha 趋于 0 或\infty,会退化为匀加速 (MUA) 或匀速直线 (MRU) 的情况。
Q = compute_Q(alpha, T, sigma_m); % 过程噪声协方差矩阵
Cholesky 分解原理
对给定 Q ,用 chol(Q) 求得下三角矩阵 \mathbf{L}
L = chol(Q, 'lower'); % 分解 Q 得到 L,使得 Q = L * L^T
因此我们有:
原公式变成:
x_state = Phi * x_state + w_x;
y_state = Phi * y_state + w_y;
接下来,我们选择轨迹使得沿x 轴和y 轴的坐标相互独立且类型相同。假设对象最初位于原点,其坐标为(0, 0)
当x、 y 方向解耦时,可分别为x 方向与y 方向建立一维 Singer 模型:
\mathbf{x}_k^{(x)} = \begin{bmatrix} x \\[2pt] \dot{x} \\[2pt] \ddot{x} \end{bmatrix} \quad \mathbf{x}_k^{(y)} = \begin{bmatrix} y \\[2pt] \dot{y} \\[2pt] \ddot{y} \end{bmatrix}初始位置为(0,0),即初始状态向量为 [0,\,0,\,0]^T 在两轴上分别独立生成轨迹,再拼合成二维运动。
% 生成单条真实轨迹(只取x方向作为示例)
[positions_single, velocities_single, accelerations_single] = generate_singer_trajectory(alpha, T, num_steps, Phi, Q, 1);
Singer 模型依赖一个参数,通常记为\alpha,表示加速度自相关函数的下降方式,由公式 \alpha = 1/\tau_m 可知, \alpha 大意味着加速度自相关衰减得快,运动的随机抖动更大, \alpha 小则轨迹更平滑。
观察数N 设为 500,采样周期取为 1 秒,分别取\alpha = 1,\,0.1,\,0.01 来展示对象沿 Singer 模型运动的不同实现。
加速度的选择:
sigma_m = 1; % 加速度标准差jerk方差的选择:
将 jerk 看作 加速度的一阶导数,其随机特性本质上由同一个过程噪声w(t) 决定。 换句话说,jerk 的方差 在离散实现中被自动包进了
compute_Q(alpha, T, sigma_m)的结果里
无噪声位置信息来估计速度与加速度
速度估计:采用最简单的差分方法
est_v_x = diff(x_pos)/T; % 用相邻位置之差除以采样周期,得到速度的估计
加速度估计:对上一步得到的速度再做一次差分
est_a_x = diff(est_v_x)/T; % 二次差分得到加速度估计
真实速度: x_vel
真实加速度: x_acc
% 真实位置、速度、加速度(无噪声)
x_pos = positions_single(1,:,1);
x_vel = velocities_single(1,:,1);
x_acc = accelerations_single(1,:,1);
获得 真实v_k, a_k。在图上可对比估计值\hat{v}_k, \hat{a}_k 与真实值v_k, a_k 来观察误差。
有噪声位置信息来估计速度与加速度
如果位置本身含噪声,差分运算会放大噪声,从而导致速度、加速度的估计精度下降。特别是当噪声较大或统计特性复杂时,估计的 \hat{v}(k) 和 \hat{a}(k) 会显著偏离真实速度 x_vel 、真实加速度 x_acc 。
画出基于估计加速度分量的自相关函数,并与理论形状进行比较。
在 MATLAB 中可对离散\hat{a}[k] 做加速度自相关估计,其自相关估计值为:
可通过 xcorr(...,'unbiased') 函数来无偏估计自相关函数:
[acf_est, lags] = xcorr(x_acc, 'unbiased'); % 计算加速度的无偏自相关
返回估计自相关函数 acf_est 以及对应的滞后量 lags (整数索引)。若采样周期为 T ,则实际时间延迟为
lags_time = lags * T;
我们和加速度自相关理论值做对比:
tau_m = 1 / alpha; % 自相关时间常数
r_theo = sigma_m^2 * exp(-abs(lags_time)/tau_m); % 理论自相关函数
这样即可得到与 acf_est 处于同一横轴 (时间延迟) 维度上的理论值 r_theo 。
用同一个坐标系绘制 acf_est 和r_theo ,对比形状和幅值。
完整代码如下:
%% 部分2:目标跟踪
clear all ;clc;close all
%% 步骤1:实现Singer类型轨迹生成器
% 本部分生成Singer模型下的目标运动轨迹,并叠加测量噪声,随后分析不同参数对轨迹特性的影响。
% 定义参数
N = 3; % 显示3条不同轨迹的实现
T = 1; % 采样周期
total_time = 500; % 总仿真时长
num_steps = total_time / T; % 将总时间除以采样周期得到离散的时间步数。
alpha = 1; % Singer模型的alpha参数,用于控制加速度自相关函数的衰减率
sigma_m = 1; % 加速度过程噪声的标准差
% 计算状态转移矩阵Phi和Q(根据Singer模型理论公式)
Phi = compute_phi(alpha, T); % 状态转移矩阵
Q = compute_Q(alpha, T, sigma_m); % 过程噪声协方差矩阵
% 准备存储真实位置(不含测量噪声)和测量位置(含噪声)
true_positions = zeros(N, num_steps);
measured_positions = zeros(N, num_steps);
% 生成轨迹
for realization = 1:N
% 用给定的 Φ,Q 及初始状态生成单条目标真实运动轨迹(只取x方向作为示例)
[positions_single, ~, ~] = generate_singer_trajectory(alpha, T, num_steps, Phi, Q, 1);
% 提取x方向的真实位置
true_position = positions_single(1, :, 1);
% 加入高斯测量噪声
measurement_noise_std = 50; % 观测噪声(测量噪声)的标准差
measured_position = true_position + measurement_noise_std * randn(size(true_position));
% 存储生成的"真实轨迹"与“加了噪声的测量轨迹”
true_positions(realization, :) = true_position;
measured_positions(realization, :) = measured_position;
end
% 绘制真实轨迹(实线)和测量轨迹(虚线)进行对比
figure;
hold on; grid on;
for realization = 1:N
plot(1:num_steps, true_positions(realization, :), 'LineWidth', 1.5, 'DisplayName', sprintf('真实位置 实现 %d', realization));
plot(1:num_steps, measured_positions(realization, :), '--', 'LineWidth', 1.5, 'DisplayName', sprintf('测量位置 实现 %d', realization));
end
title(sprintf('Singer信号的三次实现 (\\alpha = %.2f)', alpha));
xlabel('时间步 k');
ylabel('位置');
legend;
hold off;
%% 分析不同alpha值对生成轨迹的影响
% 通过改变alpha观察轨迹的平滑度和加速度特性变化
alpha_values = [1, 0.1, 0.01];
for k = 1:length(alpha_values)
alpha = alpha_values(k);
% 根据该alpha计算Phi和Q
Phi = compute_phi(alpha, T);
Q = compute_Q(alpha, T, sigma_m);
% 生成轨迹(单条实现)
[positions_single, velocities_single, accelerations_single] = generate_singer_trajectory(alpha, T, num_steps, Phi, Q, 1);
% 提取x方向真实位置
true_position = positions_single(1, :, 1);
% 生成有噪声测量位置
measured_position = true_position + measurement_noise_std * randn(size(true_position));
% 绘图对比
figure;
plot(1:num_steps, true_position, 'b', 'LineWidth', 2); hold on;
plot(1:num_steps, measured_position, 'r--', 'LineWidth', 2);
title(sprintf('真实位置 vs 测量位置 (\\alpha = %.4f)', alpha));
xlabel('时间步 k');
ylabel('位置');
legend('真实位置', '测量位置');
grid on;
hold off;
end
%% 在无噪声条件下估计速度与加速度 (alpha = 1)
% 利用无噪声条件下的轨迹,使用简单差分法估计速度和加速度,并与真实值比较
alpha = 1;
Phi = compute_phi(alpha, T);
Q = compute_Q(alpha, T, sigma_m);
% 生成轨迹
[positions_single, velocities_single, accelerations_single] = generate_singer_trajectory(alpha, T, num_steps, Phi, Q, 1);
% 真实位置、速度、加速度(无噪声)
x_pos = positions_single(1,:,1);
x_vel = velocities_single(1,:,1);
x_acc = accelerations_single(1,:,1);
% 用差分近似速度和加速度
est_v_x = diff(x_pos)/T; % 一阶差分估计速度
est_a_x = diff(est_v_x)/T; % 二阶差分估计加速度
% 绘制速度与加速度比较
figure;
subplot(2,1,1);
plot(1:num_steps, x_vel, 'b', 1:(num_steps-1), est_v_x, 'r--');
legend('真实速度','估计速度'); title('速度比较'); grid on;
xlabel('时间步'); ylabel('速度');
subplot(2,1,2);
plot(1:num_steps, x_acc, 'b', 1:(num_steps-2), est_a_x, 'r--');
legend('真实加速度','估计加速度'); title('加速度比较'); grid on;
xlabel('时间步'); ylabel('加速度');
%% 自相关函数及理论比较
% 利用估计的加速度信号计算其自相关函数,并与理论给定的指数衰减相关函数比较。
% 自相关的估计与理论值的匹配度越高,说明模型与实现越接近。
alpha = 1;
[acf_est, lags] = xcorr(x_acc, 'unbiased'); % 计算加速度的无偏自相关
lags_time = lags * T;
tau_m = 1/alpha; % tau_m定义为1/alpha
r_theo = sigma_m^2 * exp(-abs(lags_time)/tau_m); % 理论自相关函数
figure;
plot(lags_time, acf_est, 'b', lags_time, r_theo, 'r--');
legend('估计的ACF','理论ACF');
xlabel('\tau (s)'); ylabel('r_{aa}(\tau)');
title('加速度自相关函数比较');
grid on;
function phi = compute_phi(alpha,T)
% 作用:
% 根据 Singer 模型的离散化公式,构造状态转移矩阵 Phi。
%
% 输入:
% alpha - Singer 模型的衰减率 (alpha = 1 / tau_m)
% T - 离散采样周期
%
% 输出:
% phi - 3 x 3 的状态转移矩阵 (离散形式)
%
p3 = (1 / alpha^2) * (-1 + alpha*T + exp(-alpha*T));
p6 = (1 / alpha) * (1 - exp(-alpha*T));
p9 = exp(-alpha*T);
phi = [1, T, p3;
0, 1, p6;
0, 0, p9];
end
function Q = compute_Q(alpha, T, sigma_m)
% 作用:
% 根据 Singer 模型的解析公式,给出离散系统中三维状态 [x; v; a] 对应的过程噪声协方差矩阵 Q。
%
% 输入:
% alpha - Singer 模型参数(加速度指数衰减率,alpha = 1 / tau_m)
% T - 离散采样周期
% sigma_m - 加速度过程噪声的标准差
%
% 输出:
% Q - 3 x 3 的过程噪声协方差矩阵
% 根据 Singer 模型的推导公式分块计算过程噪声协方差矩阵的各个元素
q11 = (1/ (2*alpha^5)) * (2*alpha*T - 2*alpha^2*T^2 + 2*alpha^3*T^3/3 - 4*alpha*T*exp(-alpha*T) - exp(-2*alpha*T) + 1);
q12 = (1 / (2*alpha^4)) * (alpha^2*T^2 + 1 + exp(-2*alpha*T) + exp(-alpha*T)*(-2+2*alpha*T) - 2*alpha*T);
q13 = (1 / (2*alpha^3)) * (1 - 2*alpha*T*exp(-alpha*T) - exp(-2*alpha*T));
q22 = (1 / (2*alpha^3)) * (2*alpha*T - 3 + 4*exp(-alpha*T) - exp(-2*alpha*T));
q23 = (1 / (2*alpha^2)) * (1 - exp(-alpha*T))^2;
q33 = (-1 / (2*alpha)) * (exp(-2*alpha*T) -1);
Q = 2 * alpha * sigma_m^2 * [q11, q12, q13;
q12, q22, q23;
q13, q23, q33];
Q = (Q + Q') / 2; % 保证矩阵数值上的对称性
end
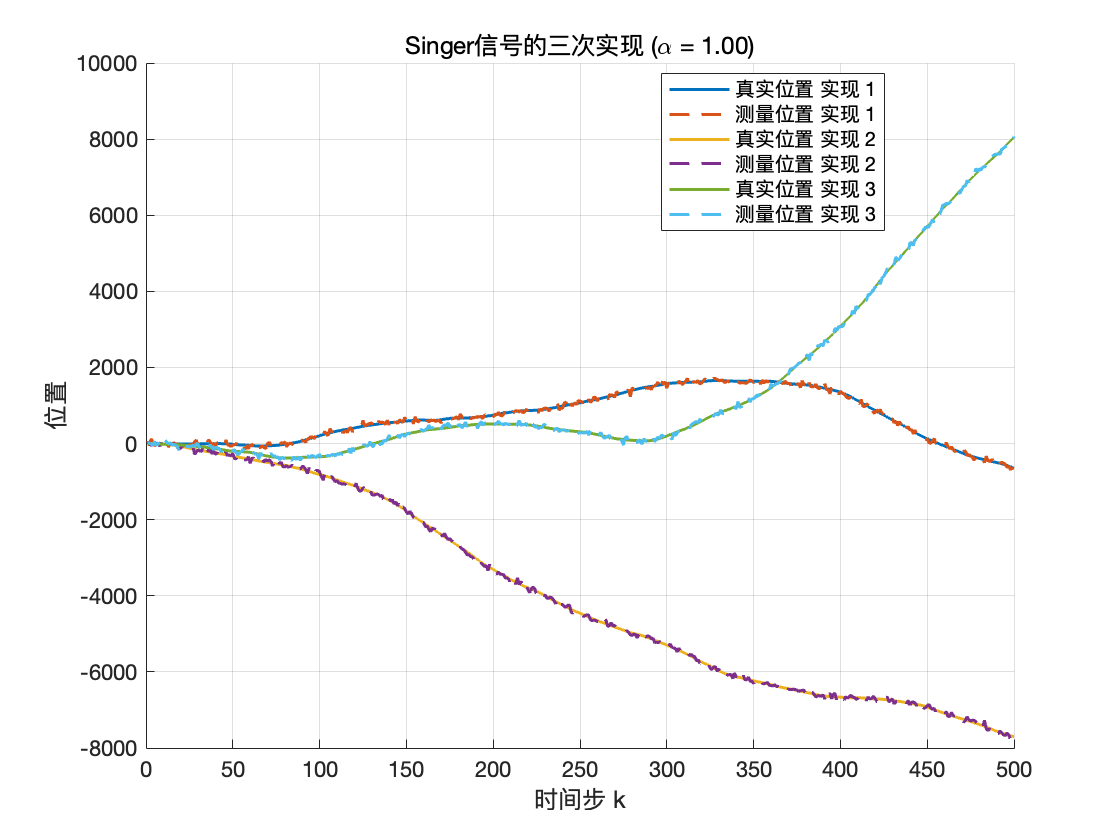
在\alpha =1 的时候,可见测量位置紧随真实位置的总体走势,局部会产生随机波动或偏移,这是因为在真实位置的基础上叠加测量噪声后才得到观测值。 Singer 模型中\alpha 影响着加速度的自相关时间、加速度变化,轨迹平滑度。
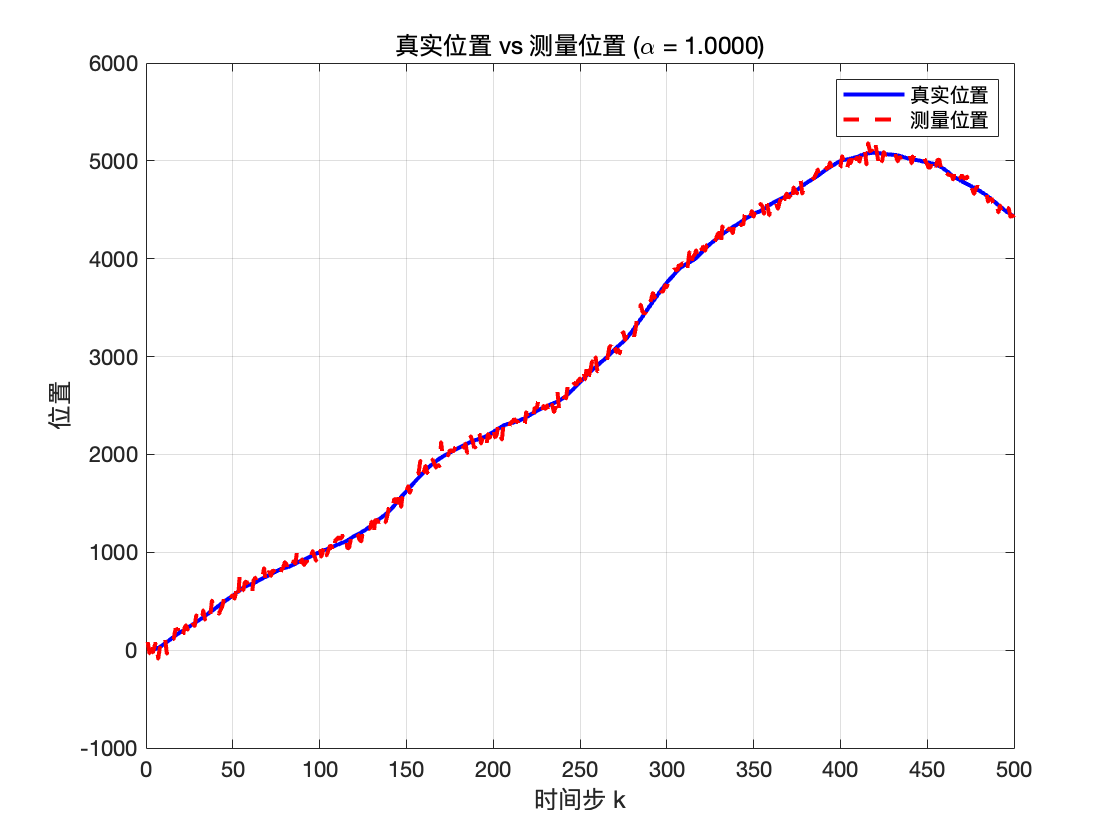
我们单独拿出来一个轨迹观察,可见\alpha 过大,导致波动较大,我们尝试减少\alpha
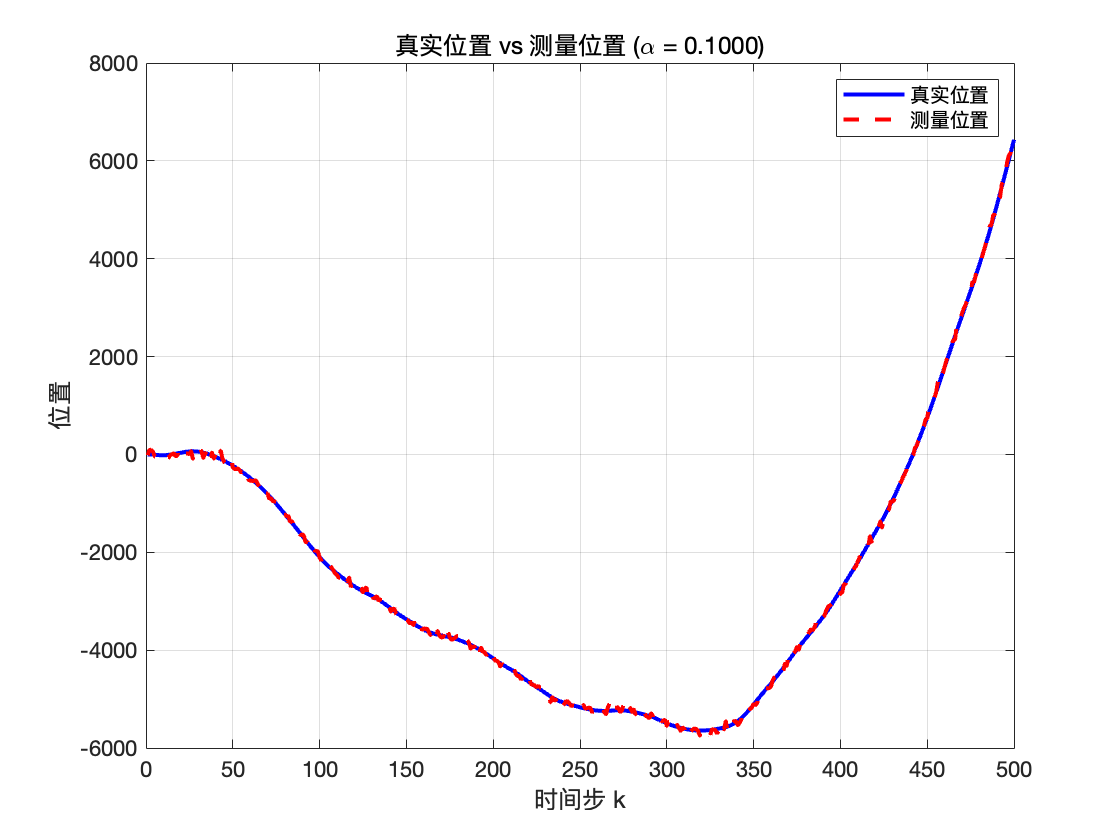
我们将\alpha 越小,会导致加速度的自相关时间变长、加速度变化缓慢,轨迹更平滑,但是在细节处仍会有细微的波动,我们继续尝试减少\alpha 。
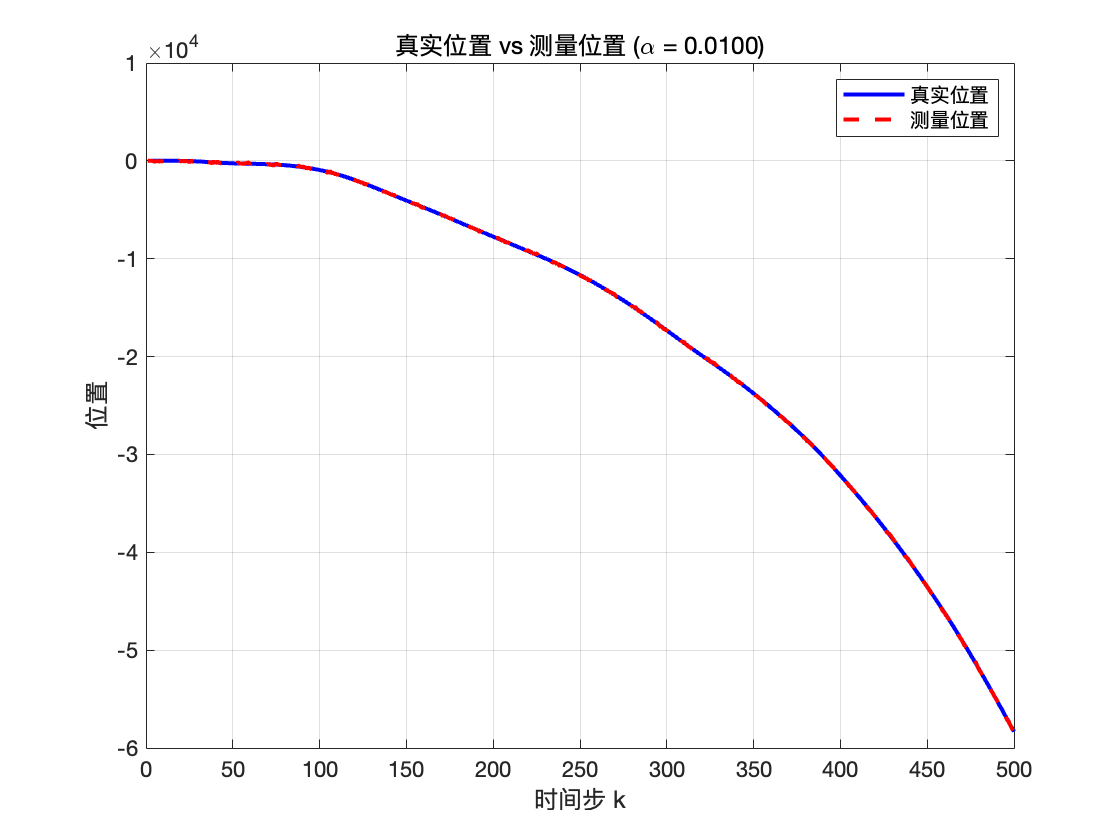
\alpha 越大,则加速度的随机变化更频繁、轨迹看起来抖动, \alpha 值越小,说明加速度保持相关的时间越长,轨迹更加平滑
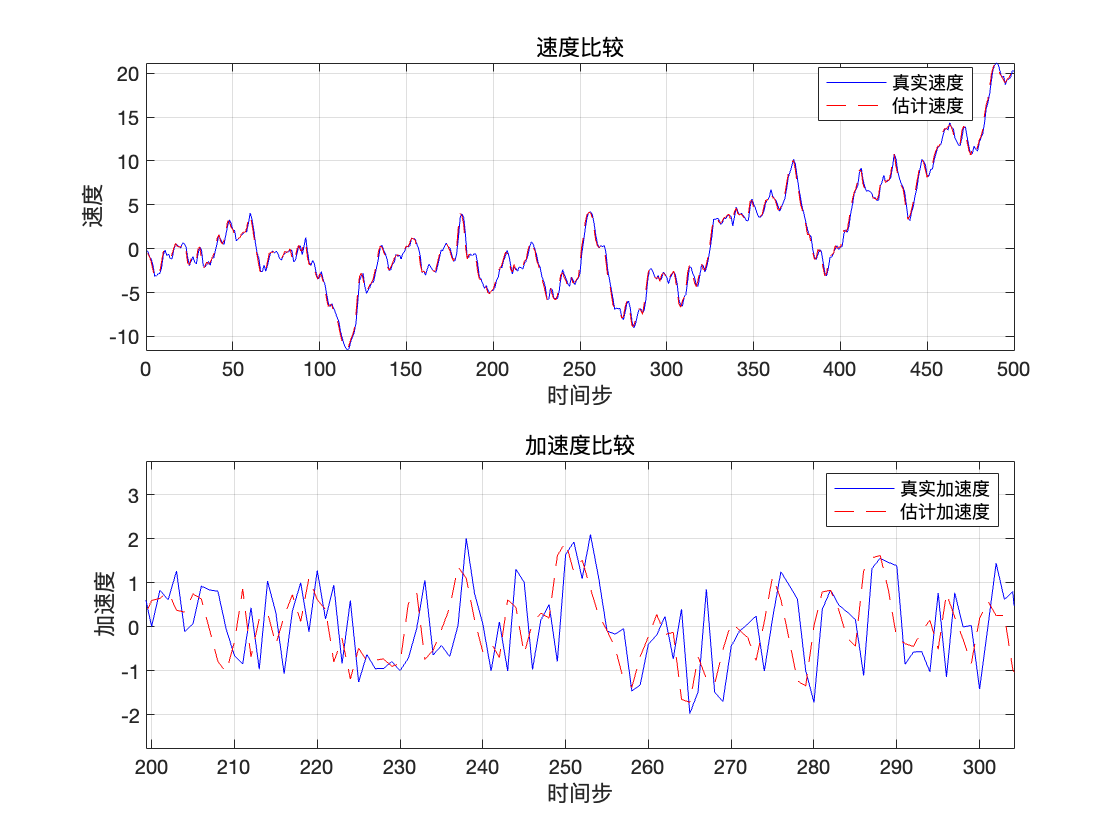
可见估计速度是完美贴合真实速度,而加速度的估计符合真实值轮廓
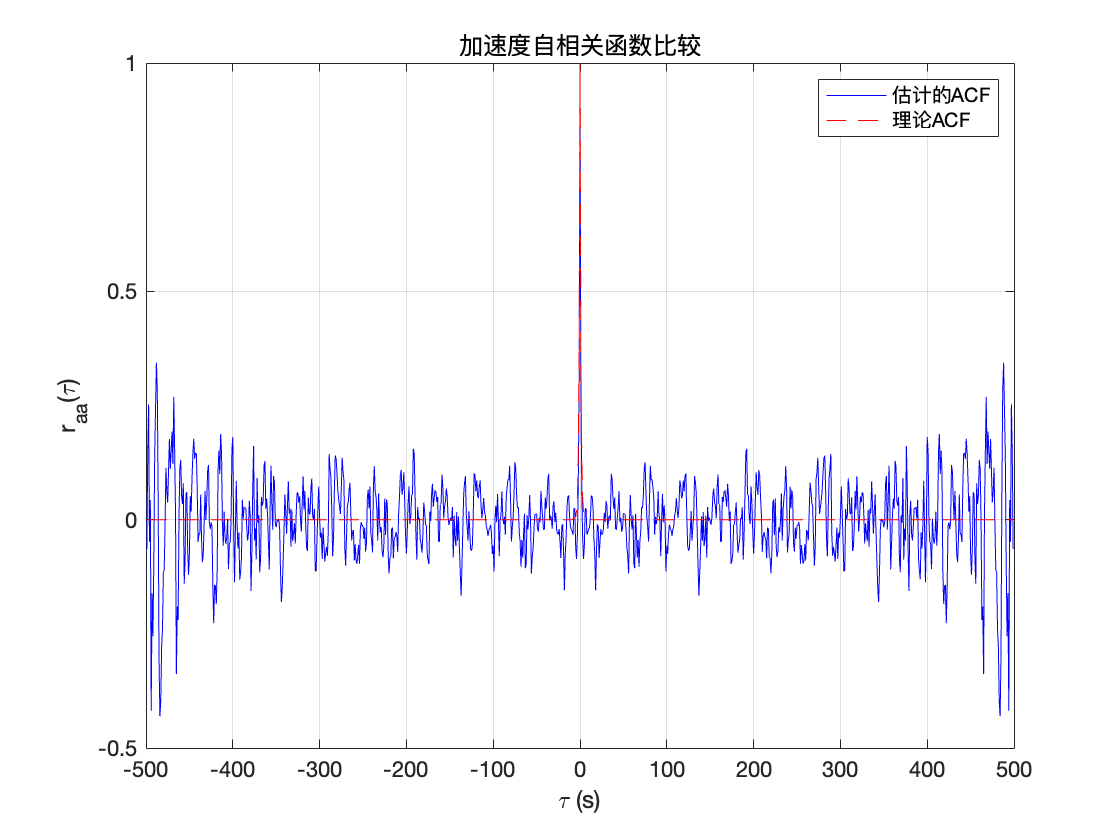
. 理论的加速度自相关函数 在中心处( \tau=0)值等于1,估计曲线也很好的得出了这一点,当\tau 远离中心 时,理论上的自相关会呈现指数衰减并接近于 0,而估计曲线也围绕 0 上下随机抖动。
卡尔曼滤波 对带噪Singer 进行轨迹估计
我们假设之前通过 Singer 模型 获取到的所有状态空间矩阵(如状态转移矩阵\Phi、过程噪声协方差矩阵Q、测量矩阵H、测量噪声协方差R 等)均为已知且准确。然后我们对这个 带噪声的 Singer 轨迹应用卡尔曼滤波,并对比:
理论无噪声轨迹
带噪声测量值轨迹
卡尔曼滤波估计轨迹
此外,还使用 蒙特卡洛方法 进行多次重复实验,从而综合评估卡尔曼滤波器的性能。
卡尔曼滤波理论回顾
Singer 模型在离散形式下可写为:
在这里,我们认为\Phi 和Q 在整个滤波过程中是已知并固定的。
测量方程可表示为:
其中,在本例中我们只测量了位置,测量维数为 1:
卡尔曼滤波的预测与更新方程我们在之前已经详细解释过,我们直接给出对应公式:
预测阶段
\mathbf{x}(k\mid k-1) = \Phi \,\mathbf{x}(k-1\mid k-1), \quad P(k\mid k-1) = \Phi\,P(k-1\mid k-1)\,\Phi^T + Q更新阶段
\begin{aligned} \mathbf{K}(k) \;&=\; P(k\mid k-1)\,H^T\Bigl(H\,P(k\mid k-1)\,H^T + R\Bigr)^{-1}\\ \mathbf{x}(k\mid k) \;&=\; \mathbf{x}(k\mid k-1) \;+\; \mathbf{K}(k)\Bigl(\mathbf{z}(k) - H\,\mathbf{x}(k\mid k-1)\Bigr)\\ P(k\mid k) \;&=\;\bigl(I - \mathbf{K}(k)\,H\bigr)\,P(k\mid k-1) \end{aligned}
带噪声轨迹的卡尔曼滤波实现
%% 3.2 第2步:卡尔曼滤波(标称情况)
% 在此步骤中对一条带噪声的轨迹实施卡尔曼滤波,并同时绘制理论无噪声轨迹、
% 带噪声轨迹以及卡尔曼滤波估计的轨迹。
% 状态定义为 [x; vx; ax],测量为x
% 因此nx=3, nz=1
nx = 3;
nz = 1;
% 基本参数(与之前一致)
T = 1;
total_time = 500;
num_steps = total_time / T;
alpha = 1;
sigma_m = 1;
sigma_r = 50; % 测量噪声标准差
% 计算Singer模型的Phi和Q(需要对应3维状态)
% 在x方向上的Singer模型状态为:[x; vx; ax]
% 对应的状态转移矩阵Phi和Q应根据x方向Singer模型推导获得。
% 这里假设compute_phi和compute_Q可以返回x方向3维状态的Phi和Q矩阵。
Phi = compute_phi(alpha, T); % 应返回 3x3 矩阵
Q = compute_Q(alpha, T, sigma_m); % 应返回3x3的Q矩阵
% 测量矩阵H,只观测位置x,所以H = [1 0 0]
H = [1 0 0];
% 测量噪声R
R = sigma_r^2;
% 初始状态和方差
x0 = [0;0;0]; % 假设初始位置、速度、加速度为0
P0 = 1e4*eye(nx);
% 生成无噪声理论轨迹及有噪声测量
[positions_single, velocities_single, accelerations_single] = generate_singer_trajectory(alpha, T, num_steps, Phi, Q, sigma_m);
x_true = positions_single(1,:,1); % 无噪声x位置
x_meas = x_true + sigma_r*randn(size(x_true)); % 有噪声测量
% 卡尔曼滤波实现(单次实现)
x_hat = zeros(nx, num_steps);
P_hat = zeros(nx, nx, num_steps);
x_hat(:,1) = x0;
P_hat(:,:,1) = P0;
for k = 2:num_steps
% 预测
x_pred = Phi * x_hat(:,k-1);
P_pred = Phi * P_hat(:,:,k-1) * Phi' + Q;
% 当前测量
z_k = x_meas(k);
% 卡尔曼增益
S = H * P_pred * H' + R;
K = P_pred * H' / S;
% 更新
x_hat(:,k) = x_pred + K*(z_k - H*x_pred);
P_hat(:,:,k) = (eye(nx)-K*H)*P_pred;
end
% 抽取估计位置
x_est = x_hat(1,:);
% 绘制理论无噪声轨迹、有噪声测量和卡尔曼滤波估计
figure; hold on; grid on;
plot(1:num_steps, x_true, 'k', 'DisplayName', '理论无噪声轨迹');
plot(1:num_steps, x_meas, 'rx', 'DisplayName', '有噪声测量');
plot(1:num_steps, x_est, 'b', 'LineWidth', 1.5, 'DisplayName', '卡尔曼滤波估计');
xlabel('时间步');
ylabel('位置');
title('理论轨迹、测量值与卡尔曼滤波估计比较(x方向)');
legend;
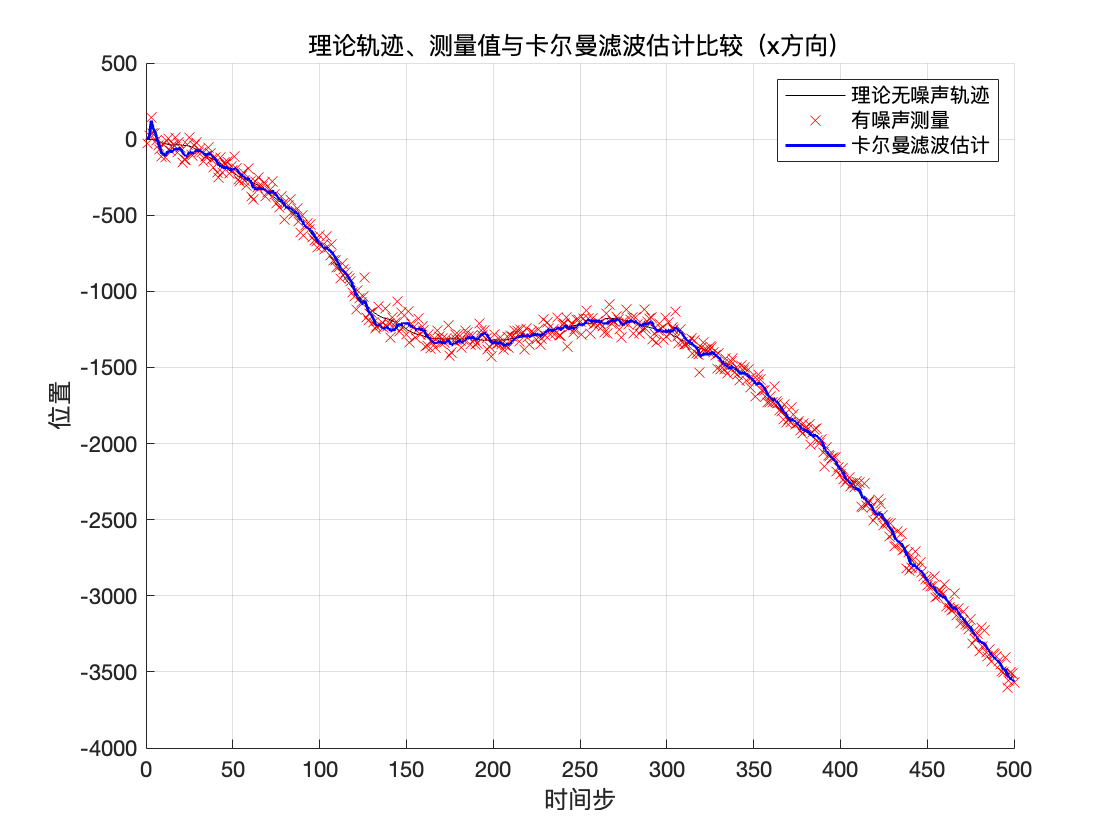
理论无噪声轨迹 是根据 Singer 模型在仿真中生成的“真实”运动轨迹,不含测量噪声,代表理想情况下目标的实际位置随时间的演变。
有噪声测量轨迹 是在真实轨迹的基础上叠加了高斯测量噪声得到的观测值
卡尔曼滤波估计轨迹 是对有噪声的测量数据应用卡尔曼滤波后,输出的目标位置估计。该估计在多数时间步上接近理论轨迹,比原始测量值更加平滑、且误差更小。
为评估卡尔曼滤波器在随机噪声下的表现,我们对 Singer 模型 做多次( N_{bMC} 次)重复仿真,每次均生成新的噪声轨迹并执行卡尔曼滤波。然后在每个时间步计算并记录以下均方根误差(RMSE)指标:
测量噪声的均方根误差REQM_{\mathrm{mesure}}(n)
REQM_{\mathrm{mesure}}(n) \;=\; \sqrt{ \frac{1}{N_{bMC}} \sum_{i=1}^{N_{bMC}} \Bigl(\mathbf{X}_{\mathrm{mesure},i}(n) \;-\; \mathbf{X}_{\mathrm{verity},i}(n)\Bigr)^T \Bigl(\mathbf{X}_{\mathrm{mesure},i}(n) \;-\; \mathbf{X}_{\mathrm{verity},i}(n)\Bigr) }卡尔曼滤波估计位置的均方根误差REQM_{\mathrm{Kalman}}(n)
REQM_{\mathrm{Kalman}}(n) \;=\; \sqrt{ \frac{1}{N_{bMC}} \sum_{i=1}^{N_{bMC}} \Bigl(\mathbf{X}_{\mathrm{Kalman},i}(n) \;-\; \mathbf{X}_{\mathrm{verity},i}(n)\Bigr)^T \Bigl(\mathbf{X}_{\mathrm{Kalman},i}(n) \;-\; \mathbf{X}_{\mathrm{verity},i}(n)\Bigr) }
其中, \mathbf{X}(n) 在本例中为一维标量,因为我们只估计 x 方向上的轨迹
以下 MATLAB 代码给出了具体的蒙特卡洛实现流程与画图操作示例。最终会得到两个随时间步变化的 RMSE 曲线,用以比较 测量值 与 卡尔曼滤波估计 相对于无噪声参考轨迹的误差大小。
%% ========== 蒙特卡罗评估卡尔曼滤波性能 ==========
N_BMC = 50; % 蒙特卡罗次数,可根据需要调整
REQM_mesure = zeros(num_steps, 1);
REQM_kalman = zeros(num_steps, 1);
for iMC = 1:N_BMC
[pos_i,~,~] = generate_singer_trajectory(alpha, T, num_steps, Phi, Q, sigma_m);
x_true_i = pos_i(1,:,1);
x_meas_i = x_true_i + sigma_r*randn(size(x_true_i));
x_hat_i = zeros(nx, num_steps);
P_hat_i = zeros(nx, nx, num_steps);
x_hat_i(:,1) = x0;
P_hat_i(:,:,1) = P0;
for k = 2:num_steps
x_pred_i = Phi * x_hat_i(:,k-1);
P_pred_i = Phi * P_hat_i(:,:,k-1) * Phi' + Q;
z_k_i = x_meas_i(k);
S_i = H * P_pred_i * H' + R;
K_i = P_pred_i * H' / S_i;
x_hat_i(:,k) = x_pred_i + K_i*(z_k_i - H*x_pred_i);
P_hat_i(:,:,k) = (eye(nx)-K_i*H)*P_pred_i;
end
x_est_i = x_hat_i(1,:);
for n = 1:num_steps
X_verite = x_true_i(n);
X_mesure = x_meas_i(n);
X_kalman = x_est_i(n);
% 对于一维数据,(X_mesure - X_verite)^T(X_mesure - X_verite)即 (x_meas - x_true)^2
REQM_mesure(n) = REQM_mesure(n) + (X_mesure - X_verite)^2;
REQM_kalman(n) = REQM_kalman(n) + (X_kalman - X_verite)^2;
end
end
REQM_mesure = sqrt(REQM_mesure / N_BMC);
REQM_kalman = sqrt(REQM_kalman / N_BMC);
% 绘制REQM结果对比
figure; hold on; grid on;
plot(1:num_steps, REQM_mesure, 'r', 'DisplayName', 'REQM_{mesure}(n)');
plot(1:num_steps, REQM_kalman, 'b', 'DisplayName', 'REQM_{kalman}(n)');
xlabel('时间步 n');
ylabel('REQM');
title('测量与卡尔曼滤波估计的REQM比较(x方向)');
legend;
disp('卡尔曼滤波标称情况下的蒙特卡罗统计完成:');
disp('REQM_mesure和REQM_kalman已计算完成。');
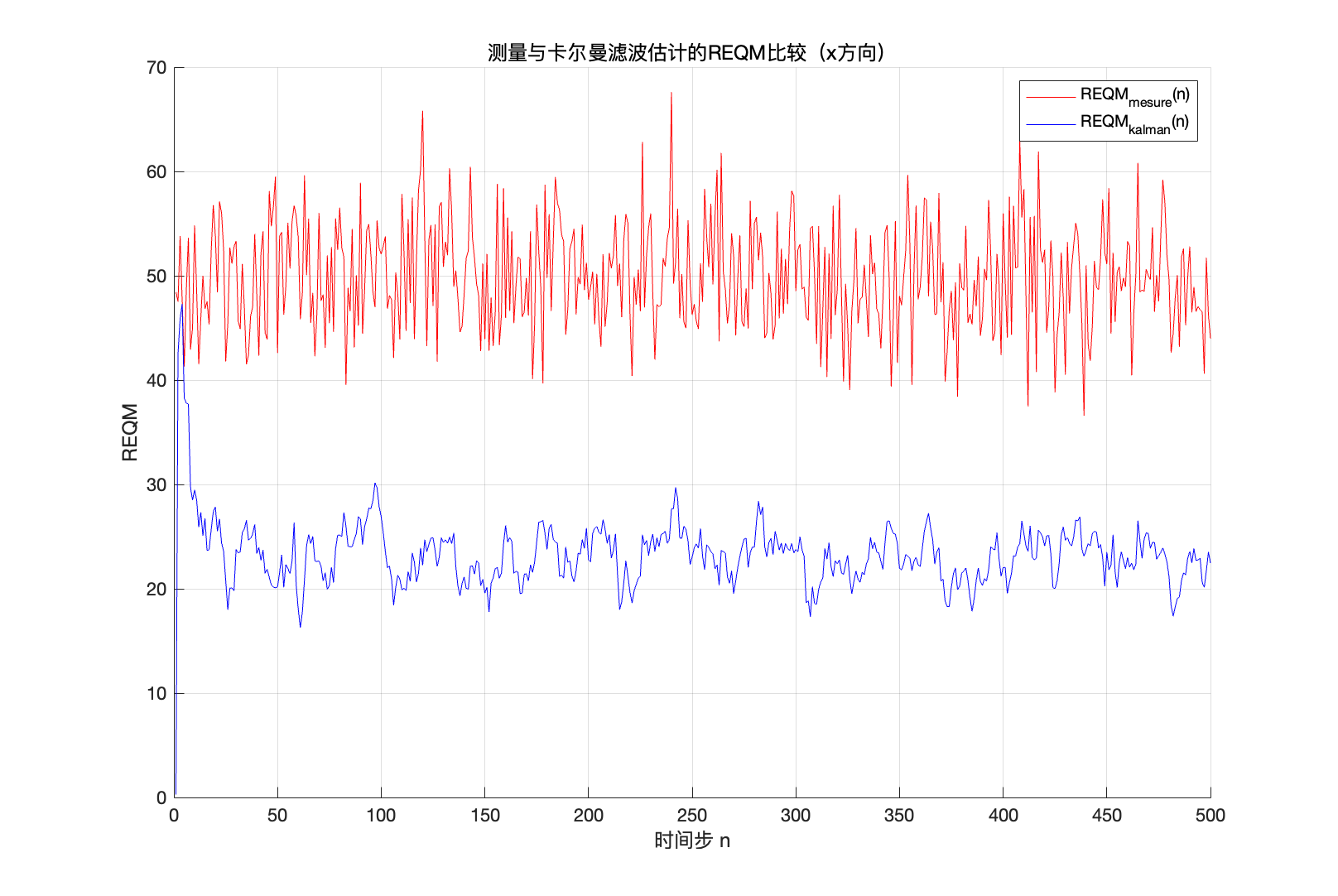
从上图可以看出,卡尔曼滤波在绝大多数时间步上的 RMSE 通常要低于直接测量值对应的 RMSE,体现了卡尔曼滤波对噪声的抑制能力。
在刚开始时,卡尔曼滤波和系统状态还没有完全混熟,估计误差相对较大;随着滤波迭代进行,卡尔曼增益等状态协方差矩阵逐渐收敛,估计逐步贴近真值,使得误差下降并稳定。
卡尔曼滤波(非标称情况)
在这一阶段,我们考虑 非标称(不匹配) 的滤波器模型假设,即卡尔曼滤波器中所用的 模型噪声协方差 或 Singer 模型参数\alpha 与真实生成轨迹时所用的参数不一致,具体包括:
模型噪声方差\sigma_m 的错误估计:
在仿真中,真实模型噪声标准差为\sigma_m^\text{true},但卡尔曼滤波器中使用的噪声水平\sigma_m^\text{filt} 与真实值不符。
我们会高估或低估真实\sigma_m^\text{true},例如增/减 10%、20%、50%。
观察并对比蒙特卡洛统计下的滤波表现如何随\sigma_m^\text{filt} 偏离真实值而变化。
Singer 模型参数\alpha 的错误估计:
在仿真中,真实模型使用\alpha^\text{true},但滤波器中使用\alpha^\text{filt} \neq \alpha^\text{true}。
\alpha 决定了加速度自相关的指数衰减速率,若估计不准,滤波器对目标运动的动力学特性理解将产生偏差。
观察卡尔曼滤波器的位置跟踪性能(均方根误差)如何随\alpha^\text{filt} 的改变而波动。
非标称情况一:模型噪声协方差矩阵选择错误
首先,当 真实\sigma_m^\text{true} 与 滤波器\sigma_m^\text{filt} 不同时,滤波器中的过程噪声协方差Q 将与真实轨迹生成时的Q_\text{true} 存在偏差。我们通过多次蒙特卡洛实验,对滤波器性能进行均方根误差(RMSE)评估。
以下示例代码中,我们做了 6 种情况(高估和低估分别 10%、20%、50%),并在图中对比了 测量值 与 卡尔曼滤波估计 两种 RMSE 曲线。示意代码如下:
%% 3.3 第3步:卡尔曼滤波(非标称情况)
% 非标称情况1:模型噪声方差sigma_m选取错误
% 假设真实sigma_m=1,但卡尔曼滤波中使用的sigma_m_filt与真实不一致
% 增大或减小10%、20%、50%
N_BMC = 50; % 蒙特卡罗次数
scaling_factors = [1.1, 0.9; 1.2, 0.8; 1.5, 0.5];
% 行表示不同程度误差,列为高估和低估情况
alpha_true = 1; % 真实轨迹的alpha参数
sigma_m_true = 1; % 真实轨迹的sigma_m
T = 1;
total_time = 500;
num_steps = total_time / T;
sigma_r = 50; % 测量噪声标准差
nx = 3;
nz = 1;
x0 = [0;0;0];
P0 = 1e4*eye(nx);
H = [1 0 0];
R = sigma_r^2;
figure;
sgtitle('非标称情况:模型噪声方差选择错误对卡尔曼滤波性能的影响');
for sf_idx = 1:size(scaling_factors,1)
for col = 1:2
sigma_scale = scaling_factors(sf_idx, col);
sigma_m_filt = sigma_m_true * sigma_scale; % 滤波器中使用的错误sigma_m
% 重新计算滤波用的Phi和Q
Phi_filt = compute_phi(alpha_true, T);
Q_filt = compute_Q(alpha_true, T, sigma_m_filt);
REQM_mesure = zeros(num_steps,1);
REQM_kalman = zeros(num_steps,1);
for iMC = 1:N_BMC
% 真实轨迹(使用真实sigma_m_true)
Phi_true = compute_phi(alpha_true, T);
Q_true = compute_Q(alpha_true, T, sigma_m_true);
[pos_i,~,~] = generate_singer_trajectory(alpha_true, T, num_steps, Phi_true, Q_true, sigma_m_true);
x_true_i = pos_i(1,:,1);
x_meas_i = x_true_i + sigma_r*randn(size(x_true_i));
x_hat_i = zeros(nx, num_steps);
P_hat_i = zeros(nx, nx, num_steps);
x_hat_i(:,1) = x0;
P_hat_i(:,:,1) = P0;
for k = 2:num_steps
x_pred_i = Phi_filt * x_hat_i(:,k-1);
P_pred_i = Phi_filt * P_hat_i(:,:,k-1) * Phi_filt' + Q_filt;
z_k_i = x_meas_i(k);
S_i = H * P_pred_i * H' + R;
K_i = P_pred_i * H' / S_i;
x_hat_i(:,k) = x_pred_i + K_i*(z_k_i - H*x_pred_i);
P_hat_i(:,:,k) = (eye(nx)-K_i*H)*P_pred_i;
end
x_est_i = x_hat_i(1,:);
for n = 1:num_steps
X_verite = x_true_i(n);
X_mesure = x_meas_i(n);
X_kalman = x_est_i(n);
REQM_mesure(n) = REQM_mesure(n) + (X_mesure - X_verite)^2;
REQM_kalman(n) = REQM_kalman(n) + (X_kalman - X_verite)^2;
end
end
REQM_mesure = sqrt(REQM_mesure / N_BMC);
REQM_kalman = sqrt(REQM_kalman / N_BMC);
subplot_idx = (sf_idx-1)*2 + col;
subplot(size(scaling_factors,1),2,subplot_idx); hold on; grid on;
plot(1:num_steps, REQM_mesure, 'r', 'DisplayName', 'REQM_{mesure}');
plot(1:num_steps, REQM_kalman, 'b', 'DisplayName', 'REQM_{kalman}');
xlabel('时间步');
ylabel('REQM');
title(sprintf('sigma_m误差=%.0f%% (滤波使用%.2f, 真值%.2f)', (sigma_scale-1)*100, sigma_m_filt, sigma_m_true));
legend;
end
end
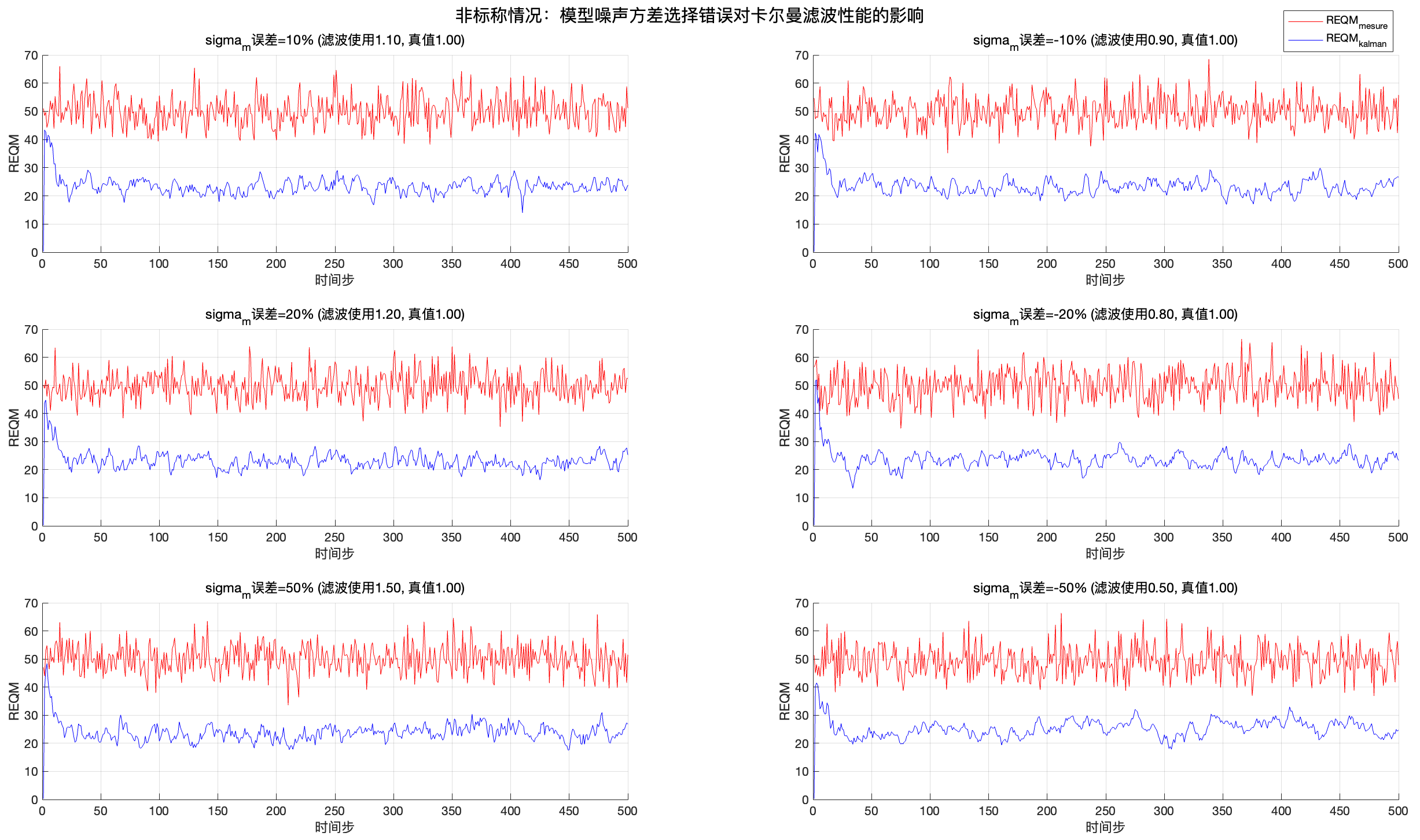
\sigma_m 被低估:卡尔曼滤波器会过分相信“系统模型”而忽略过程噪声的可能性,导致对系统状态变化的灵活度不足,可能出现 慢速响应或状态估计发散。
\sigma_m 被高估:滤波器会过分依赖测量,尽管能在某些时刻更好地更新状态,但容易对测量噪声波动过敏,或在某些时刻产生 瞬时跳动 的情况。
非标称情况二: α 值不同
现在,我们假设滤波器所用的 Singer 模型参数\alpha^\text{filt} 与真实运动中使用的\alpha^\text{true} 不同。这意味着卡尔曼滤波器对 加速度自相关 的时间常数估计出现偏差,从而在状态转移矩阵和过程噪声协方差的构造上都产生了 不匹配。
以下代码给出了不同\alpha^\text{filt} 相对于真实\alpha^\text{true}=1 的情况(如 0.5、1、2)时的效果比较:
%% 非标称情况2:alpha值不同
% 假设真实alpha为1,但滤波时使用不同的alpha_filt来构造Phi_filt和Q_filt。
alpha_values = [0.5, 1, 2]; % 使用比真实值偏差的alpha进行滤波
figure;
sgtitle('非标称情况:alpha值与真实不匹配对卡尔曼滤波性能的影响');
for a_idx = 1:length(alpha_values)
alpha_filt = alpha_values(a_idx);
REQM_mesure = zeros(num_steps,1);
REQM_kalman = zeros(num_steps,1);
for iMC = 1:N_BMC
% 真实轨迹
Phi_true = compute_phi(alpha_true, T);
Q_true = compute_Q(alpha_true, T, sigma_m_true);
[pos_i,~,~] = generate_singer_trajectory(alpha_true, T, num_steps, Phi_true, Q_true, sigma_m_true);
x_true_i = pos_i(1,:,1);
x_meas_i = x_true_i + sigma_r*randn(size(x_true_i));
% 非标称滤波器 (使用错的alpha_filt)
Phi_filt = compute_phi(alpha_filt, T);
Q_filt = compute_Q(alpha_filt, T, sigma_m_true); % 假设sigma_m不变,仅alpha错
x_hat_i = zeros(nx, num_steps);
P_hat_i = zeros(nx, nx, num_steps);
x_hat_i(:,1) = x0;
P_hat_i(:,:,1) = P0;
for k = 2:num_steps
x_pred_i = Phi_filt * x_hat_i(:,k-1);
P_pred_i = Phi_filt * P_hat_i(:,:,k-1) * Phi_filt' + Q_filt;
z_k_i = x_meas_i(k);
S_i = H * P_pred_i * H' + R;
K_i = P_pred_i * H' / S_i;
x_hat_i(:,k) = x_pred_i + K_i*(z_k_i - H*x_pred_i);
P_hat_i(:,:,k) = (eye(nx)-K_i*H)*P_pred_i;
end
x_est_i = x_hat_i(1,:);
for n = 1:num_steps
X_verite = x_true_i(n);
X_mesure = x_meas_i(n);
X_kalman = x_est_i(n);
REQM_mesure(n) = REQM_mesure(n) + (X_mesure - X_verite)^2;
REQM_kalman(n) = REQM_kalman(n) + (X_kalman - X_verite)^2;
end
end
REQM_mesure = sqrt(REQM_mesure / N_BMC);
REQM_kalman = sqrt(REQM_kalman / N_BMC);
subplot(length(alpha_values),1,a_idx); hold on; grid on;
plot(1:num_steps, REQM_mesure, 'r', 'DisplayName', 'REQM_{mesure}');
plot(1:num_steps, REQM_kalman, 'b', 'DisplayName', 'REQM_{kalman}');
xlabel('时间步');
ylabel('REQM');
title(sprintf('滤波器使用alpha=%.2f, 真值alpha=%.2f', alpha_filt, alpha_true));
legend;
end
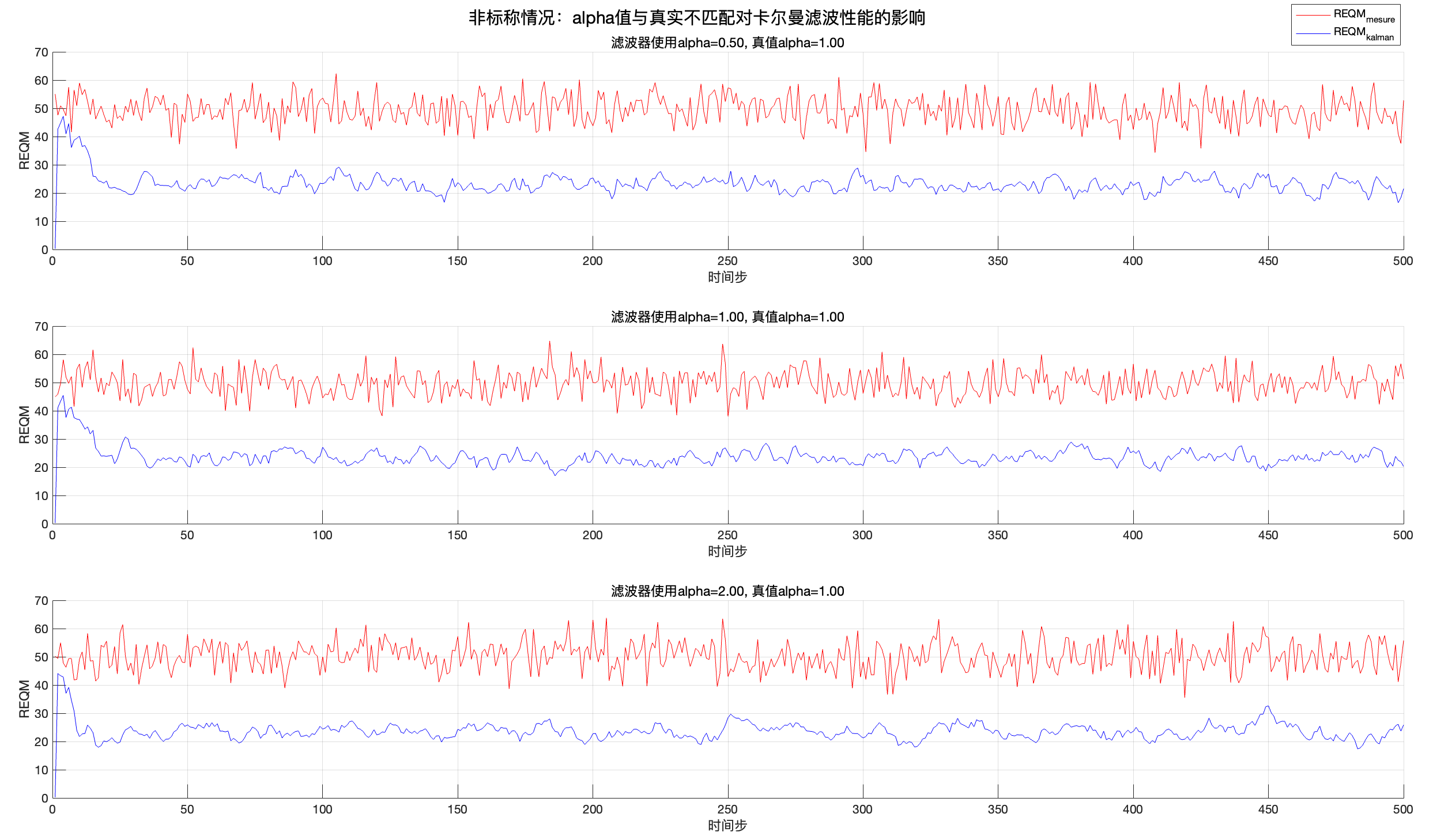
\alpha 被低估:若滤波器认为加速度相关性衰减过快,可能在对系统加速度的“平滑性”上信任不足,某些情况下会更容易受到噪声扰动影响。
\alpha 被高估:若滤波器认为加速度相关性衰减过慢,则会过于“惯性”地维持原有状态,可能导致对实际快速变化的响应滞后或估计不准
在“非标称”条件下,卡尔曼滤波器针对目标运动的假设与真实情况不完全一致。通过数值实验可以看出:
过程噪声方差\sigma_m 不匹配 会导致滤波器对测量和模型的信赖程度出现偏差,从而影响稳态误差与瞬态响应。
\alpha 不匹配 意味着对加速度自相关特征的错误建模,也会带来滤波精度的下降。