zehua

Zehua

应用随机梯度算法解决信道均衡问题

信号处理
31
0
2024-06-08

背景介绍

我们目标是利用优化算法并构建滤波器来解决信号通道的失真（噪声、多径传播）等问题。

具体思路步骤如下:

我们有一个原始信号 s(n) ，经过传输信道后可用如下数学模型描述:

x(n)=s(n)*h(n)+u(n)

这里， w(n) 表示信道的冲激响应（相当于滤波器），而 u(n) 表示加性噪声。

这是个非常经典的卷积加噪模型公式，但是这里我们有一个不同之处是，我们并不知道信道的冲击响应 w(n) 或频率响应 W(f) ，因此我们首先需要估计这个 \hat{w}(n) ，这一步叫做 估计信道。所以我们先发送一个预先已知的训练序列 s_{\text{train}}(n) 进入信道中，因此接收端信号如下：

x_{\text{train}}(n)=s_{\text{train}}(n)*h(n)+w(n)

利用 s_{\text{train}}(n) 与 x_{\text{train}}(n) 之间的关系，可以采用不同的算法（如最小均方误差）来估计出信道的冲激响应 \hat{w}(n) 。

这一步并不是我们的核心，我们需要解决的问题是信号在经过信道后的失真问题，也就是我们得到的 x(n) 失真，所以一般思路即是在 x(n) 后面搭一个均衡滤波器 g(n) ，我们要逆转信道对信号的影响，滤波后的信号记做 \hat{s}(n) :

\hat{s}(n)=x(n)*g(n)

如果纯理想情况下，信道无噪且可逆，那么我们有:

g(n)=1/h(n)

那就是纯理论反卷积，当然我们知道这是不可能实现的，不然就没有这么多反卷积方法了，这里我们选择的反卷积方法是 自适应滤波器，这是有讲究的，因为原始通道 w(n) 并不是固定的，是可能随时间变化的，导致原本构建好的 g(n) 滤波器系数就无法补偿当前的信号失真，因此我们的想法是 g(n) 为自适应滤波， w(n) 变我就变，这样滤波器就可以跟踪信道变化了。

因此自适应滤波器 g(n) 的输出 \hat{s}(n) 应该尽可能接近原始信号 s(n) ，这就需要一个评判标准，就最小均方误差 LMS 算法

\min_{g(n)}E\{|e(n)|^2\}

  • 其中 e(n)=s(n)-\hat{s}(n)

随迭代不断更新均衡滤波器 g(n) 的参数序列，因此我们可以把优化问题看作成一个自适应滤波任务

这里的LMS 算法是一种随机梯度下降算法，其核心思想是当前样本估计全局梯度。它利用每个时刻的瞬时误差 e(n) 来估计均方误差 E\{|e(n)|^2\} 关于滤波器系数 g(n) 的梯度，然后根据该近似梯度更新 g(n) 的值，以逐步减小误差。其具体步骤如下:

在 LMS 算法中，我们希望最小化均方误差

J=E\{e(n)^2\}=E\{(s(n)-\hat{s}(n))^2\}

其中，滤波器的输出

\hat{s}(n)=\sum_{j=0}^{M-1}g_j\,x(n-j)

因此，误差可以写为

e(n)=s(n)-\sum_{j=0}^{M-1}g_j\,x(n-j)

对 J 关于滤波器系数 g_k 求偏导，我们有

\frac{\partial J}{\partial g_k}=\frac{\partial}{\partial g_k}E\{e(n)^2\}=E\left\{\frac{\partial e(n)^2}{\partial g_k}\right\}

期望运算是线性的，可以把求导运算移到期望内部。

利用链式法则对 e(n)^2 求导，得到

\frac{\partial e(n)^2}{\partial g_k}=2\,e(n)\,\frac{\partial e(n)}{\partial g_k}

注意到 s(n) 与 g_k 无关，而求和项中只有当 j=k 的项与 g_k 有关，所以有

\frac{\partial e(n)}{\partial g_k}=\frac{\partial}{\partial g_k}\left(s(n)-\sum_{j=0}^{M-1}g_j\,x(n-j)\right) =-x(n-k)

将上式代入链式法则中

\frac{\partial e(n)^2}{\partial g_k}=2\,e(n)\,(-y(n-k))=-2\,e(n)x(n-k)

最后，将其代入成本函数的梯度表达式中

\frac{\partial J}{\partial g_k}=E\{-2\,e(n)y(n-k)\}=-2\,E\{e(n)x(n-k)\}

但由于直接计算 E\{e(n)x(n-k)\} 需要整个数据分布的信息，而在实时应用中往往无法获得这种全局统计数据，LMS 算法便采用了 随机梯度下降 的方法，即用当前时刻的样本 e(n)x(n-k) 来近似那个期望。这样，当前时刻估计的梯度为

\hat{\nabla}_{g_k}J=-2e(n)x(n-k)

随后，滤波器系数按照负梯度方向更新，更新公式为

g_k(n+1)=g_k(n)+\mu\, e(n)x(n-k)

  • 步长参数 \mu 把那个系数 2 包住了

由于每个更新步骤中的梯度都是基于随机采样的结果，因此更新过程中带有噪声，具有随机性。这种方法在实时自适应滤波器设计中非常实用，因为它计算量小且能追踪信道的变化。


 

传输链路的建模与仿真

w(k) = \begin{cases} \frac{1}{2} \left( 1 + \cos\left(\frac{2\pi}{\beta}(k - 1)\right) \right), & \text{for } k = 0, 1, 2, \\ 0, & \text{else} \end{cases}

 此外，接收信号受到加性高斯噪声u(n) 的干扰，加性高斯噪声具有白噪音的特性（独立同分布），零均值，方差为\sigma^2 = 0.001。

因此，信号的表达式为： 

x(n) = \sum_{k=0}^{2} w(k)s(n-k) + u(n)

 其中，\beta 控制信道引入的失真水平。

我们先在 Matlab 中使用函数stem 生成由符号1 和-1 组成的随机序列信号s(n)，并假设1 和-1 取值是等概率的。我们可以使用函数randn，并假设信号的长度为N = 1500。

clear all
clc
close all

% 参数设置
N = 1500;

% 生成随机信号 s(n) 为 +1 或 -1
s = sign(randn(N,1));

% 绘制离散信号 s(n)
figure;
stem(s); % 离散信号绘图
title('信号 s(n)', 'FontSize', 16);
xlabel('信号长度 N', 'FontSize', 14);
ylabel('s(n)', 'FontSize', 14);
set(gca, 'FontSize', 12); % 放大坐标轴刻度

只展示了 200 的序列

由于信号s(n) 是由符号1 和-1 组成的随机序列，且被假设等概率的: X = {+1, -1} p_{+1} = p_{-1} = \frac{1}{2}

 因此， s(n) 的期望形式为：

E[s(n)] = p_{+1} \cdot (+1) + p_{-1} \cdot (-1)
E[s(n)] = \frac{1}{2} \cdot (+1) + \frac{1}{2} \cdot (-1)
E[s(n)] = 0

 我们接下来绘制传播信道，其公式为:

w(k) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{\beta}(k - 1) \right) \right)

 对\beta 取不同值：0.25,2 和4 来进行观察

  • 对于\beta = 0.25 ：

当\beta 较小时，例如0.25，传输信道具有较短的脉冲响应，这会导致余弦函数的快速变化。在这种情况下，可以预期w(k) 在k = 0 到k = 2 之间有显著变化。

w(0) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{0.25}(-1) \right) \right) = \frac{1}{2} \left( 1 + \cos(-8\pi) \right) = \frac{1}{2}(1 + 1) = 1
w(1) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{0.25}(0) \right) \right) = \frac{1}{2} \left( 1 + \cos(0) \right) = \frac{1}{2}(1 + 1) = 1
w(2) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{0.25}(1) \right) \right) = \frac{1}{2} \left( 1 + \cos(8\pi) \right) = \frac{1}{2}(1 + 1) = 1

 因此，当\beta = 0.25 时， w(k) 在点k = 0, 1, 2 处的值均为1。

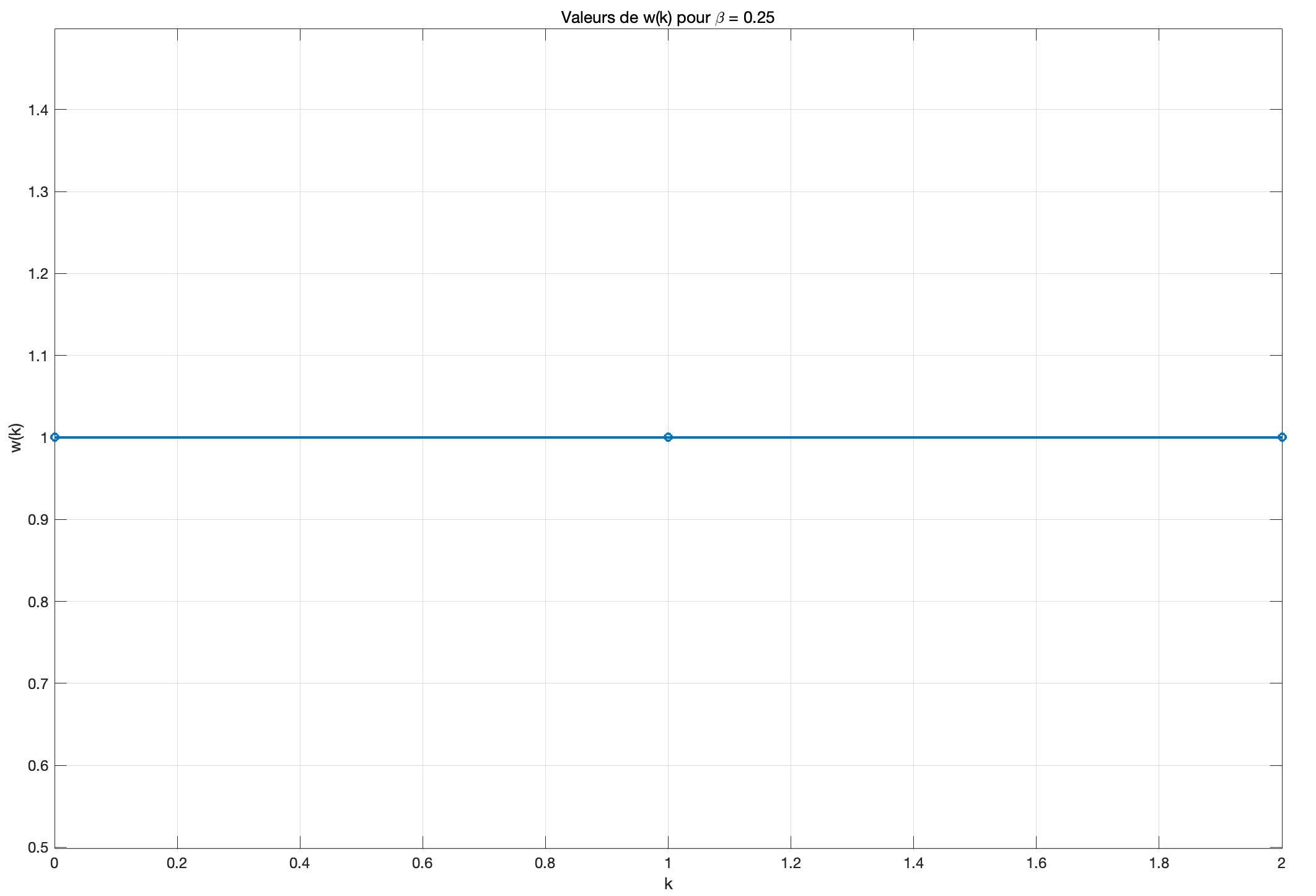
可以看到传播信道在前3 个采样点上具有恒定的脉冲响应。

  • 对于\beta = 2 ：

w(0) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{2}(-1) \right) \right) = \frac{1}{2} \left( 1 + \cos(-\pi) \right) = \frac{1}{2}(1 - 1) = 0
w(1) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{2}(0) \right) \right) = \frac{1}{2} \left( 1 + \cos(0) \right) = \frac{1}{2}(1 + 1) = 1
w(2) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{2}(1) \right) \right) = \frac{1}{2} \left( 1 + \cos(\pi) \right) = \frac{1}{2}(1 - 1) = 0

因此，对于\beta = 2， w(k) 在点k = 0 和k = 2 的值为0，而在点k = 1 的值为1。

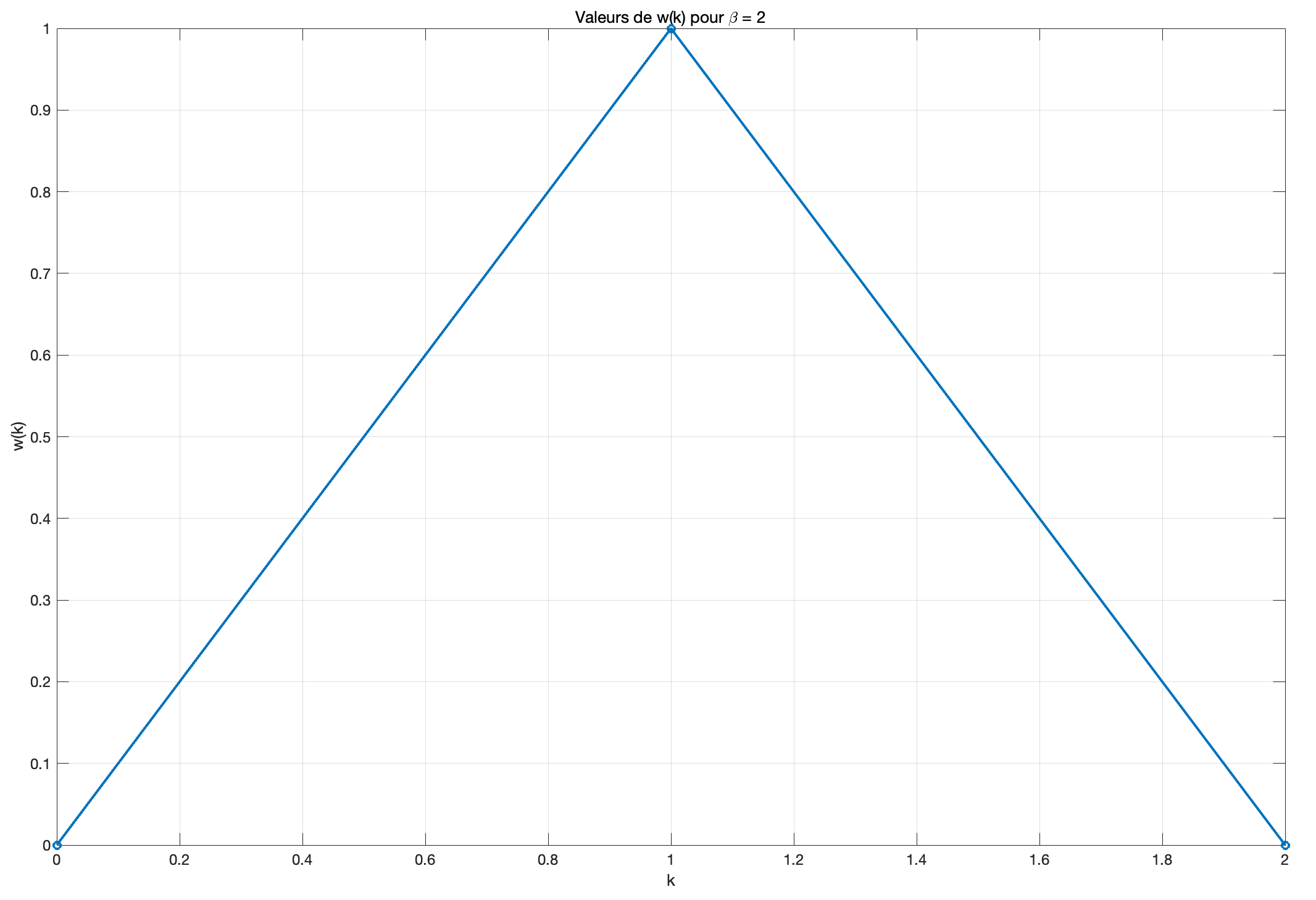
可以看到传播信道的脉冲响应主要集中在k = 1，主要影响第一个延迟的信号。

  • 对于\beta = 4 ：

当\beta 更大时，例如4，传输信道的脉冲响应周期进一步延长，余弦函数的变化变得更慢。在这种情况下，可以预期w(k) 在k = 0 到k = 2 之间的变化较小。

w(0) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{4}(-1) \right) \right) = \frac{1}{2} \left( 1 + \cos\left(-\frac{\pi}{2}\right) \right) = \frac{1}{2}(1 + 0) = \frac{1}{2}
w(1) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{4}(0) \right) \right) = \frac{1}{2} \left( 1 + \cos(0) \right) = \frac{1}{2}(1 + 1) = 1
w(2) = \frac{1}{2} \left( 1 + \cos \left( \frac{2\pi}{4}(1) \right) \right) = \frac{1}{2} \left( 1 + \cos\left(\frac{\pi}{2}\right) \right) = \frac{1}{2}(1 + 0) = \frac{1}{2}

因此，对于\beta = 4， w(k) 在点k = 0 和k = 2 的值为0.5，而在点k = 1 的值为1。

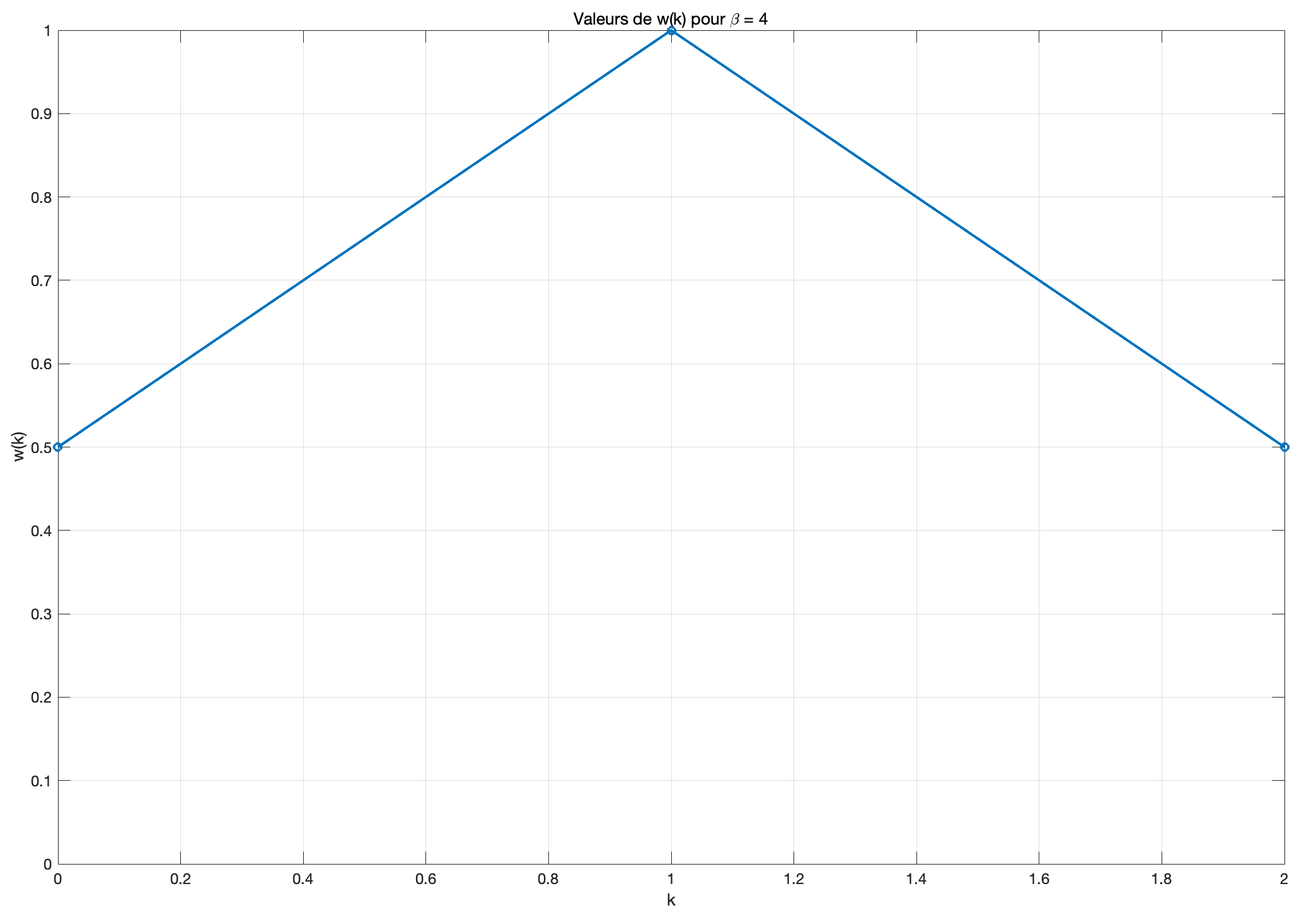
可以看到传播信道具有一个对称的脉冲响应，其峰值位于k = 1，如\beta = 2 的情况（图 3），但它在第一个和第三个采样点上也包含非零值。即脉冲响应更加分散且对称，但主要集中在中心。

这表明，具有均匀或扩展脉冲响应的信道需要均衡器来补偿分布在多个采样点上的失真；而具有集中脉冲响应的信道可能更容易均衡，因为失真主要局限于单个采样点。

后续中，我们将使用\beta = 0.25，通过已经构建好的随机序列信号s(n)，使用 Matlab 函数filter 来添加加性噪声，以获得信号x(n)。

%% 给信号加噪音
% 滤波器脉冲响应（权值）
w = [1 1 1];

% 对 s(n) 进行滤波
% filter(num, den, data_to_filter)
x = filter(w, 1, s);

sigma_u = sqrt(0.001); % 高斯噪声标准差

% 向滤波后的信号中加入高斯噪声
u = sigma_u * randn(N,1);
x = x + u;

% 绘制加入噪声后的信号 x(n)
figure;
stem(x);
title('信号 x(n)', 'FontSize', 16);
xlabel('信号长度 N', 'FontSize', 14);
ylabel('x(n)', 'FontSize', 14);
set(gca, 'FontSize', 12); % 放大坐标轴刻度

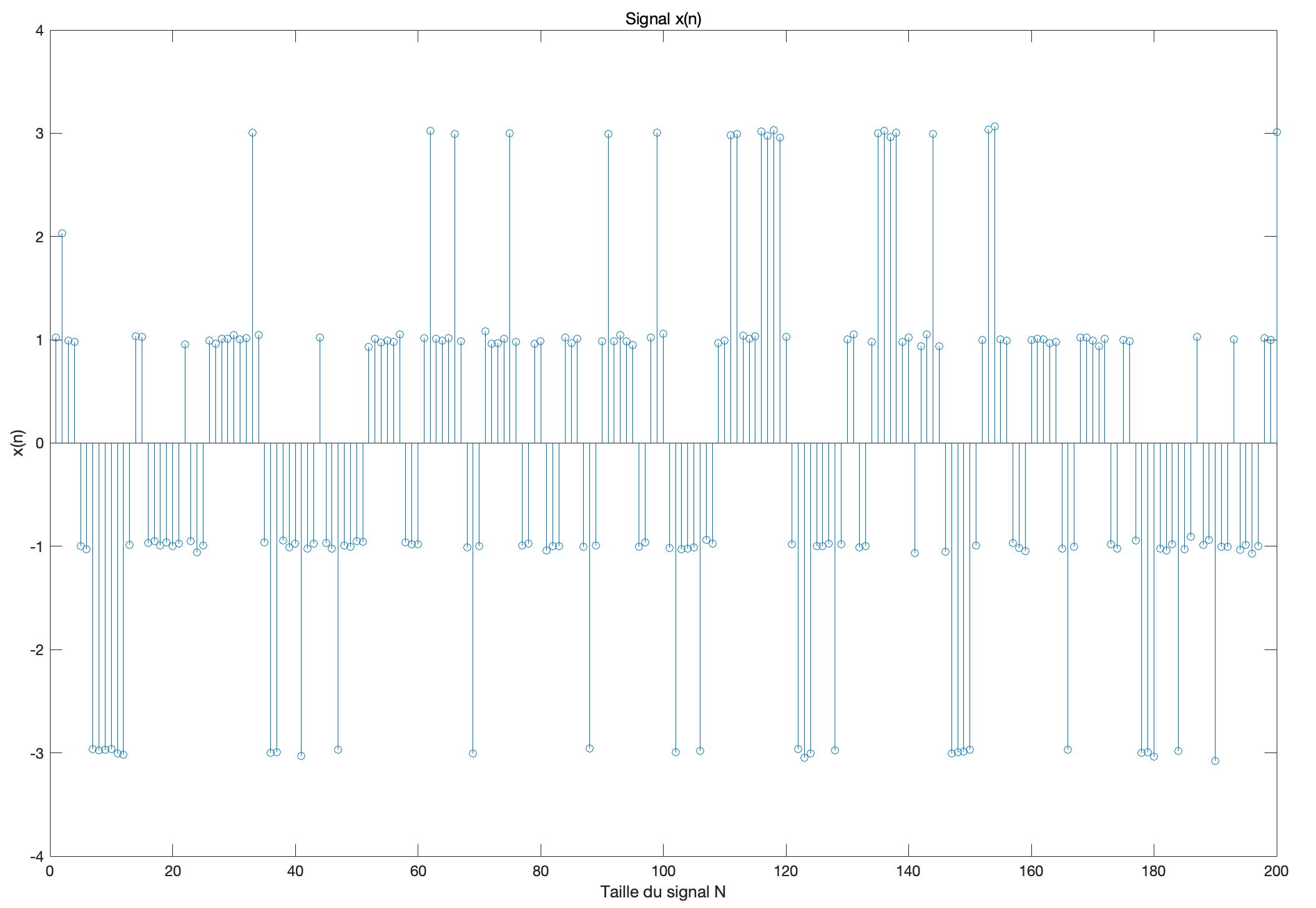
实现均衡

 为了实现信道均衡，我们最终目标是确定最优维纳滤波器h_{\text{opt}} 的理论表达式，以最小化均方误差。为此，首先需要计算信号x(n) 的自相关函数和x(n) 与d(n) 的互相关函数，分别记为r_{xx}(k) 和r_{dx}(k)。对于真实且平稳的信号，其相关函数公式为：

r_{xx}(k) = E[x(n)x(n-k)]
r_{dx}(k) = E[d(n)x(n-k)]

我们首先研究（由传播信道卷积得到的）发射信号m(n) 的自相关函数r_{mm}(k)，其中m(n) = \sum_{k=0}^{2} w(k)s(n-k)。首先计算r_{mm}(0)、r_{mm}(1) 和r_{mm}(2) 来观察结果。同时注意，我们之前假设符号s(n) 为相互独立的。

补充: 这里的 d(n) 是 s(n) 的时间延时，具体为:

d(n) \;=\; s(n - 2)

  • 如果我们不对齐延迟，直接拿 s(n) 当目标信号，那么信道会导致延迟，导致滤波器输出 \hat{s}(n) 在时间上无法和 s(n) 对齐，计算出来的误差会乱套，也就无法用来更新滤波器。通过令 d(n) = s(n-2)，我们就补偿了这个延迟。

计算 rmm(0)

r_{mm}(0) = E \left[ \left( \sum_{k=0}^{2} w(k)s(n-k) \right)^2 \right]
r_{mm}(0) = \sum_{k=0}^{2} w^2(k) E[s^2(n-k)]

由于s(n) 是相互独立的，因此有：

E[s^2(n-k)] = 1

 由于s(n) 的特性：

E[s^2(n)] = 1 \cdot P(s(n) = 1) + 1 \cdot P(s(n) = -1)
E[s^2(n)] = 1 \cdot \frac{1}{2} + 1 \cdot \frac{1}{2} = 1

因此：

 

r_{mm}(0) = \sum_{k=0}^{2} w^2(k)
r_{mm}(0) = w(0)^2 + w(1)^2 + w(2)^2 = 3

计算 rmm(1)

r_{mm}(1) = E[m(n)m(n-1)]
r_{mm}(1) = E \left[ \left( \sum_{k=0}^{2} w(k)s(n-k) \right) \left( \sum_{j=0}^{2} w(j)s(n-1-j) \right) \right]
r_{mm}(1) = \sum_{k=0}^{2} \sum_{j=0}^{2} w(k)w(j) E[s(n-k)s(n-1-j)]

同样，仅当k = j + 1 时，相关函数才不为零，因此：

r_{mm}(1) = w(0)w(1)E[s(n-1)s(n-1)] + w(1)w(2)E[s(n-2)s(n-2)]

由于E[s(n)] = 0，因此：

E[s^2(n)] = 1

因此：

r_{mm}(1) = w(0)w(1) \cdot 1 + w(1)w(2) \cdot 1
r_{mm}(1) = w(0)w(1) + w(1)w(2) = 2

计算 rmm(2)

r_{mm}(2) = E \left[ \left( \sum_{k=0}^{2} w(k)s(n-k) \right) \left( \sum_{j=0}^{2} w(j)s(n-2-j) \right) \right]
r_{mm}(2) = \sum_{k=0}^{2} \sum_{j=0}^{2} w(k)w(j) E[s(n-k)s(n-2-j)]

同样，仅当k = j + 2 时，相关函数才不为零，因此：

r_{mm}(2) = w(0)w(2)E[s(n-2)s(n-2)]

由于E[s(n)] = 0，因此：

E[s^2(n-2)] = 1

因此：

r_{mm}(2) = w(0)w(2) = 1

接下来我们需要找到当k > 2 时， r_{mm}(k) = 0 并推出任意k 时r_{mm}(k) 的表达式。

为了验证r_{mm}(k) = 0 当k > 2，我们先计算r_{mm}(3) 看看：

r_{mm}(3) = E \left[ \left( \sum_{k=0}^{2} w(k)s(n-k) \right) \left( \sum_{j=0}^{2} w(j)s(n-3-j) \right) \right]
r_{mm}(3) = \sum_{k=0}^{2} \sum_{j=0}^{2} w(k)w(j) E[s(n-k)s(n-3-j)]

同样，仅当k = j + 3 时，相关函数才不为零，因此：

r_{mm}(3) = w(0)w(3)E[s(n-3)s(n-3)]

由于：

w(k) = 0 , \text{对于 } k \neq 0, 1, 2

因此：

w(3) = 0

因此：

r_{mm}(3) = 0

结论

r_{mm}(k) = \begin{cases} w(0)^2 + w(1)^2 + w(2)^2 & \text{当 } k = 0 \\ w(0)w(1) + w(1)w(2) & \text{当 } k = 1 \\ w(0)w(2) & \text{当 } k = 2 \\ 0 & \text{当 } k > 2 \end{cases}
r_{mm}(k) = \begin{cases} 3 & \text{当 } k = 0 \\ 2 & \text{当 } k = 1 \\ 1 & \text{当 } k = 2 \\ 0 & \text{当 } k > 2 \end{cases}

计算 rxx(k)

我们使用已经得到的结果来计算r_{xx}(k)

我们已知x(n) = m(n) + u(n)，并且噪声u(n) 被假设为独立于传输符号的。

r_{xx}(k) = E[x(n)x(n-k)]
r_{xx}(k) = E\left[(m(n) + u(n))(m(n-k) + u(n-k))\right]
r_{xx}(k) = E[m(n)m(n-k)] + E[m(n)u(n-k)] + E[u(n)m(n-k)] + E[u(n)u(n-k)]

由于m(n) 和u(n) 是独立的：

E[m(n)u(n-k)] = 0

并且u(n) 是零均值的白噪声：

E[u(n)u(n-k)] = \sigma_u^2\delta(k)

因此：

r_{xx}(k) = r_{mm}(k) + \sigma_u^2\delta(k)
r_{xx}(k) = \begin{cases} w(0)^2 + w(1)^2 + w(2)^2 + \sigma_u^2 & \text{当 } k = 0 \\ w(0)w(1) + w(1)w(2) & \text{当 } k = 1 \\ w(0)w(2) & \text{当 } k = 2 \\ 0 & \text{当 } k > 2 \end{cases}
r_{xx}(k) = \begin{cases} 3 + \sigma_u^2 & \text{当 } k = 0 \\ 2 & \text{当 } k = 1 \\ 1 & \text{当 } k = 2 \\ 0 & \text{当 } k > 2 \end{cases}

hopt 的表达式

最终我们计算r_{dx}(k) 并最终给出h_{\text{opt}} 的表达式。

r_{dx}(k) = E[d(n)x(n-k)]

已知d(n) = s(n-2) 且x(n) = m(n) + u(n)：

r_{dx}(k) = E[s(n-2)(m(n-k) + u(n-k))]

由于u(n) 和s(n) 是独立的且u(n) 的均值为0:

E[s(n-2)u(n-k)] = 0

因此 :

r_{dx}(k) = E[s(n-2)m(n-k)]

由于已知：

m(n) = \sum_{k=0}^{2} w(k)s(n-k)

因此：

r_{dx}(k) = E[s(n-2)(w(0)s(n-k) + w(1)s(n-k-1) + w(2)s(n-k-2))]

当k = 0 时：

r_{dx}(0) = w(2)E[s(n-2)s(n-2)] = w(2)

当k = 1 时: 

r_{dx}(1) = w(1)E[s(n-2)s(n-2)] = w(1)

当k = 2 时：

r_{dx}(2) = w(0)E[s(n-2)s(n-2)] = w(0)

结论

r_{dx}(k) = \begin{cases} w(2) & \text{当 } k = 0 \\ w(1) & \text{当 } k = 1 \\ w(0) & \text{当 } k = 2 \\ 0 & \text{当 } k > 2 \end{cases}

并且：

h_{\text{opt}} = R_{xx}^{-1}r_{dx}
h_{\text{opt}} = \begin{pmatrix} r_{xx}(0) & r_{xx}(1) & r_{xx}(2) \\ r_{xx}(1) & r_{xx}(0) & r_{xx}(1) \\ r_{xx}(2) & r_{xx}(1) & r_{xx}(0) \end{pmatrix}^{-1} \begin{pmatrix} r_{dx}(0) \\ r_{dx}(1) \\ r_{dx}(2) \end{pmatrix}
h_{\text{opt}} = \begin{pmatrix} r_{xx}(0) & r_{xx}(1) & r_{xx}(2) \\ r_{xx}(1) & r_{xx}(0) & r_{xx}(1) \\ r_{xx}(2) & r_{xx}(1) & r_{xx}(0) \end{pmatrix}^{-1} \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}

 

实现

我们将在 Matlab 中设计一个滤波器，并使用两种方法计算自相关和互相关来构建滤波器：一种方法是基于理论公式，用Toeplitz 函数构造自相关矩阵；另一种方法是通过 Matlab 的xcorr 函数以数值方式计算这些相关函数，然后比较两种方法下得到的滤波器结果。

 我们先看第一种实现，使用上述得到的计算公式，并利用Toeplitz 函数构造自相关矩阵。

%% 第一种实现
L = 11;

% 计算自相关函数 r_xx(k)
% r_xx(0)
r_xx1 = w(1)^2 + w(2)^2 + w(3)^2 + sigma_u^2;
% r_xx(1)
r_xx2 = w(1)*w(2) + w(2)*w(3);
% r_xx(2)
r_xx3 = w(1)*w(3);
% 对 k > 2，r_xx(k) = 0
r_xx = [r_xx1; r_xx2; r_xx3; zeros(8,1)];

% 构建 Toeplitz 矩阵 R_xx
R_xx = toeplitz(r_xx);

% 计算互相关函数 r_dx(k)
% r_dx(0)
r_dx1 = w(3);
% r_dx(1)
r_dx2 = w(2);
% r_dx(2)
r_dx3 = w(1);
% 对 k > 2，r_dx(k) = 0
r_dx = [r_dx1; r_dx2; r_dx3; zeros(8,1)];

% 使用 Wiener-Hopf 方程求解最优滤波器系数
h_opt = inv(R_xx)*r_dx;
disp('Wiener 最优滤波器 h_opt:');
disp(h_opt);

第二种实现，通过 Matlab 的xcorr 函数以数值方式（不依赖理论公式，直接应用样本数据）计算这些相关函数

%% 第二种实现
hopt_theo = h_opt;

% 定义 d(n) = s(n-2)
d = s(1:end-2);
x2 = x(3:end);

% 数值计算 r_xx
r_xx_num = xcorr(x2);
r_xx_num = r_xx_num(N-2:N-2+L-1);

% 数值计算 r_dx
r_dx_num = xcorr(d, x2);
r_dx_num = r_dx_num(N-2:N-2+L-1);

% 构建数值 Toeplitz 矩阵 R_xx_num
R_xx_num = toeplitz(r_xx_num);

% 数值求解最优滤波器系数
h_opt_num = inv(R_xx_num)*r_dx_num;

% 绘制理论与数值求解得到的最优滤波器系数
figure,
stem(hopt_theo), title('理论最优滤波器', 'FontSize',16), hold on;
stem(h_opt_num), title('数值最优滤波器', 'FontSize', 16)
xlabel('滤波器阶数 L','FontSize',14),
ylabel('幅度', 'FontSize',14)
set(gca, 'FontSize', 14);
legend('理论结果','数值结果')

 

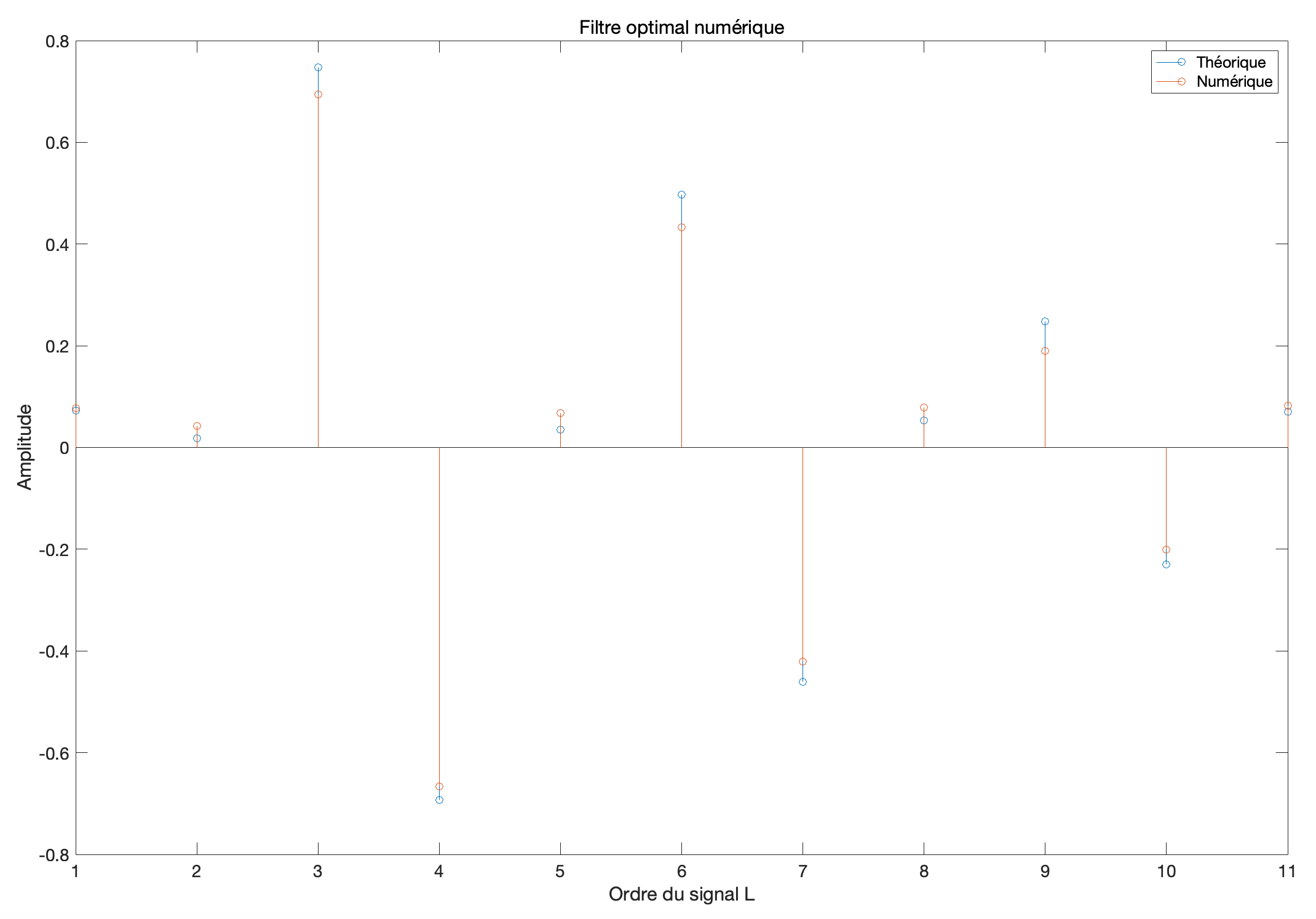
我们发现数值滤波器（Numérique）非常接近理论最优滤波器（Théorique）。

现在，我们应用 LMS 算法来迭代解决信道估计问题，这里假设L = 11。我们创建一个函数algoLMS，该函数接收输入信号x(n) 和d(n)，脉冲响应长度L，以及步长\mu，并输出后验误差序列e^+(n) 和通过 LMS 算法迭代得到的脉冲响应h_n。并通过调整步长\mu 来测试算法，并且展示滤波器系数误差的范数|h_n - h_{\text{opt}}|_2。

%% LMS算法
% 学习步长数组
mu = [0.001, 0.005, 0.01, 0.02];

% 对不同步长 mu 执行 LMS 算法
[err1, h1] = algoLMS(x2, d, L, mu(1));
[err2, h2] = algoLMS(x2, d, L, mu(2));
[err3, h3] = algoLMS(x2, d, L, mu(3));
[err4, h4] = algoLMS(x2, d, L, mu(4));

% 计算滤波器系数误差的范数
normeh1 = sqrt(sum((h1 - hopt_theo).^2));
normeh2 = sqrt(sum((h2 - hopt_theo).^2));
normeh3 = sqrt(sum((h3 - hopt_theo).^2));
normeh4 = sqrt(sum((h4 - h_opt).^2, 1));

% 绘制后验误差 e+(n) 随 n 的变化
% 使用子图分别展示不同 μ 值下的后验误差，以获得更清晰的对比

figure;

% μ = 0.001
subplot(2,2,1);
plot(err1); grid on;
xlabel('信号长度 N', 'FontSize', 14);
ylabel('e(n)', 'FontSize', 14);
title('μ = 0.001', 'FontSize', 14);

% μ = 0.005
subplot(2,2,2);
plot(err2); grid on;
xlabel('信号长度 N', 'FontSize', 14);
ylabel('e(n)', 'FontSize', 14);
title('μ = 0.005', 'FontSize', 14);

% μ = 0.01
subplot(2,2,3);
plot(err3); grid on;
xlabel('信号长度 N', 'FontSize', 14);
ylabel('e(n)', 'FontSize', 14);
title('μ = 0.01', 'FontSize', 14);

% μ = 0.02
subplot(2,2,4);
plot(err4); grid on;
xlabel('信号长度 N', 'FontSize', 14);
ylabel('e(n)', 'FontSize', 14);
title('μ = 0.02', 'FontSize', 14);


% 绘制与 h_opt 的误差范数随 n 的变化
figure;
plot(normeh1); grid on; hold on;
plot(normeh2);
plot(normeh3);
plot(normeh4);
xlabel('信号长度 N', 'FontSize', 14);
ylabel('||h(n)-h_{opt}||^2', 'FontSize', 14);
title('后验误差范数', 'Interpreter', 'none', 'FontSize', 16);
legend('\mu = 0.001', '\mu = 0.005', '\mu = 0.01', '\mu = 0.02');

子函数:

function [eplus,h_tout] = algoLMS(x,d,L,mu)
% 实现 LMS 算法的函数

N = length(x);
h = ones(L,1);
eplus = zeros(N,1);
h_tout = zeros(L,N);

for n = L:N
    xn = x(n:-1:n-L+1);
    yn = h'*xn;
    eplus(n) = d(n) - yn;
    % LMS 更新方程
    h = h + mu*xn*(d(n)-xn'*h);
    h_tout(:,n) = h;
end

end

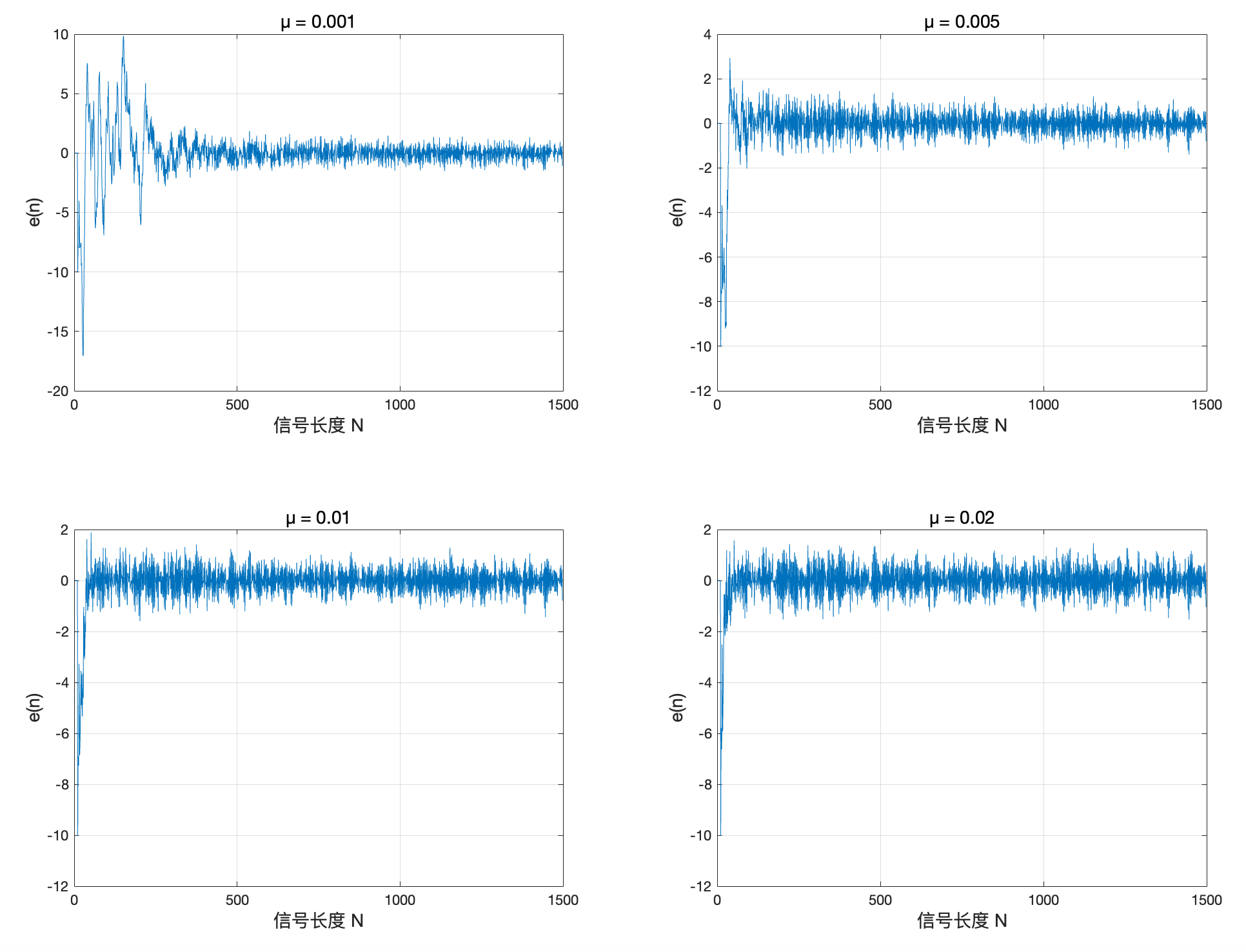
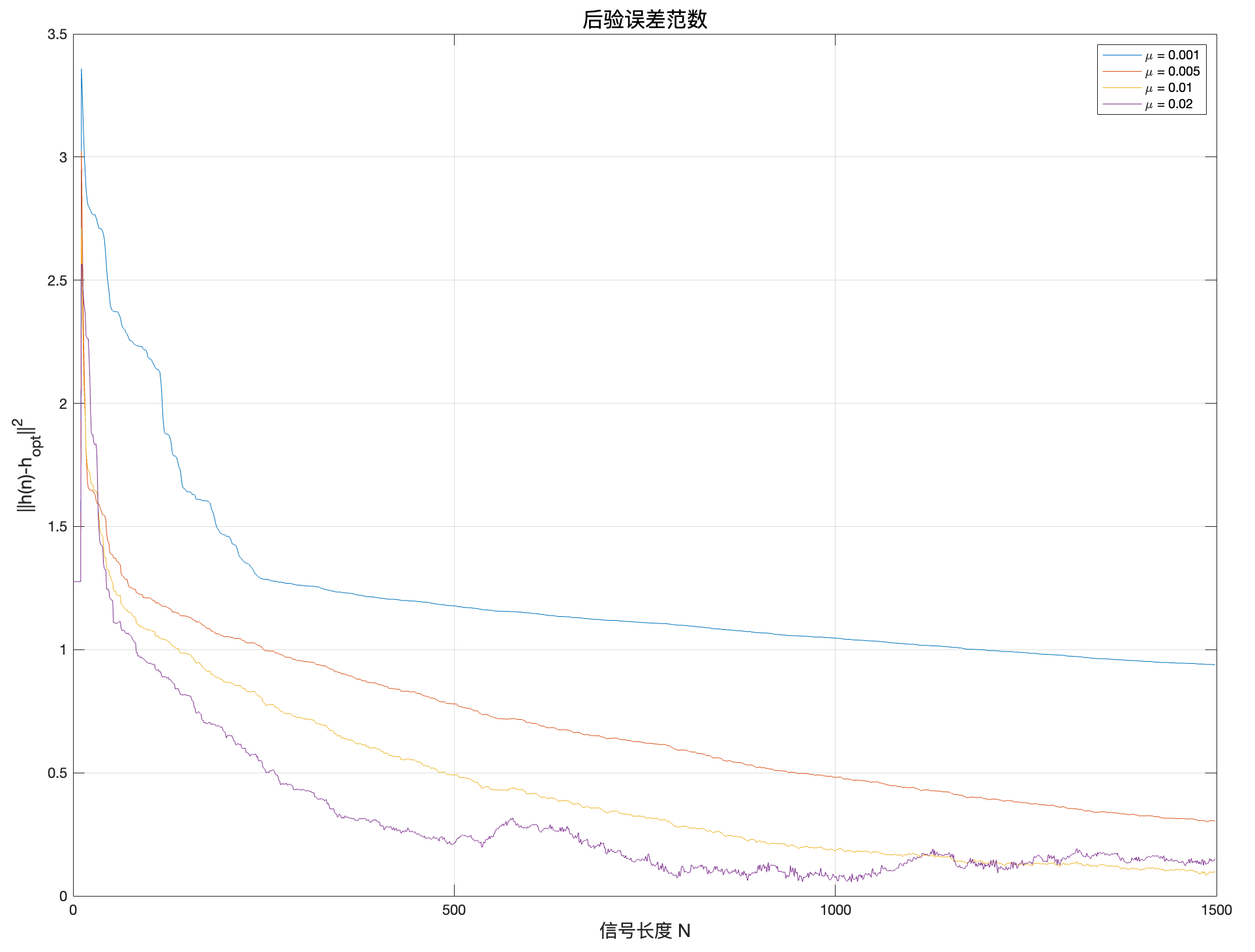
我们下面计算理论上使算法收敛的步长\mu 的最大值，并和实际值做对比。

 收敛的充分必要条件为：

0 < \mu < \frac{2}{\lambda_{\text{max}}}

  • 其中，\lambda_{\text{max}} 是自相关矩阵R_{xx} 的最大特征值。

证明

1. 期望意义下的迭代公式

LMS 算法的更新公式为：

h_n = h_{n-1} + \mu\,x(n)\,\bigl(d(n) - x(n)^T h_{n-1}\bigr)

在期望意义下取数学期望E[\cdot]，得到：

E[h_n] = E[h_{n-1}] + \mu\,E\Bigl[x(n)\bigl(d(n) - x(n)^T h_{n-1}\bigr)\Bigr]

拆开后可得：

E[h_n] = E[h_{n-1}] + \mu \bigl( E[x(n) d(n)] - E[x(n) x(n)^T h_{n-1}] \bigr)

通常假设x(n) 和h_{n-1} 统计独立，则：

E[x(n) x(n)^T h_{n-1}] = E[x(n) x(n)^T] E[h_{n-1}] = R_{xx} E[h_{n-1}]

令r_{dx} = E[x(n) d(n)]，则可写成：

E[h_n] = E[h_{n-1}] + \mu \bigl( r_{dx} - R_{xx} E[h_{n-1}] \bigr)

整理后：

E[h_n] = (I - \mu R_{xx}) E[h_{n-1}] + \mu r_{dx} \tag{1}

2. 误差向量定义

Wiener 解h_{\text{opt}} 满足：

R_{xx} h_{\text{opt}} = r_{dx}

即：

h_{\text{opt}} = R_{xx}^{-1} r_{dx}

定义误差向量：

\delta h_n = E[h_n] - h_{\text{opt}}

  • \delta h_n 表示当前估计的系数向量的期望值与最优解的偏差。

3. 误差向量的迭代公式

由 (1) 式：

E[h_n] = (I - \mu R_{xx}) E[h_{n-1}] + \mu r_{dx}

带入E[h_n] ：

\delta h_n + h_{\text{opt}} = (I - \mu R_{xx}) (\delta h_{n-1} + h_{\text{opt}}) + \mu r_{dx}

展开右边：

\delta h_n + h_{\text{opt}} = (I - \mu R_{xx}) \delta h_{n-1} + (I - \mu R_{xx}) h_{\text{opt}} + \mu r_{dx}

由于r_{dx} = R_{xx} h_{\text{opt}}，则：

\mu r_{dx} = \mu R_{xx} h_{\text{opt}}

因此：

(I - \mu R_{xx}) h_{\text{opt}} + \mu R_{xx} h_{\text{opt}} = h_{\text{opt}}

最终得到：

\delta h_n = (I - \mu R_{xx}) \delta h_{n-1} \tag{2}

4. 收敛条件

误差向量\delta h_n 经过(I - \mu R_{xx}) 的迭代，如果(I - \mu R_{xx}) 的特征值模小于1，则误差逐步缩小，则\delta h_n 逐步趋于0。考虑R_{xx} 的特征值分解， R_{xx} 的特征值为\lambda_i > 0， (I - \mu R_{xx}) 的特征值为1 - \mu \lambda_i。

要求：

|1 - \mu \lambda_i| < 1, \quad \forall i

即：

-1 < 1 - \mu \lambda_i < 1

整理得：

0 < \mu \lambda_i < 2

由于\lambda_{\max} 为最大特征值，最严格的条件是：

0 < \mu < \frac{2}{\lambda_{\max}}

证毕 

理论最大值为： 

\mu = \frac{2}{\lambda_{\text{max}}} = \frac{2}{8.6236} = 0.2319

 其中\lambda_{\text{max}} 由 Matlab 确定。详细解释后续补充 

% 计算 R_xx 的特征值
lambda = eig(R_xx);

% 找到最大特征值
lambda_max = max(lambda);

% 根据公式计算理论上使算法收敛的最大步长 mu_theorique_max
mu_theorique_max = 2 / lambda_max;

% 显示结果
disp('理论最大步长 mu_theorique_max:');
disp(mu_theorique_max);

由于理论计算是在以下假设条件下完成的：输入信号是平稳的，信道模型是精确的。而在实践中，真实信号并不总是满足这些假设。因此，应适当降低\mu 的值。在我们的案例中，选择\mu = 0.01。

 

我们现在改变滤波器的阶数L 和噪声水平\sigma^2_u，以测试算法的鲁棒性。特别是，绘制误差范数|h_n - h_{\text{opt}}|_2 随\sigma^2_u 的变化曲线。

对于不同 L 值，误差范数在各 σ_u 值下的函数

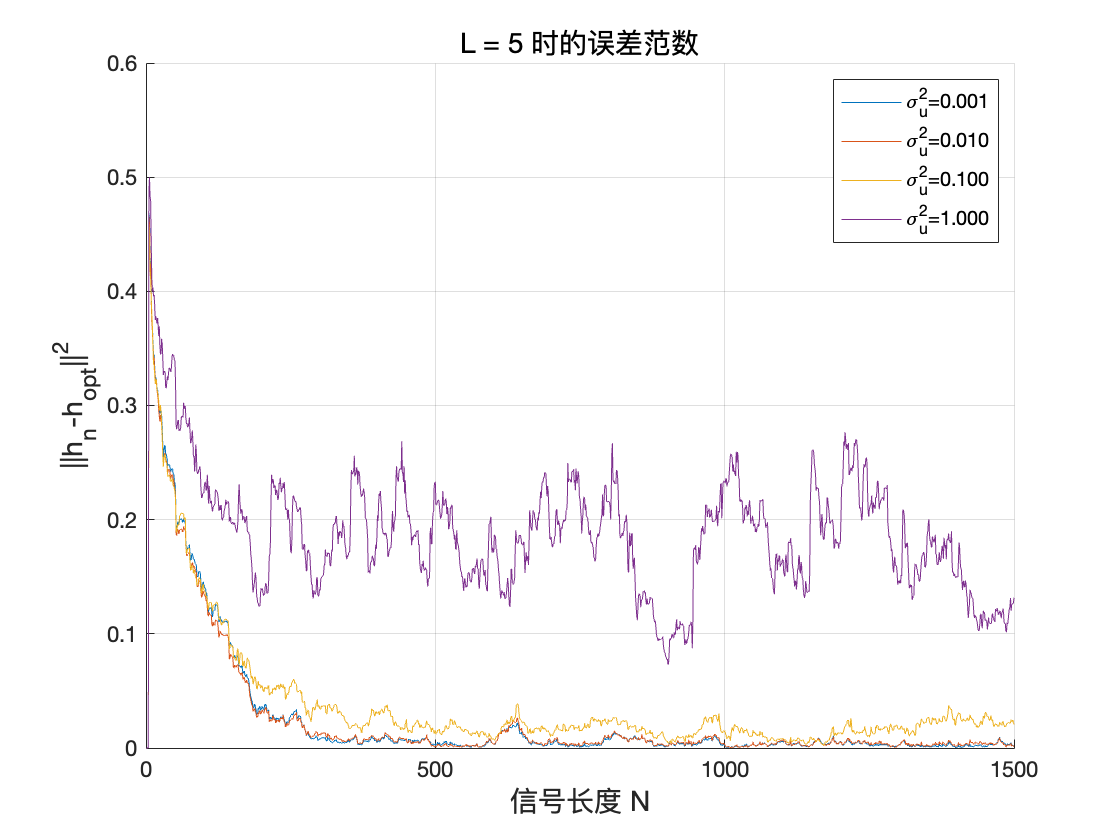
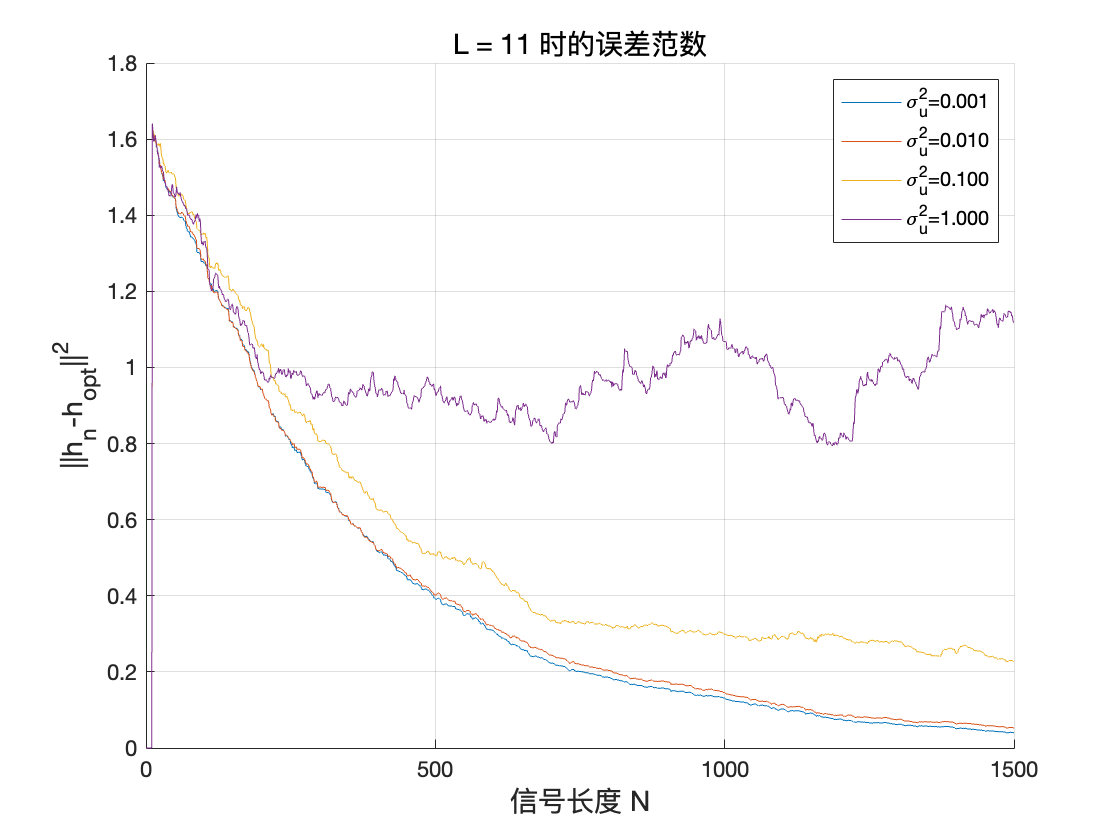
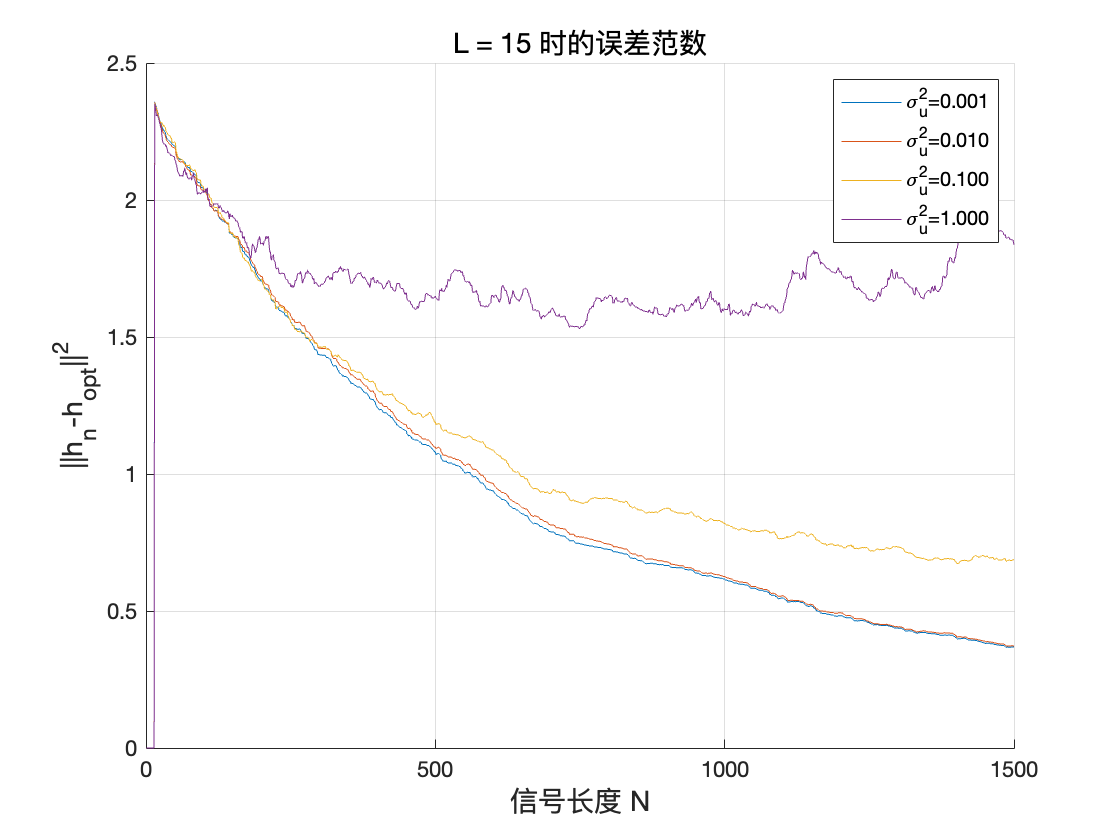
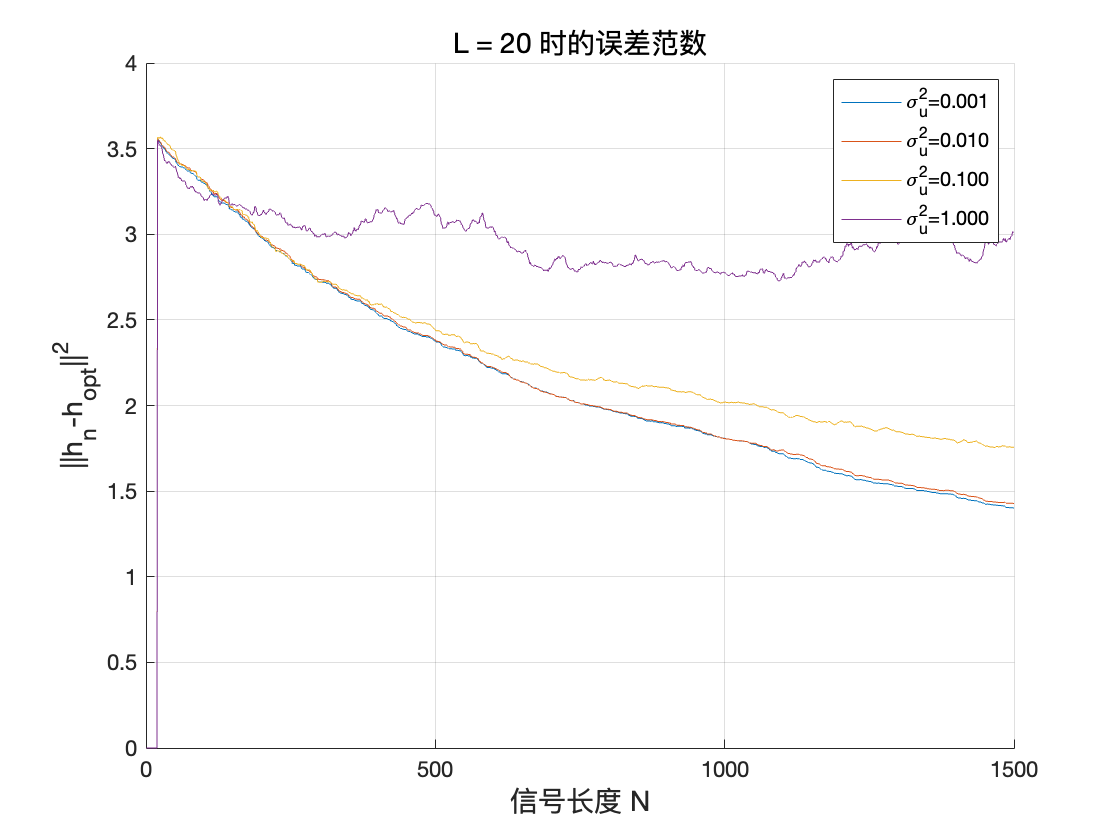
随着滤波器阶数的增加，振荡逐渐减弱，从快速收敛但振荡到收敛缓慢但稳定。

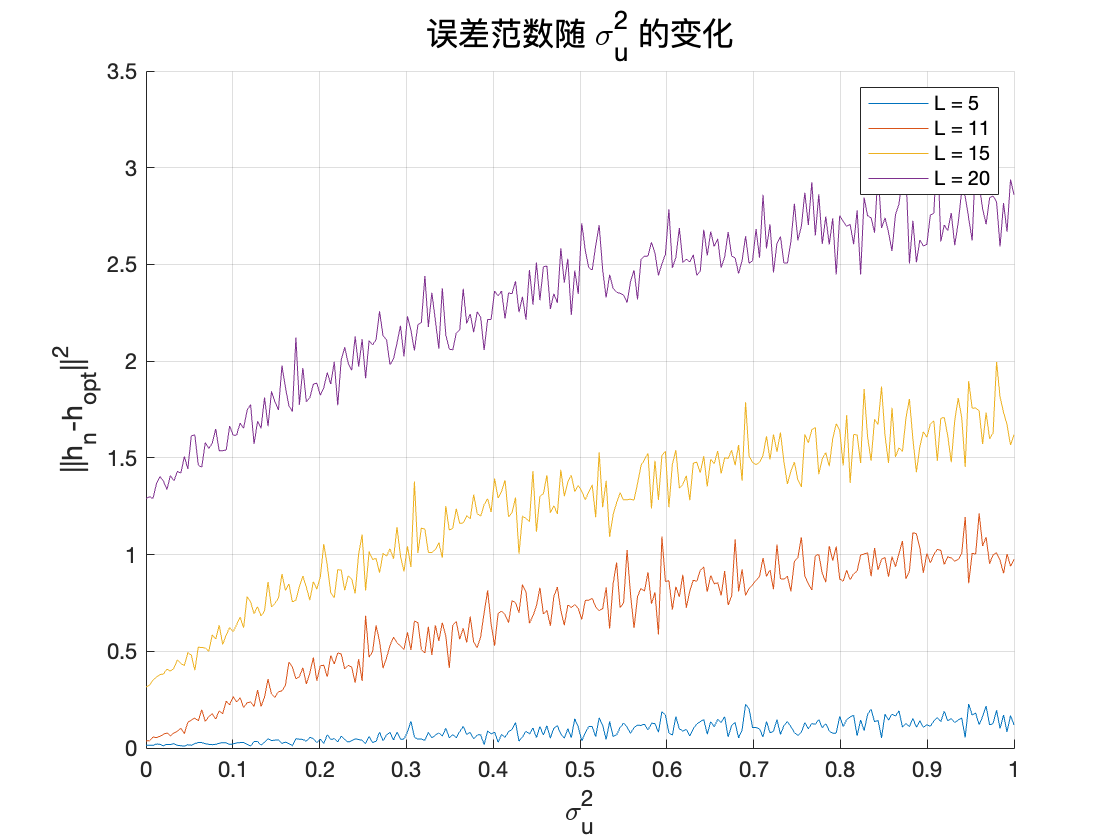
当输入信号（或噪声）方差 σ_u^2 不断增大时，用随机梯度算法估计到的滤波器 h_n 与最优滤波器 h_{opt} 之间的误差范数也随之增大。此外，在相同 σ_u^2 下，滤波器长度越大，最终估计误差也越明显。这说明在噪声方差较大时，估计更长的滤波器需要更多样本或更精细的调参，否则算法在均衡过程中会受到更强的随机扰动，导致估计结果与最优解的偏差增大。

#信号处理 14 #滤波器 2
3D重建理论
无约束优化