问题描述

我们将先研究Rosenbrock函数的最小化问题，它是非凸优化问题的经典测试函数，具有一个狭长的谷地（valley），其数学定义如下：

涉及的具体内容如下

(a) 创建和可视化Rosenbrock函数的二维和三维图像。

(b) 分析函数的性质，特别是其Convex性和优化难度。

(c) 计算并实现函数的梯度和Hessian矩阵。

(d) 利用梯度下降法以寻找函数的最小值。

%% 定义Rosenbrock函数及其网格数据
f = @(x1, x2) (1 - x1).^2 + 100*(x2 - x1.^2).^2;
​
% 定义绘图范围
x1 = linspace(-2,2,150);
x2 = linspace(-0.5,3,150);
[X1,X2] = meshgrid(x1,x2);
F = f(X1,X2);
​
% 全局最优点
x_star = [1; 1];
​
%% 可视化：3D表面图
figure;
surf(x1,x2,F);
xlabel('X_1'); ylabel('X_2'); zlabel('f(x_1,x_2)');
shading interp; camlight; axis tight;
title('Rosenbrock函数的3D表面图');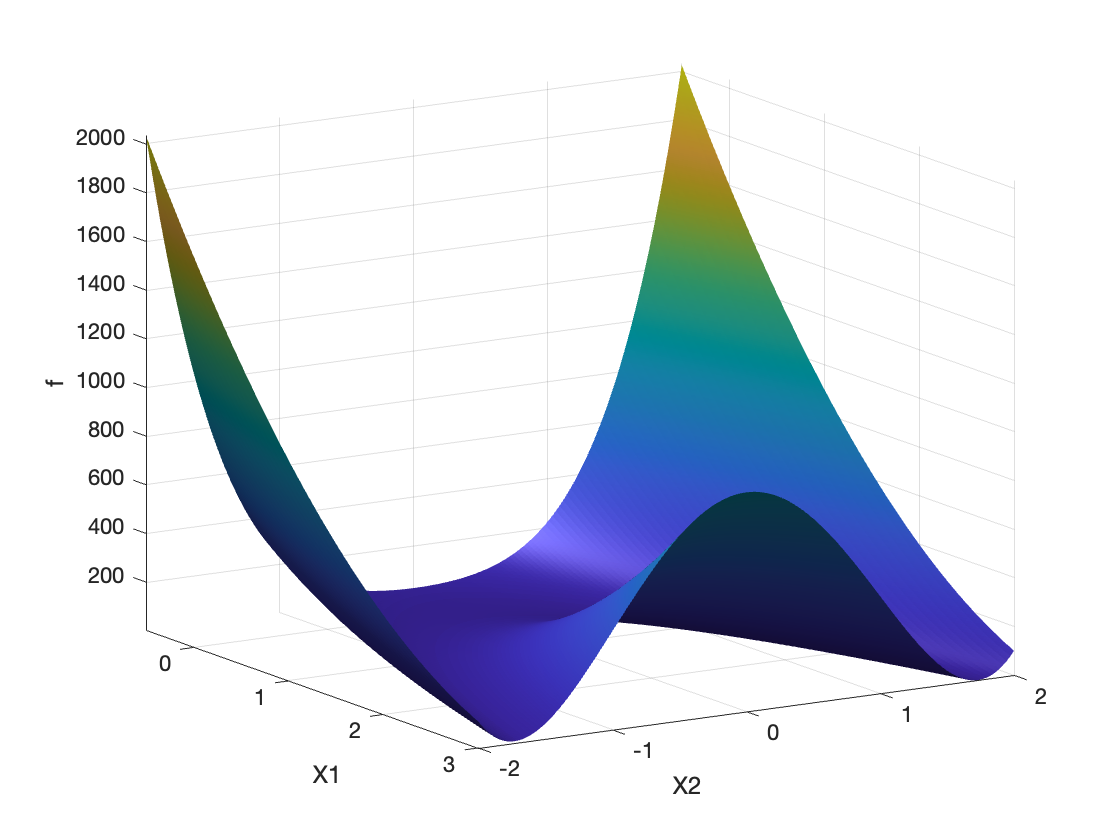

图1：Rosenbrock函数Convex性的3D显示

​可以注意到，Rosenbrock函数并非严格Convex的，有点类似局部Convex的感觉，其形状类似倒置的抛物线。随便在这个范围内两个点之间画一条直线，该直线会超出集合的界限。

因此，优化Rosenbrock函数具有一定难度。下降法可能会很容易陷入局部极小值，或在其周围振荡而无法收敛到全局极小值。

%% 2D热度图与等高线图
% 在深入分析前，先通过热度图和等高线图对函数有更直观的认识。
​
% 绘制热度图（保持x2为横轴、x1为纵轴，以符合meshgrid约定）
figure;
imagesc(x2, x1, F); axis xy;            
colormap jet(256); 
colorbar;
xlabel('X_2'); ylabel('X_1');
title('Rosenbrock函数的2D热度图（x_2为横轴，x_1为纵轴）');
hold on;
% 在热度图上标注全局最优点
plot(x_star(2), x_star(1), 'r*', 'MarkerSize', 8, 'LineWidth',2);
text(x_star(2)+0.1, x_star(1)+0.1, '最优点(1,1)','Color','r','FontSize',10);
hold off;
​
% 绘制等高线图（以x_1为横轴，x_2为纵轴），并在图中标记最优点
figure; 
contour_levels = 10;
contour(x1,x2,F,contour_levels);
xlabel('X_1'); ylabel('X_2');
title('Rosenbrock函数等高线图（标记全局最优点）');
hold on; 
plot(x_star(1), x_star(2), '*r', 'MarkerSize',10, 'LineWidth',2);
plot([x_star(1) x_star(1)], [min(x2) max(x2)], 'r--', 'LineWidth',1.2);
plot([min(x1) max(x1)], [x_star(2) x_star(2)], 'r--', 'LineWidth',1.2);
text(x_star(1)+0.1, x_star(2)+0.1, '最优点(1,1)', 'Color','r','FontSize',10);
hold off;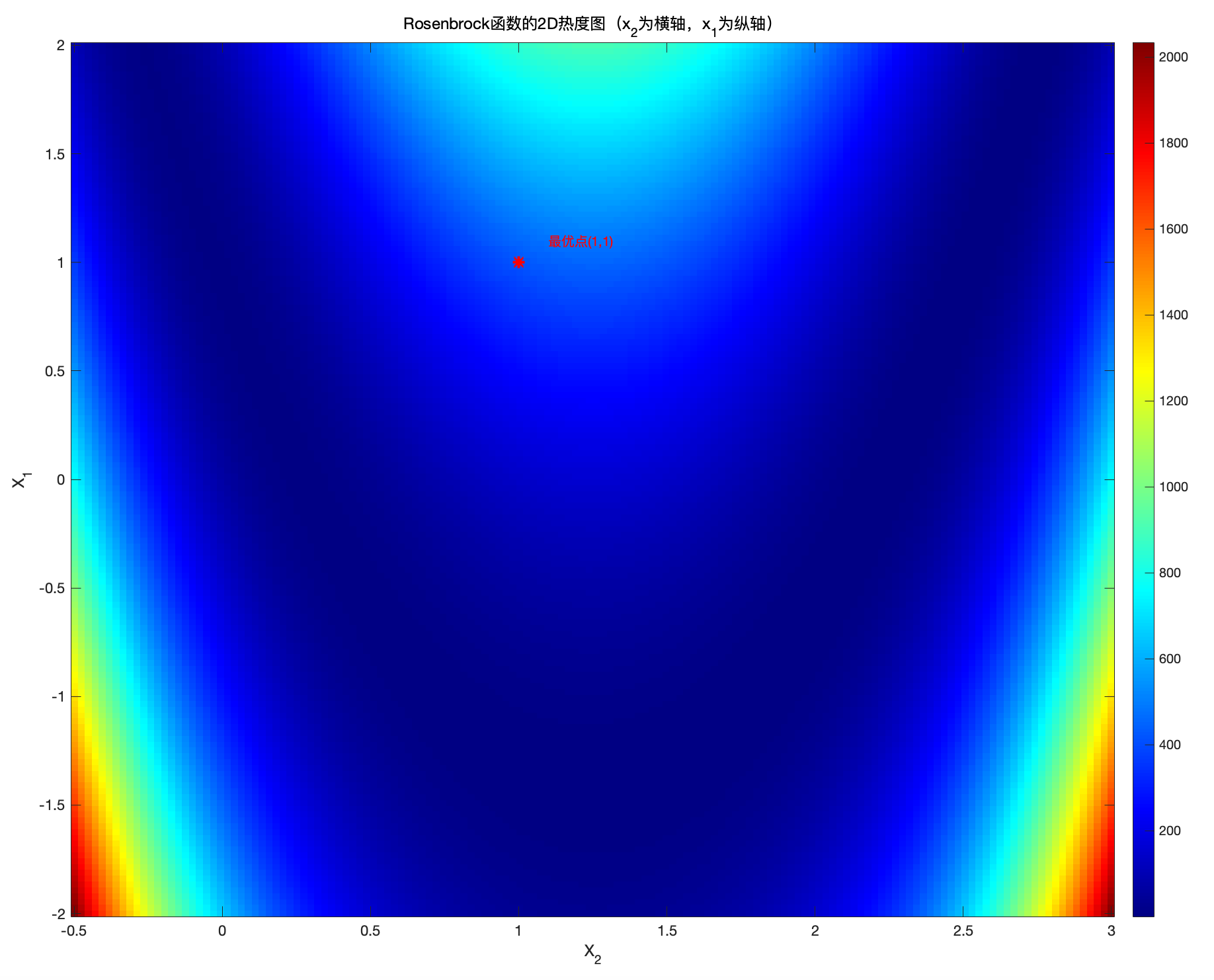

​

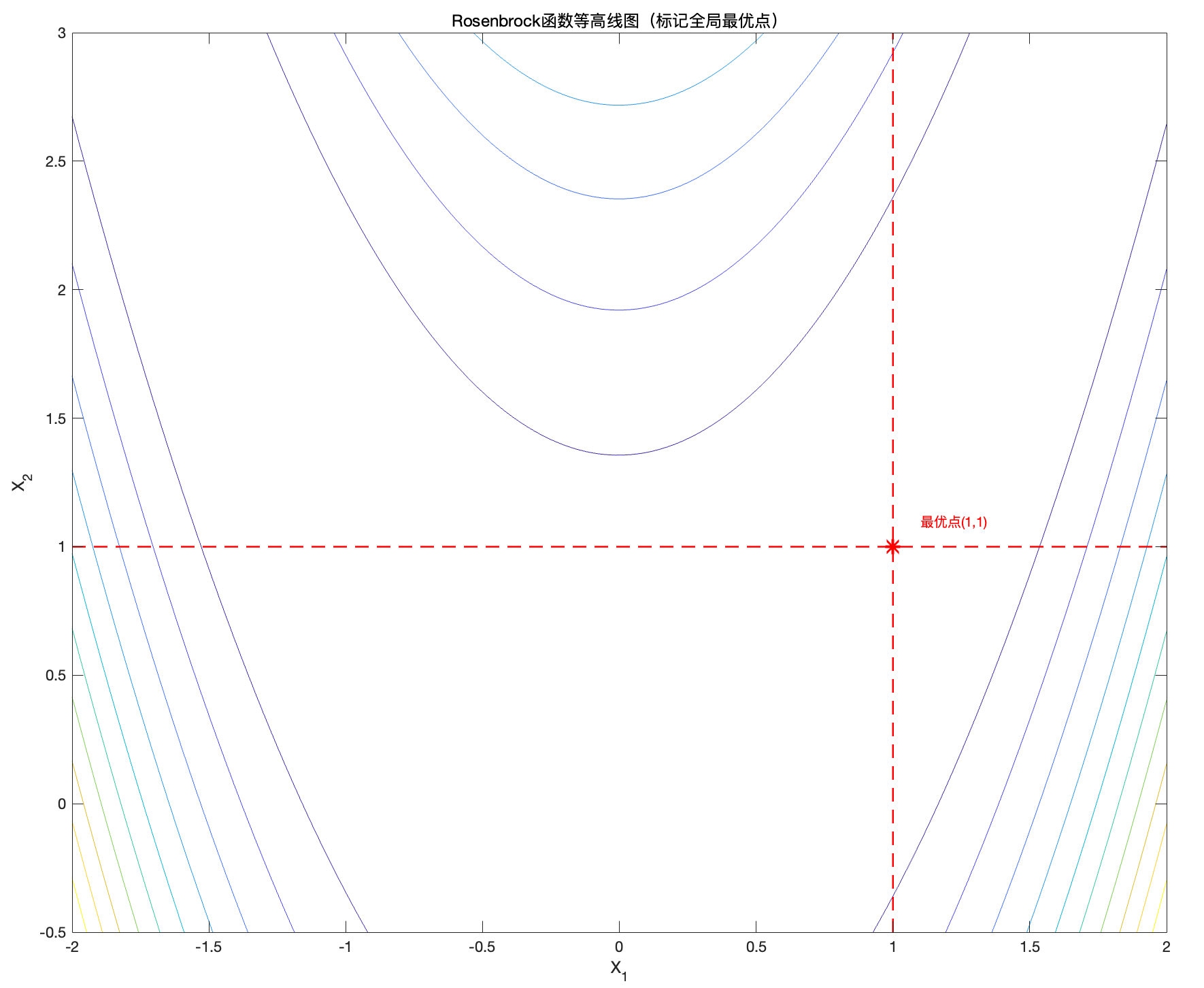
图2：Rosenbrock函数的2D热度图和等高线图

等高线表示相同函数值的点的集合，梯度始终垂直于等高线，因此

• 等高线密集 → 梯度较大（函数值变化快，斜率陡峭）

• 等高线稀疏 → 梯度较小（函数值变化慢，斜率平缓）

于此同时，我们还可以看出优化算法在 Rosenbrock 函数上收敛较慢，因为函数的梯度变化不均匀。

前置计算

我们下面计算函数f 的梯度

梯度的表达方式如下：

计算 \frac{\partial f}{\partial x_1} ：

计算 \frac{\partial f}{\partial x_2} ：

因此，函数f 的梯度为：

可以进一步计算Hessian矩阵：

因此需要解以下系统方程：

可得到:

​我们把上述公式带回第一个方程后，发现不好求，因此我们使用眼瞅法，打眼一看，在 x^* = (1, 1) 应该行， 我们带入验证后发现梯度确实为0

因此我们验证了​平衡点：

在平衡点 x^* = (1, 1) 处计算Hessian矩阵：

我们利用Matlab求解Hessian矩阵的特征值，如果特征值为正，那么可以说明点 x^{*} = (1, 1)是一个最小值

%% Hessian矩阵特征值分析（验证局部最小性的充分条件）
Hj = [802 -400; -400 200];
disp('Hj的特征值:');
disp(eig(Hj));
% 特征值均为正数，说明此处Hj对应点为局部最小点（正定矩阵）

因此，两个特征值均为严格正值，表明Hessian矩阵是正定的，点 x^* = (1, 1)是一个局部最小值。

编程实现梯度 和 Hessian矩阵

%% 定义梯度与Hessian函数
gradf = @(x1, x2) [-2 + 2*x1 - 400*x1*x2 + 400*x1^3; 200*x2 - 200*x1^2];
Gradf = @(x) gradf(x(1), x(2));
​
hessf = @(x1, x2) [2 - 400*x2 + 1200*x1^2, -400*x1; -400*x1, 200];
Hessf = @(x) hessf(x(1), x(2));

后续我们将比较两种优化方法：一种是经典梯度下降法，另一种是牛顿法。

梯度下降法

梯度下降法是一种迭代优化技术，用于寻找可微函数的最小值。其基本思想是沿着目标函数梯度的反方向移动，因为这一方向可以使函数值下降最快。其过程如下：

(a) 选择初始点 x_0 ，该点位于函数定义域内。

(b) 在每次迭代 k 中，计算函数的梯度 \nabla f(x_k) 。

(c) 根据以下规则更新当前点：

其中， \alpha 是下降步长（学习率），为控制步长大小的正参数。

(d) 迭代过程重复，直到梯度足够接近于零（或者达到最大迭代次数）。

(e) 在每次迭代中使用相同的 \alpha 。选择合适的 \alpha 至关重要：步长太大会导致算法震荡甚至发散，而步长太小会减慢收敛速度。

梯度下降法的优点在于其简单易用，并且可以适用于广泛的可微函数和优化问题。然而，它也存在以下缺点：

• 收敛速度可能较慢，特别是对于类似于 Rosenbrock函数 的问题。

• 不适当的步长选择可能会阻止收敛。

• 对于非Convex函数，梯度下降可能陷入局部最小值。

接下来我们将通过编程，在Rosenbrock函数上实现梯度下降法，以确定函数 f 的最小值。

%% 使用梯度下降法（Gradient Descent）示例
% 演示从某初始点开始的迭代路径，显示在等高线图上
figure; hold on;
contour(x2, x1, F,10);
xlabel('X_2'); ylabel('X_1');
title('梯度下降法优化路径示意图');
alpha = 1e-4;          % 步长
x0 = [1.5;2.5];        % 初始点
N = 1e5;               % 迭代次数上限
[x_path, fx_path] = descente_gradient(f, Gradf, N, alpha, x0);
​
% 绘制迭代点的移动轨迹
plot(x_path(2,:), x_path(1,:), 'k', 'linewidth', 1.5);
plot(x_path(2,end), x_path(1,end), 'ro', 'MarkerSize',6, 'LineWidth',2);
text(x_path(2,end)+0.05, x_path(1,end), '收敛点','Color','r','FontSize',8);
axis([-.5 3 -2 2]);
hold off;

function [x, fx] = descente_gradient(f, Gradf, N, alpha, x0)
    x = zeros(length(x0), N+1);
    fx = zeros(1, N+1);
    x(:,1) = x0;
    fx(1) = f(x0(1),x0(2));
    for i = 1:N
        x(:,i+1) = x(:,i) - alpha*Gradf(x(:,i));
        fx(i+1) = f(x(1,i+1), x(2,i+1));
    end
end

得到以下图像：

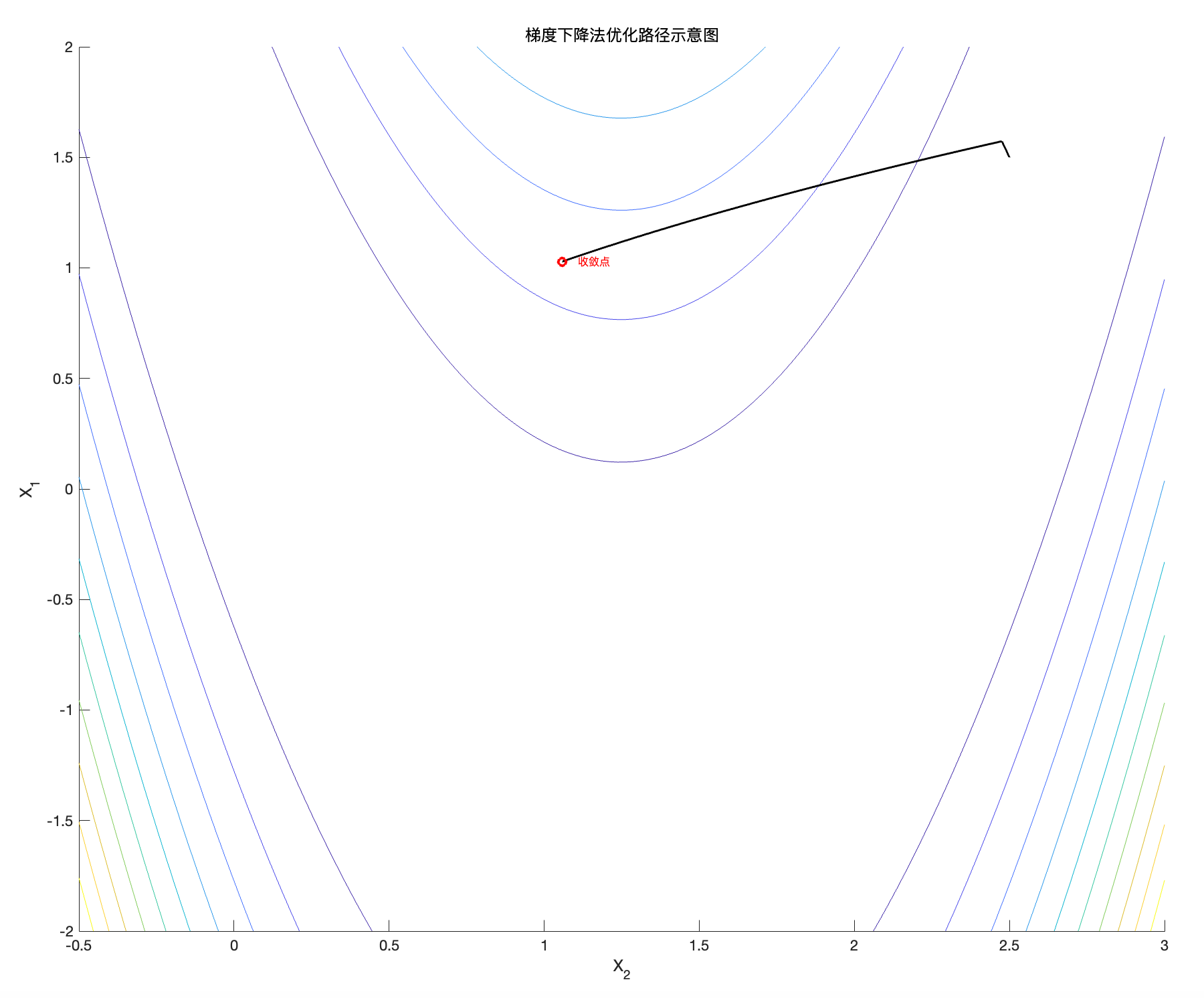
图3：Rosenbrock函数的梯度下降轨迹（ N = 10^5 ）

通过图3可以观察到，轨迹一开始有一个小波动，在初始几步中找不到最佳下降方向很正常，这是由于Rosenbrock函数的特性所致。然而，随着迭代进行，路径变得非常规则，算法逐步收敛至全局最小值

为了说明迭代次数和步长的重要性，我们尝试不同参数下的下降过程。

首先，将迭代次数从 100000 减少到 10000 。

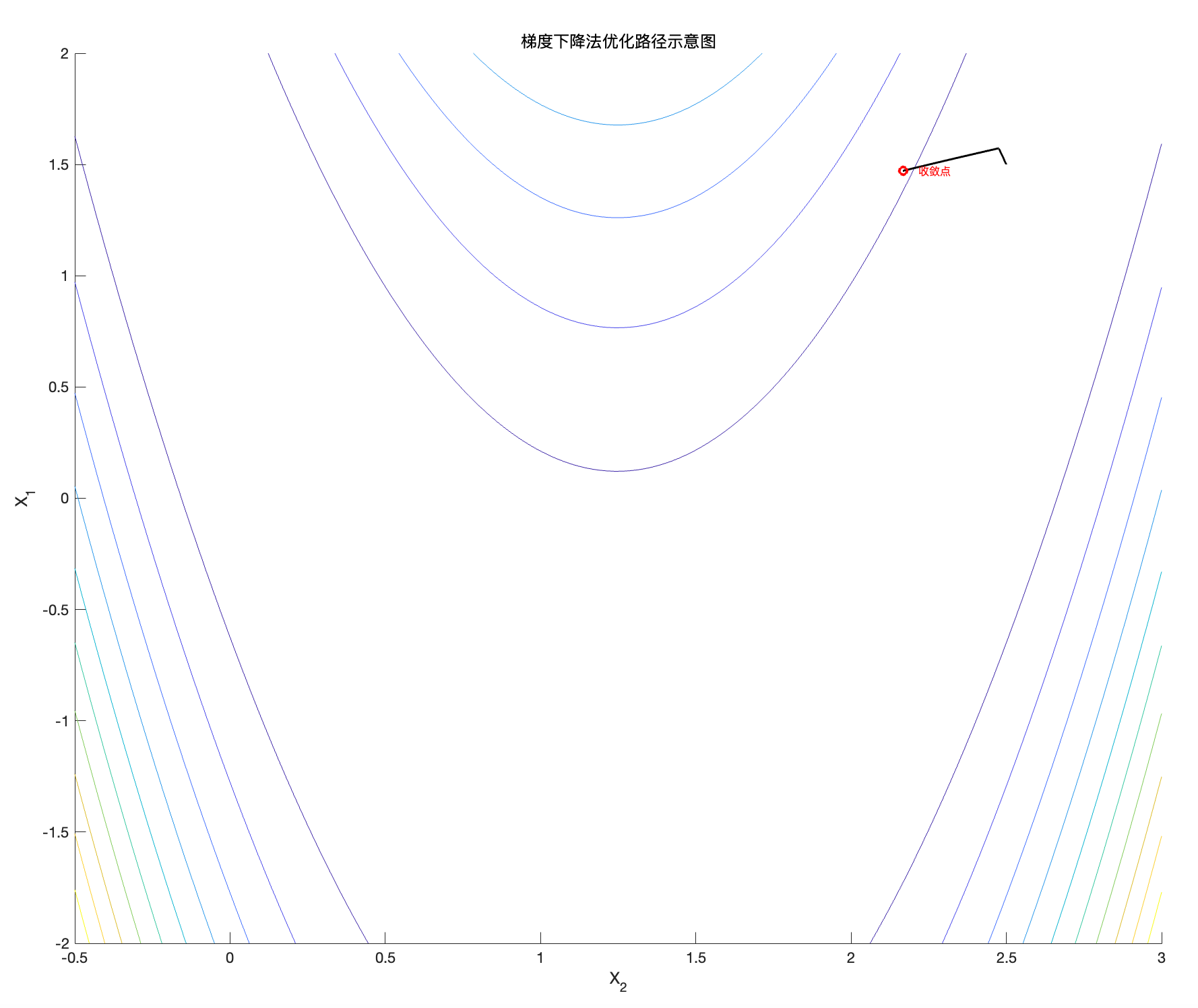
图4：Rosenbrock函数的梯度下降轨迹（ N = 10^4 ）

可见算法没走完，迭代次数不够。

现在对于梯度下降轨迹已经分析完了，下面调步长 \alpha ，看看它对算法性能的影响，并理解如何影响优化的稳定性、收敛速度以及精度。

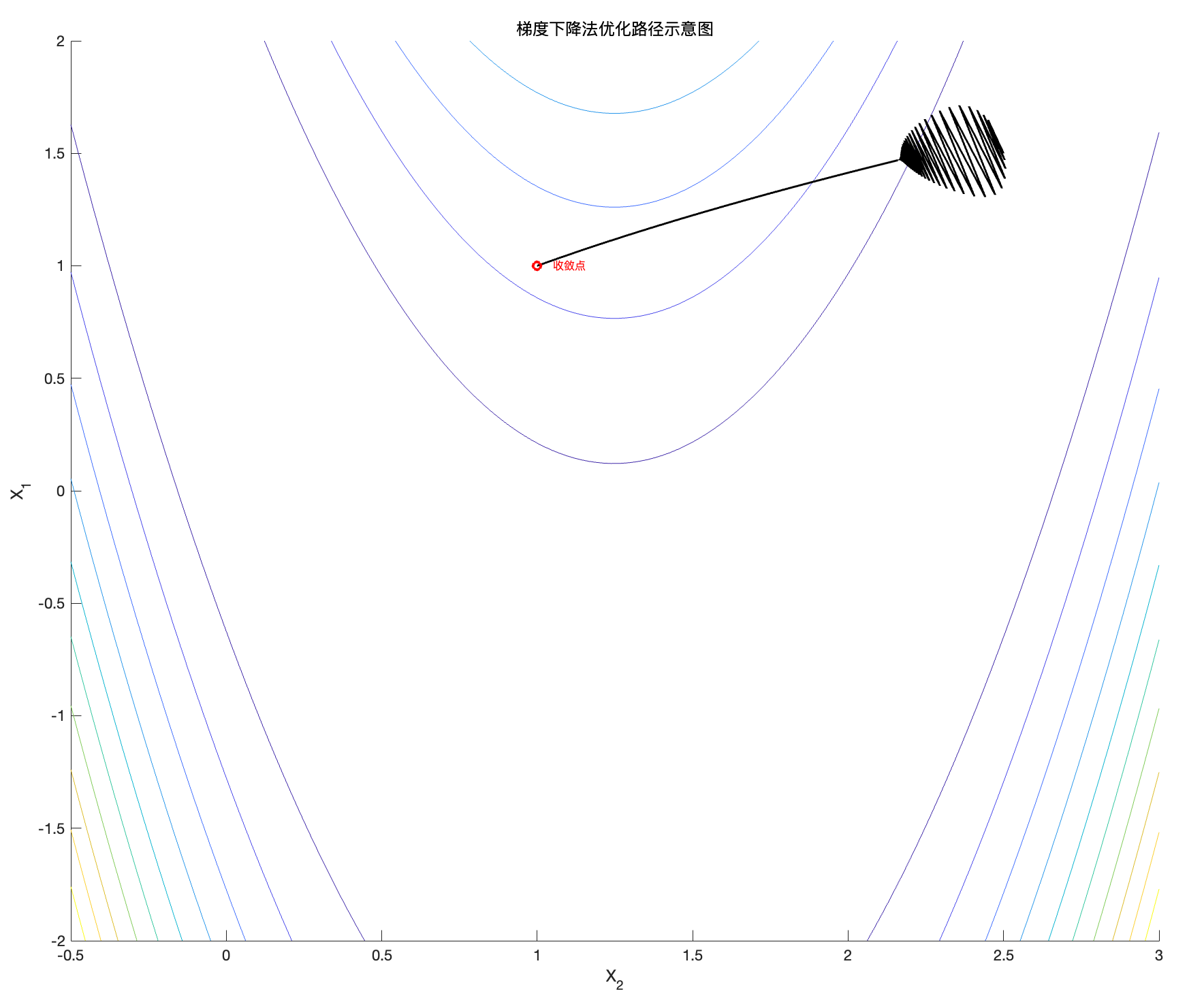
图5：Rosenbrock函数的梯度下降轨迹（ \alpha = 10^{-3}）

\alpha 增大了，可见算法有点激进，但是还救的回来。

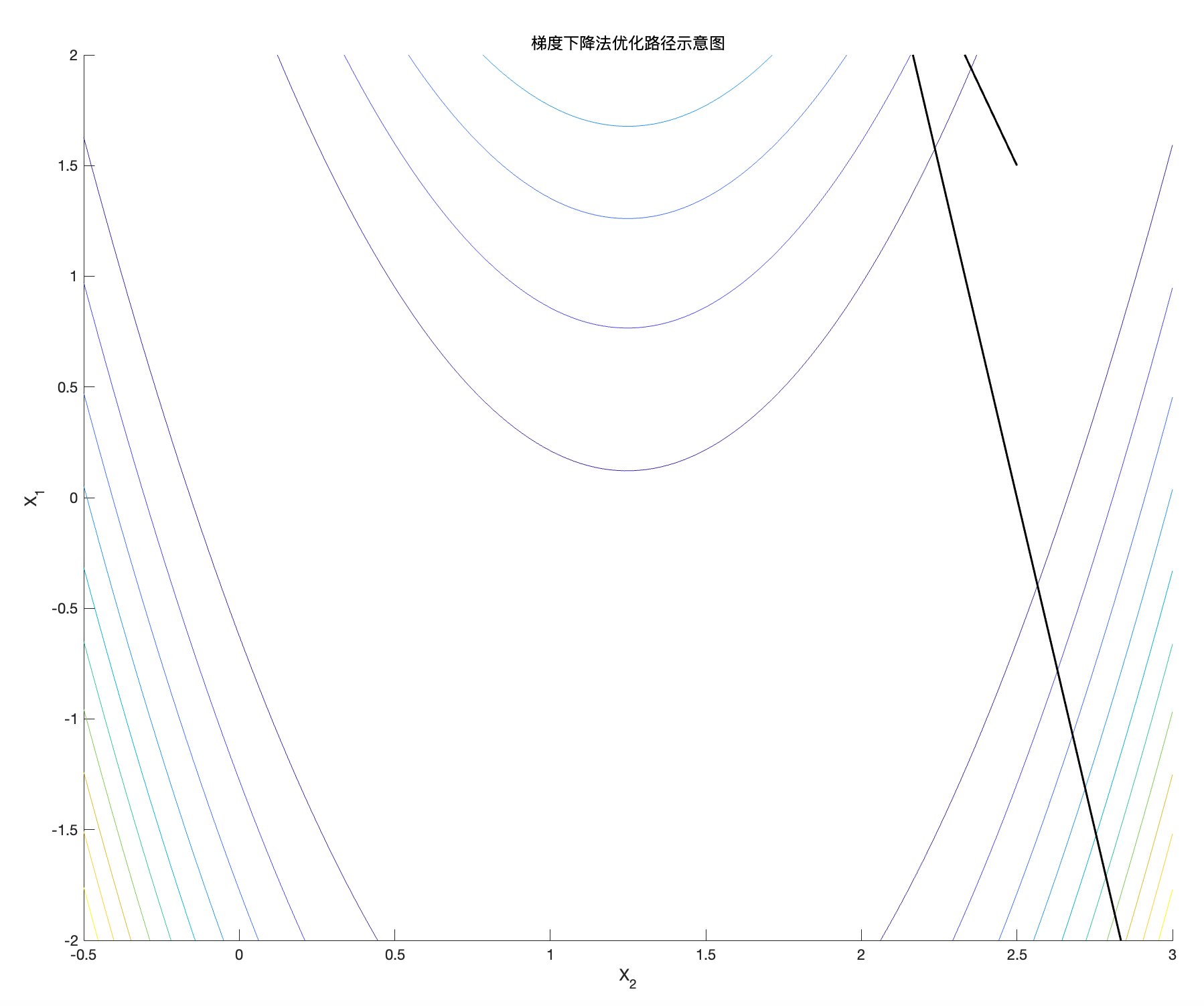
图6：Rosenbrock函数的梯度下降轨迹（ \alpha = 10^{-2} ）

轨迹不再收敛，开始震荡并发散。步长 \alpha = 10^{-2} 过大，远离最优解，一个跟头跑出十万八千里外了。

给出最优解

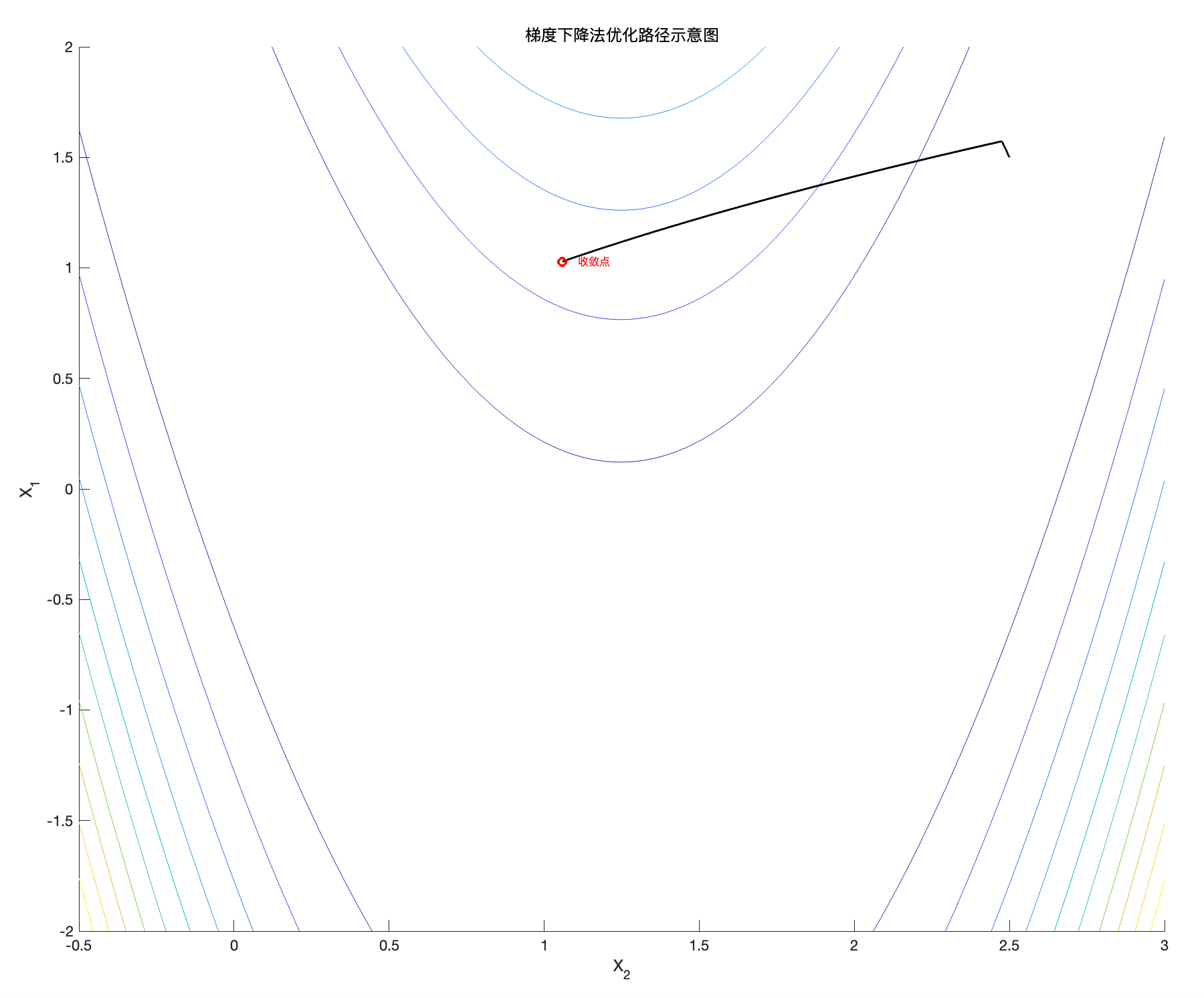
图7：Rosenbrock函数的梯度下降轨迹（ \alpha = 10^{-4}, N = 10^5 ）

非常漂亮，不需要解释了

我们需要在步长和迭代次数之间找到一个良好的平衡，以使算法在有限的迭代次数和适当的步长下收敛到最小值，同时避免过多的震荡，从而节省计算成本和时间。

改进方法:

每次迭代中，不仅考虑当前梯度，还要考虑先前迭代的方向，这可以减少震荡并加速收敛。或者结合其他优化方法，例如牛顿法，其利用了 Hessian矩阵来提高收敛速度和精度。​

牛顿法

牛顿法是一种迭代优化技术，用于寻找可导函数的驻点。与梯度下降法不同，牛顿法不仅利用梯度信息，还使用函数曲率信息（Hessian矩阵）来确定下降方向。

其过程如下：

1. 选择一个初始点 x_0 ，位于函数定义域内。

2. 在每次迭代 k 中，计算函数的梯度 \nabla f(x_k) 和Hessian矩阵 H_f(x_k) 。

3. 根据以下规则更新当前点：

其中， H_f(x_k)^{-1} 是函数在点 x_k 处的Hessian矩阵的逆矩阵。

4. 重复该过程，直到梯度足够接近于零或更新步长的范数小于预设阈值。

牛顿法通过利用梯度和曲率信息，让更新更高效、收敛更快。但是，计算成本高，需要计算 Hessian 逆矩阵，并且在函数条件差或非Convex时不是很好用。

继续对Rosenbrock函数动手，利用Matlab实现，首先选择 N = 10 和 x_0 = [1.7; 2.7] 。

%% 使用Newton法优化示例（并显示收敛性）
figure; hold on;
contour(x2, x1, F,10);
xlabel('X_2'); ylabel('X_1');
title('Newton法优化路径示意图');
x0 = [1.7;2.7];  % 初始点
N = 10;
[x_path_N, fx_path_N] = descente_Newton(f, Gradf, Hessf, N, x0);
plot(x_path_N(2,:), x_path_N(1,:), 'k', 'linewidth', 1.5);
plot(x_path_N(2,end), x_path_N(1,end), 'ro', 'MarkerSize',6, 'LineWidth',2);
text(x_path_N(2,end)+0.05, x_path_N(1,end), '收敛点','Color','r','FontSize',8);
axis([-.5 3 -2 2]);
hold off;

function [x, fx] = descente_Newton(f, Gradf, Hessf, N, x0)
    x = zeros(length(x0), N+1);
    fx = zeros(1, N+1);
    x(:,1) = x0;
    fx(1) = f(x0(1),x0(2));
    for i = 1:N
        x(:,i+1) = x(:,i) - inv(Hessf(x(:,i)))*Gradf(x(:,i));
        fx(i+1) = f(x(1,i+1), x(2,i+1));
    end
end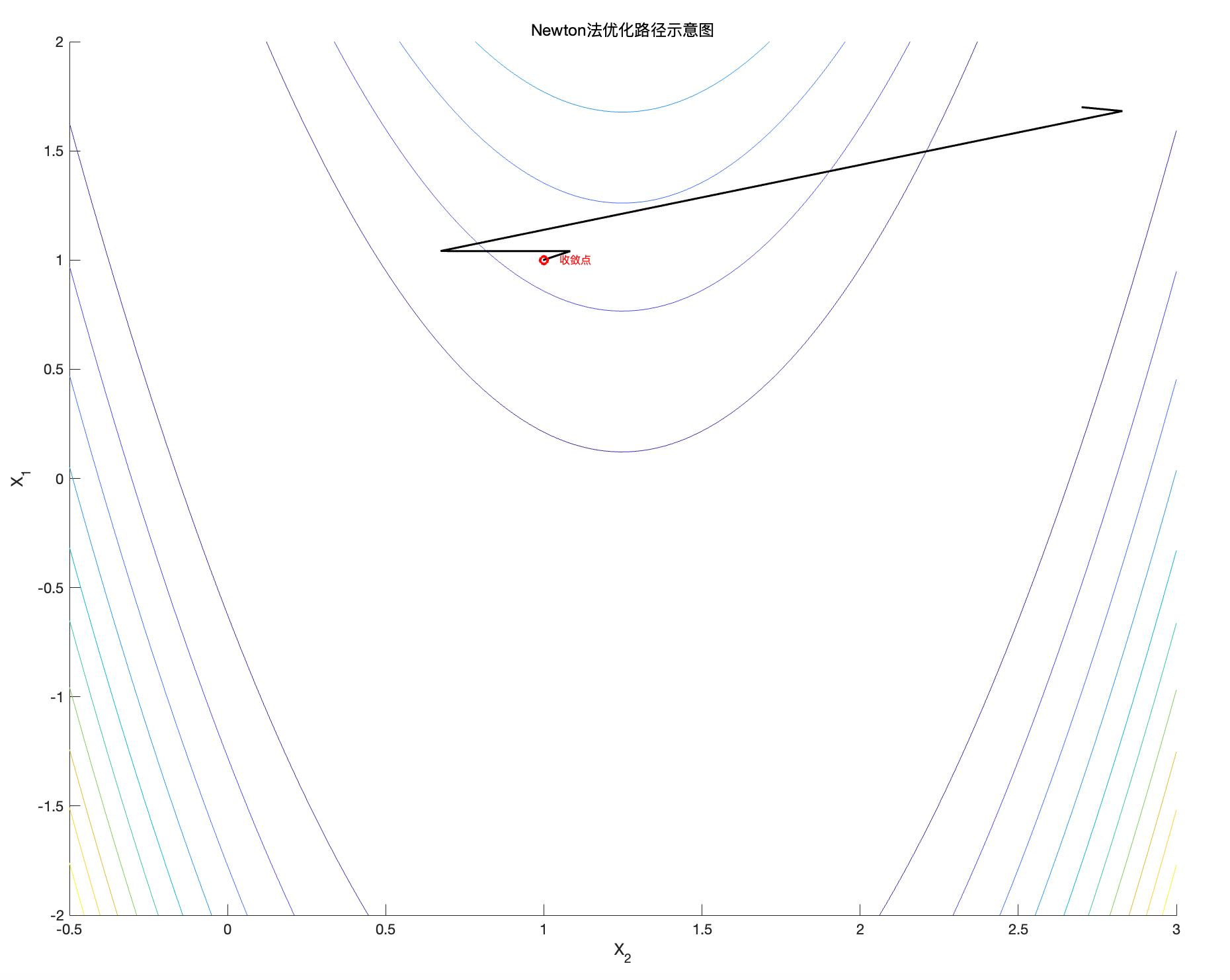

​

图8：Rosenbrock函数的牛顿法轨迹

​与梯度下降法类似，轨迹从右上角 向 最优点靠近。牛顿法收敛速度更快。

% 计算误差E
E = sqrt(sum((x_path_N - x_star).^2, 1));
​
% 绘制收敛性曲线（函数值与误差的对数对数图）
figure;
subplot(2,1,1);
plot(log10(1:N+1), log10(fx_path_N));
xlabel('Log10(Iteration)'); ylabel('Log10(f(x))');
title('Newton法对Rosenbrock函数收敛性（函数值）');
​
subplot(2,1,2);
plot(log10(1:N+1), log10(E));
xlabel('Log10(Iteration)'); ylabel('Log10(||x - x^*||)');
title('Newton法对Rosenbrock函数的误差收敛曲线');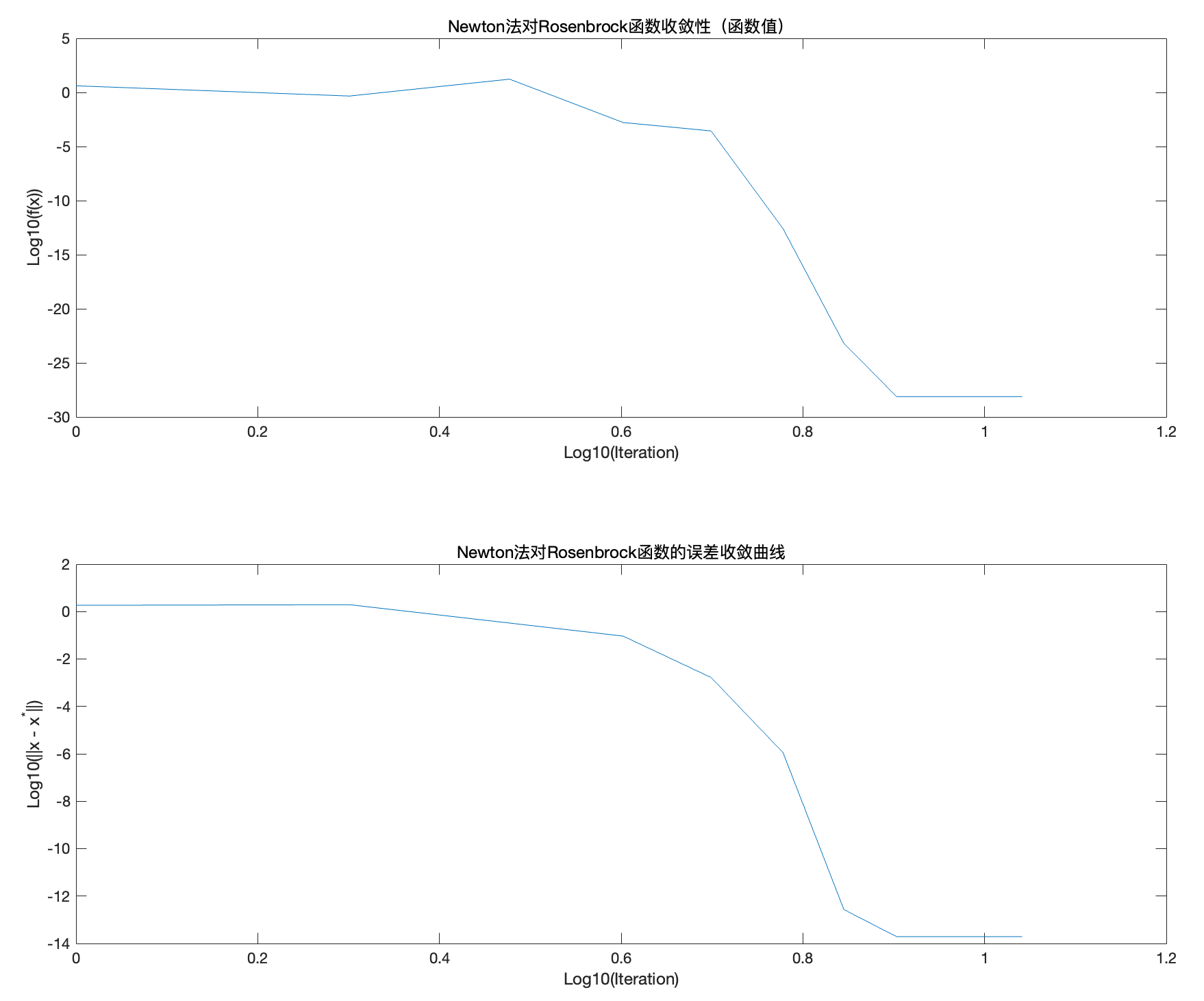

​

图9： f的变化与误差 e关于迭代次数的演变

我们绘制了两个图，用于描述函数f 和误差 e随迭代次数的变化。

对于Rosenbrock函数，纵轴表示函数值的对数刻度\log_{10}，横轴表示迭代次数的对数刻度\log_{10}。可以看到，在大约10^{0.6} 次迭代后，函数值迅速下降（约4次迭代）。然后曲线趋于稳定，接近10^{-30}，表明函数基本收敛到全局最小值。

对于牛顿算法，纵轴表示误差范数|x - x^*| 的对数刻度（ \log_{10}），横轴表示迭代次数的对数刻度（ \log_{10}）。可见误差范数随着迭代次数迅速下降，显示出算法的 快速收敛 性，因为通过利用Hessian矩阵加速了向最优解的下降。最后稳定在极低的值（ 10^{-15}），这表明x 与 x^* 之间的误差几乎为零，显示牛顿法精确地收敛到最优解。

可见牛顿法在优化Rosenbrock函数时非常不错，快速且精确。

%% 比较不同初始点对Newton法收敛路径的影响
figure; hold on;
contour(x2, x1, F,10);
plot(1, 1, '*k', 'MarkerSize', 14);
xlabel('X_2'); ylabel('X_1');
title('不同初始点下Newton法迭代路径对比');
​
cols = {'r', 'g', 'b'};
Xinit = {[-1.5;2.5], [1.7;2.7], [-0.3;0.85]};
N = 10;
​
for k = 1:length(Xinit)
    x0 = Xinit{k};
    [X_multi, f_X_multi] = descente_Newton(f, Gradf, Hessf, N, x0);
    plot(X_multi(2,:), X_multi(1,:), [cols{k} '*-'], 'MarkerSize', 8, 'linewidth', 1.5);
    text(X_multi(2,end)+0.05, X_multi(1,end), ['初始点收敛轨迹(' num2str(k) ')'], ...
        'Color',cols{k},'FontSize',8);
end
axis([-.5 3 -2 2]);
hold off;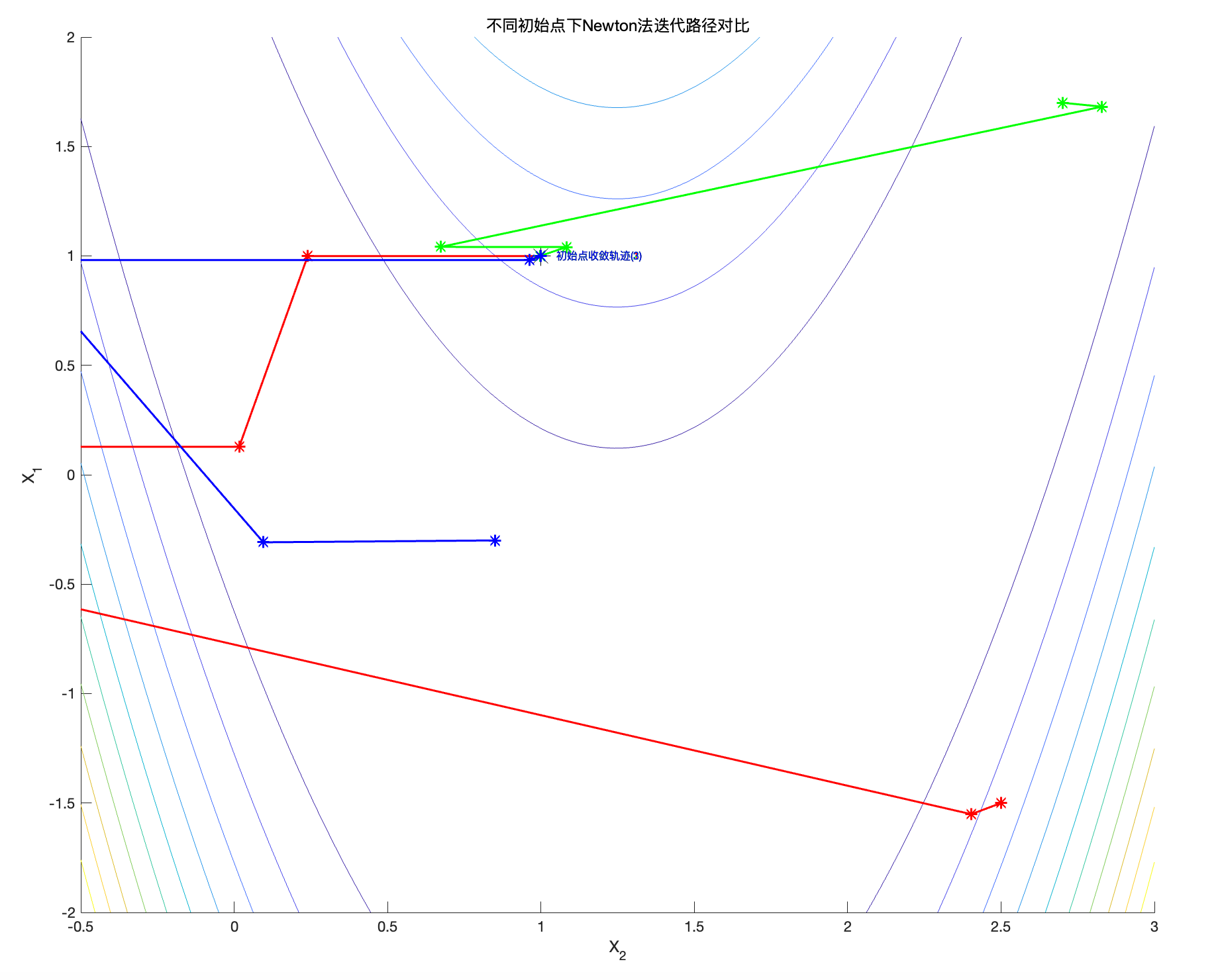

​

图10：不同初始化条件下解x 的演变

​我们从三个不同初始点（分别用红色、蓝色和绿色表示）来出发并显示它的轨迹。它们最终收敛到不同的点，但是距离非常接近，特别是绿色和蓝色。这表明牛顿法到达局部最小值或非常接近全局最小值的能力。即使初始条件不同，但是我们可能获得同样的最优解结果，这让初始点的策略选择变得不那么紧张了。

%% 在同一张等高线图中对比梯度下降法与牛顿法的迭代路径
figure; hold on;
contour(x2, x1, F,10);                 % 等高线
plot(x_star(2), x_star(1), '*k', 'MarkerSize',14); % 全局最优点标记
​
% 梯度下降法轨迹（已计算的x_path, fx_path）
plot(x_path(2,:), x_path(1,:), 'b.-', 'MarkerSize',10, 'LineWidth',1.5);
​
% 牛顿法轨迹（已计算的x_path_N, fx_path_N）
plot(x_path_N(2,:), x_path_N(1,:), 'ro-', 'MarkerSize',6, 'LineWidth',1.5);
​
xlabel('X_2'); ylabel('X_1');
title('梯度下降法 vs 牛顿法 优化路径对比');
legend('等高线','最优点','梯度下降法轨迹','牛顿法轨迹','Location','best');
hold off;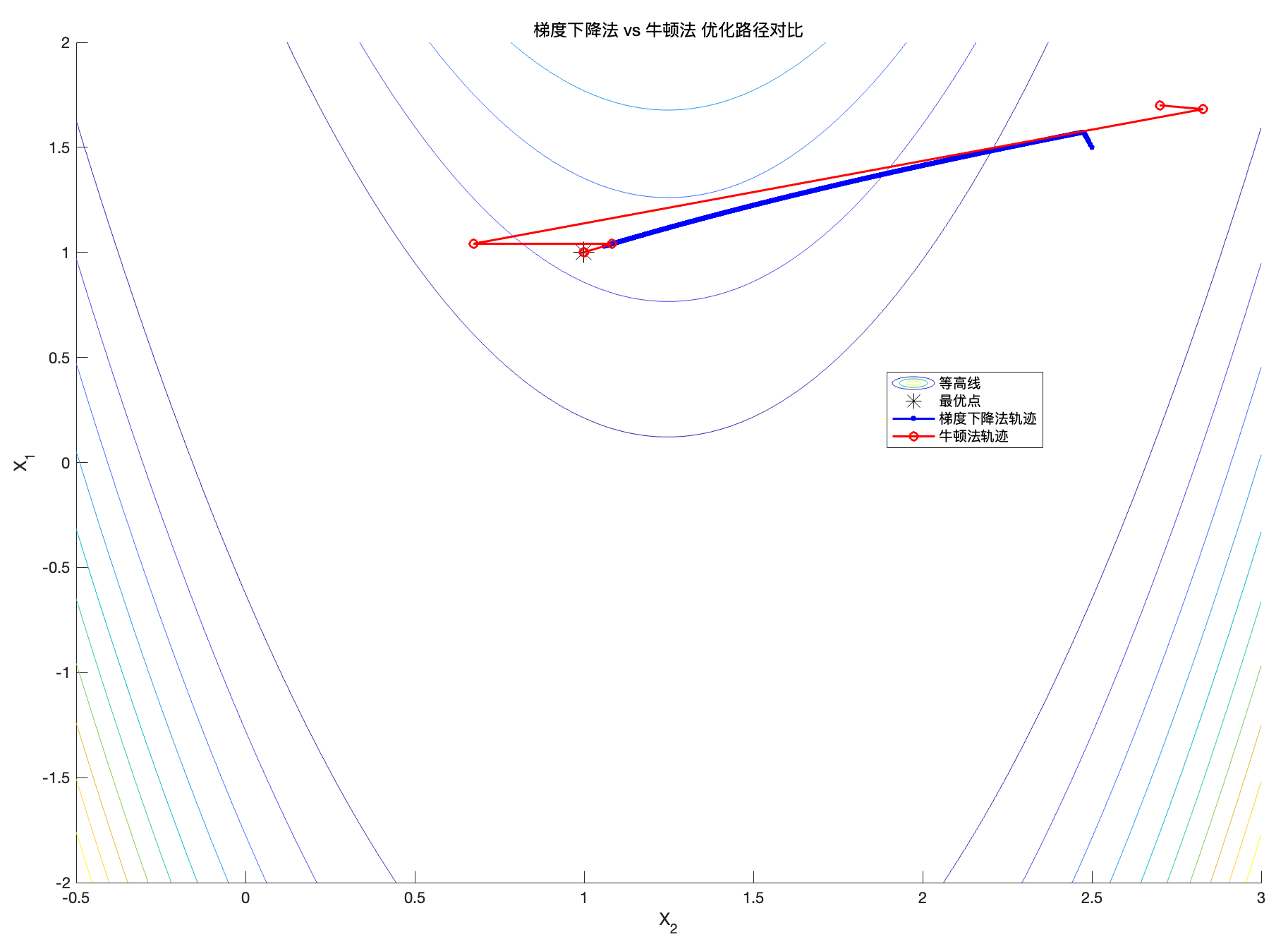

%% 对比函数值和误差的收敛过程（以对数尺度展示）
figure;
​
subplot(2,2,1);
plot(log10(1:length(fx_path)), log10(fx_path), 'b');
xlabel('Log10(Iteration)'); ylabel('Log10(f(x))');
title('梯度下降法函数值收敛(对数尺度)');
​
subplot(2,2,2);
plot(log10(1:length(E_gd)), log10(E_gd), 'b');
xlabel('Log10(Iteration)'); ylabel('Log10(||x - x^*||)');
title('梯度下降法误差收敛(对数尺度)');
​
subplot(2,2,3);
plot(log10(1:length(fx_path_N)), log10(fx_path_N), 'r');
xlabel('Log10(Iteration)'); ylabel('Log10(f(x))');
title('牛顿法函数值收敛(对数尺度)');
​
subplot(2,2,4);
plot(log10(1:length(E_newton)), log10(E_newton), 'r');
xlabel('Log10(Iteration)'); ylabel('Log10(||x - x^*||)');
title('牛顿法误差收敛(对数尺度)');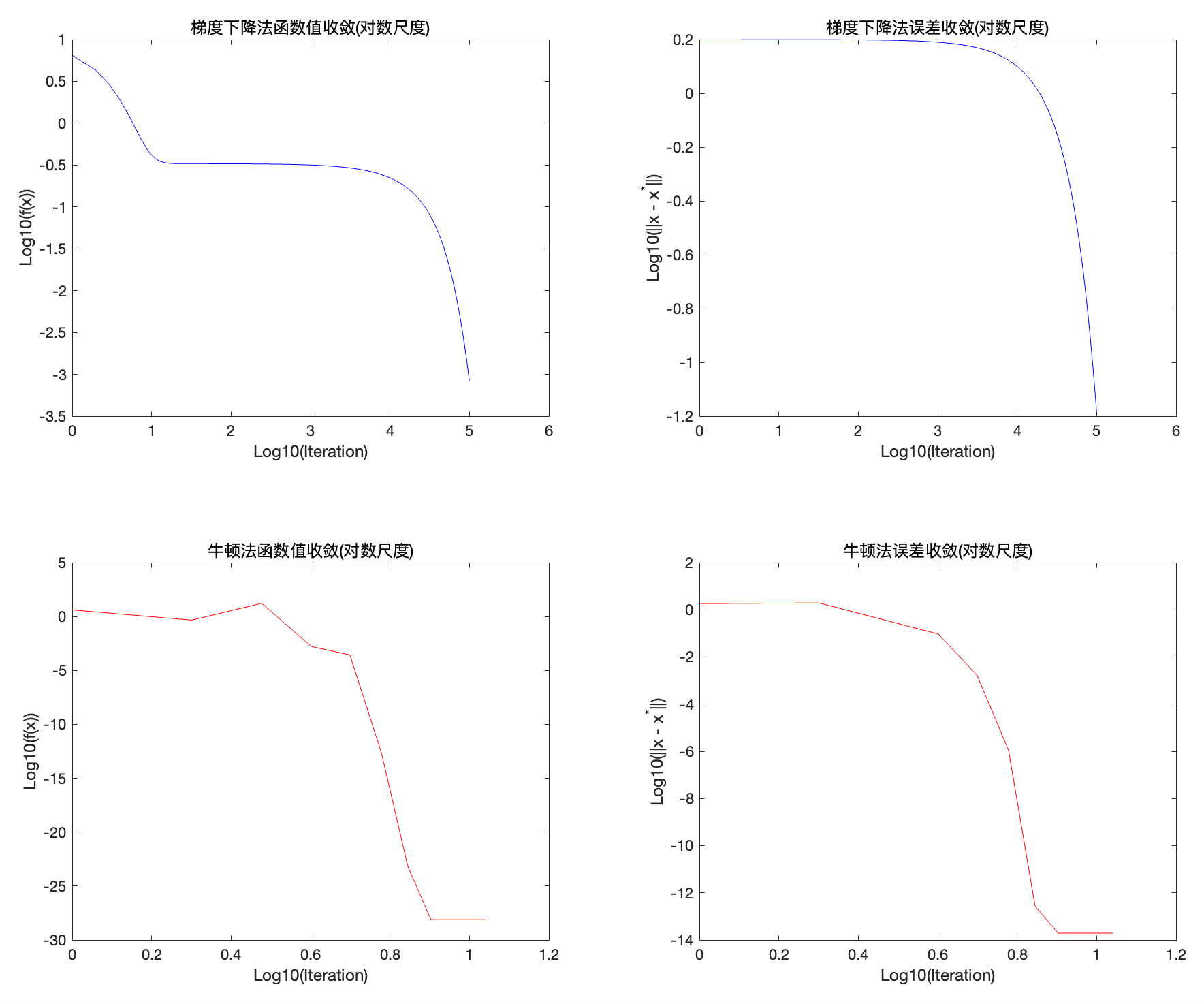

• 梯度下降法需要较多迭代才能逐渐逼近最优点，收敛速度较慢。

• 牛顿法在相对较少的迭代次数内快速降低函数值并逼近最优点，收敛速度更快。

为增强牛顿法的鲁棒性，可以使用一些方法来稳定Hessian矩阵，或者将算法与线搜索方法结合，不过还是那句话，时代变了，当模型又高纬又复杂，直接上神经网络，近似 Hessian 矩阵或其逆 H^{-1}。或者动态学习每一步的最优步长 \alpha_k，不用自己纠结选步长。

或者直接暴力一点，传统优化算法都不要了，直接学习一个端到端的优化器，它通过输入 函数的梯度或样本点，直接输出下一步的迭代结果，比如用RNN（递归神经网络）学习迭代规则：

但是一般没有足够的数据。

综上所述，梯度下降法可能收敛速度慢，步长选择要求高。此外，对于局部Convex函数，梯度下降法容易陷入局部极小值。因此，牛顿法更适合用于优化Rosenbrock这样的函数，收敛快速且精确，并且对局部Convex函数表现良好。然而，牛顿法也有局限性，即计算Hessian矩阵逆的高昂成本。

完整代码

clear all; close all; clc;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 该代码演示对Rosenbrock函数的可视化与优化求解过程。
% Rosenbrock函数定义为：
% f(x1, x2) = (1 - x1)^2 + 100*(x2 - x1^2)^2
% 此函数在点(1,1)处有全局最小值。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%% 定义Rosenbrock函数及其网格数据
f = @(x1, x2) (1 - x1).^2 + 100*(x2 - x1.^2).^2;

% 定义绘图范围
x1 = linspace(-2,2,150);
x2 = linspace(-0.5,3,150);
[X1,X2] = meshgrid(x1,x2);
F = f(X1,X2);

% 全局最优点
x_star = [1; 1];

%% 可视化：3D表面图
figure;
surf(x1,x2,F);
xlabel('X_1'); ylabel('X_2'); zlabel('f(x_1,x_2)');
shading interp; camlight; axis tight;
title('Rosenbrock函数的3D表面图');

%% 2D热度图与等高线图
% 在深入分析前，先通过热度图和等高线图对函数有更直观的认识。

% 绘制热度图（保持x2为横轴、x1为纵轴，以符合meshgrid约定）
figure;
imagesc(x2, x1, F); axis xy;            
colormap jet(256); 
colorbar;
xlabel('X_2'); ylabel('X_1');
title('Rosenbrock函数的2D热度图（x_2为横轴，x_1为纵轴）');
hold on;
% 在热度图上标注全局最优点
plot(x_star(2), x_star(1), 'r*', 'MarkerSize', 8, 'LineWidth',2);
text(x_star(2)+0.1, x_star(1)+0.1, '最优点(1,1)','Color','r','FontSize',10);
hold off;

% 绘制等高线图（以x_1为横轴，x_2为纵轴），并在图中标记最优点
figure; 
contour_levels = 10;
contour(x1,x2,F,contour_levels);
xlabel('X_1'); ylabel('X_2');
title('Rosenbrock函数等高线图（标记全局最优点）');
hold on; 
plot(x_star(1), x_star(2), '*r', 'MarkerSize',10, 'LineWidth',2);
plot([x_star(1) x_star(1)], [min(x2) max(x2)], 'r--', 'LineWidth',1.2);
plot([min(x1) max(x1)], [x_star(2) x_star(2)], 'r--', 'LineWidth',1.2);
text(x_star(1)+0.1, x_star(2)+0.1, '最优点(1,1)', 'Color','r','FontSize',10);
hold off;


%% Hessian矩阵特征值分析（验证局部最小性的充分条件）
Hj = [802 -400; -400 200];
disp('Hj的特征值:');
disp(eig(Hj));
% 特征值均为正数，说明此处Hj对应点为局部最小点（正定矩阵）

%% 定义梯度与Hessian函数，便于后续使用
gradf = @(x1, x2) [-2 + 2*x1 - 400*x1*x2 + 400*x1^3; 200*x2 - 200*x1^2];
Gradf = @(x) gradf(x(1), x(2));

hessf = @(x1, x2) [2 - 400*x2 + 1200*x1^2, -400*x1; -400*x1, 200];
Hessf = @(x) hessf(x(1), x(2));

%% 使用梯度下降法（Gradient Descent）示例
% 演示从某初始点开始的迭代路径，显示在等高线图上
figure; hold on;
contour(x2, x1, F,10);
xlabel('X_2'); ylabel('X_1');
title('梯度下降法优化路径示意图');
alpha = 1e-4;          % 步长
x0 = [1.5;2.5];        % 初始点
N = 1e5;               % 迭代次数上限
[x_path, fx_path] = descente_gradient(f, Gradf, N, alpha, x0);

% 绘制迭代点的移动轨迹
plot(x_path(2,:), x_path(1,:), 'k', 'linewidth', 1.5);
plot(x_path(2,end), x_path(1,end), 'ro', 'MarkerSize',6, 'LineWidth',2);
text(x_path(2,end)+0.05, x_path(1,end), '收敛点','Color','r','FontSize',8);
axis([-.5 3 -2 2]);
hold off;

%% 使用Newton法优化示例（并显示收敛性）
figure; hold on;
contour(x2, x1, F,10);
xlabel('X_2'); ylabel('X_1');
title('Newton法优化路径示意图');
x0 = [1.7;2.7];  % 初始点
N = 10;
[x_path_N, fx_path_N] = descente_Newton(f, Gradf, Hessf, N, x0);
plot(x_path_N(2,:), x_path_N(1,:), 'k', 'linewidth', 1.5);
plot(x_path_N(2,end), x_path_N(1,end), 'ro', 'MarkerSize',6, 'LineWidth',2);
text(x_path_N(2,end)+0.05, x_path_N(1,end), '收敛点','Color','r','FontSize',8);
axis([-.5 3 -2 2]);
hold off;

% 计算误差E
E = sqrt(sum((x_path_N - x_star).^2, 1));

% 绘制收敛性曲线（函数值与误差的对数对数图）
figure;
subplot(2,1,1);
plot(log10(1:N+1), log10(fx_path_N));
xlabel('Log10(Iteration)'); ylabel('Log10(f(x))');
title('Newton法对Rosenbrock函数收敛性（函数值）');

subplot(2,1,2);
plot(log10(1:N+1), log10(E));
xlabel('Log10(Iteration)'); ylabel('Log10(||x - x^*||)');
title('Newton法对Rosenbrock函数的误差收敛曲线');

%% 比较不同初始点对Newton法收敛路径的影响
figure; hold on;
contour(x2, x1, F,10);
plot(1, 1, '*k', 'MarkerSize', 14);
xlabel('X_2'); ylabel('X_1');
title('不同初始点下Newton法迭代路径对比');

cols = {'r', 'g', 'b'};
Xinit = {[-1.5;2.5], [1.7;2.7], [-0.3;0.85]};
N = 10;

for k = 1:length(Xinit)
    x0 = Xinit{k};
    [X_multi, f_X_multi] = descente_Newton(f, Gradf, Hessf, N, x0);
    plot(X_multi(2,:), X_multi(1,:), [cols{k} '*-'], 'MarkerSize', 8, 'linewidth', 1.5);
    text(X_multi(2,end)+0.05, X_multi(1,end), ['初始点收敛轨迹(' num2str(k) ')'], ...
        'Color',cols{k},'FontSize',8);
end
axis([-.5 3 -2 2]);
hold off;

% 在图中，黑色星号为全局最优点(1,1)。可观察不同初始点如何影响Newton迭代路径。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 以下为梯度下降法与牛顿法的对比，无需重复计算，直接使用已得到的结果：
% 梯度下降法结果：x_path, fx_path
% Newton法结果：x_path_N, fx_path_N
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 计算误差E，用于评价与全局最优点x_star的偏差
E_gd = sqrt(sum((x_path - x_star).^2, 1));
E_newton = sqrt(sum((x_path_N - x_star).^2, 1));

%% 在同一张等高线图中对比梯度下降法与牛顿法的迭代路径
figure; hold on;
contour(x2, x1, F,10);                 % 等高线
plot(x_star(2), x_star(1), '*k', 'MarkerSize',14); % 全局最优点标记

% 梯度下降法轨迹（已计算的x_path, fx_path）
plot(x_path(2,:), x_path(1,:), 'b.-', 'MarkerSize',10, 'LineWidth',1.5);

% 牛顿法轨迹（已计算的x_path_N, fx_path_N）
plot(x_path_N(2,:), x_path_N(1,:), 'ro-', 'MarkerSize',6, 'LineWidth',1.5);

xlabel('X_2'); ylabel('X_1');
title('梯度下降法 vs 牛顿法 优化路径对比');
legend('等高线','最优点','梯度下降法轨迹','牛顿法轨迹','Location','best');
hold off;

%% 对比函数值和误差的收敛过程（以对数尺度展示）
figure;

subplot(2,2,1);
plot(log10(1:length(fx_path)), log10(fx_path), 'b');
xlabel('Log10(Iteration)'); ylabel('Log10(f(x))');
title('梯度下降法函数值收敛(对数尺度)');

subplot(2,2,2);
plot(log10(1:length(E_gd)), log10(E_gd), 'b');
xlabel('Log10(Iteration)'); ylabel('Log10(||x - x^*||)');
title('梯度下降法误差收敛(对数尺度)');

subplot(2,2,3);
plot(log10(1:length(fx_path_N)), log10(fx_path_N), 'r');
xlabel('Log10(Iteration)'); ylabel('Log10(f(x))');
title('牛顿法函数值收敛(对数尺度)');

subplot(2,2,4);
plot(log10(1:length(E_newton)), log10(E_newton), 'r');
xlabel('Log10(Iteration)'); ylabel('Log10(||x - x^*||)');
title('牛顿法误差收敛(对数尺度)');

% 从图像中可见：
% - 梯度下降法需要较多迭代才能逐渐逼近最优点，收敛速度较慢。
% - 牛顿法在相对较少的迭代次数内快速降低函数值并逼近最优点，收敛速度更快。