随机变量与噪声的定义及生成

设x 是一个包含 1000 个点的随机变量，均值为 2， e 是一个包含 1000 个点的高斯白噪声。定义：

绘制y 关于x 的图像，以及\tilde{y} 关于\tilde{x} 的图像。计算x 和y 的均值及协方差矩阵。

解

均值：

协方差矩阵公式：

x^2 的均值计算：

y 的均值：

x 的方差计算：

clear all;clc;
n = 1000; % 定义点的数量为1000

e = randn(1,n);   % 生成高斯白噪声（1000个点）

x = 2 + randn(1,n);  % 生成以2为中心的随机变量x
y = 2*x.^2 + e;  % 计算目标变量y，非线性关系 2x^2 + 噪声

x_chap = x - mean(x); % 将x去中心化，使其均值为0
y_chap = y - mean(y); % 将y去中心化，使其均值为0

figure;
plot(x_chap,y_chap,'*')  % 绘制去中心化处理后的数据对 (x_chap, y_chap) 的分布图
xlabel('$\hat{x}$ (centered x)', 'Interpreter', 'latex');
ylabel('$\hat{y}$ (centered y)', 'Interpreter', 'latex');
title('Scatter plot of $\hat{y}$ versus $\hat{x}$', 'Interpreter', 'latex');


mean_x=mean(x); % 计算x的均值
mean_y=mean(y); % 计算y的均值
mean_x_chap  =mean(x_chap.^2); % 计算x去中心化后的平方均值（方差）
mean_y_chap  =mean(y_chap.^2); % 计算y去中心化后的平方均值（方差）
mean_xy_chap =mean(x_chap.*y_chap);   % 计算x去中心化和y去中心化的协方差

% 打印各统计值
fprintf('Mean of x: %f\n', mean_x); % 打印x的均值
fprintf('Mean of y: %f\n', mean_y); % 打印y的均值
fprintf('Mean of x_chap^2: %f\n', mean_x_chap); % 打印x去中心化平方的均值
fprintf('Mean of y_chap^2: %f\n', mean_y_chap); % 打印y去中心化平方的均值
fprintf('Mean of x_chap * y_chap: %f\n', mean_xy_chap); % 打印x去中心化和y去中心化的协方差

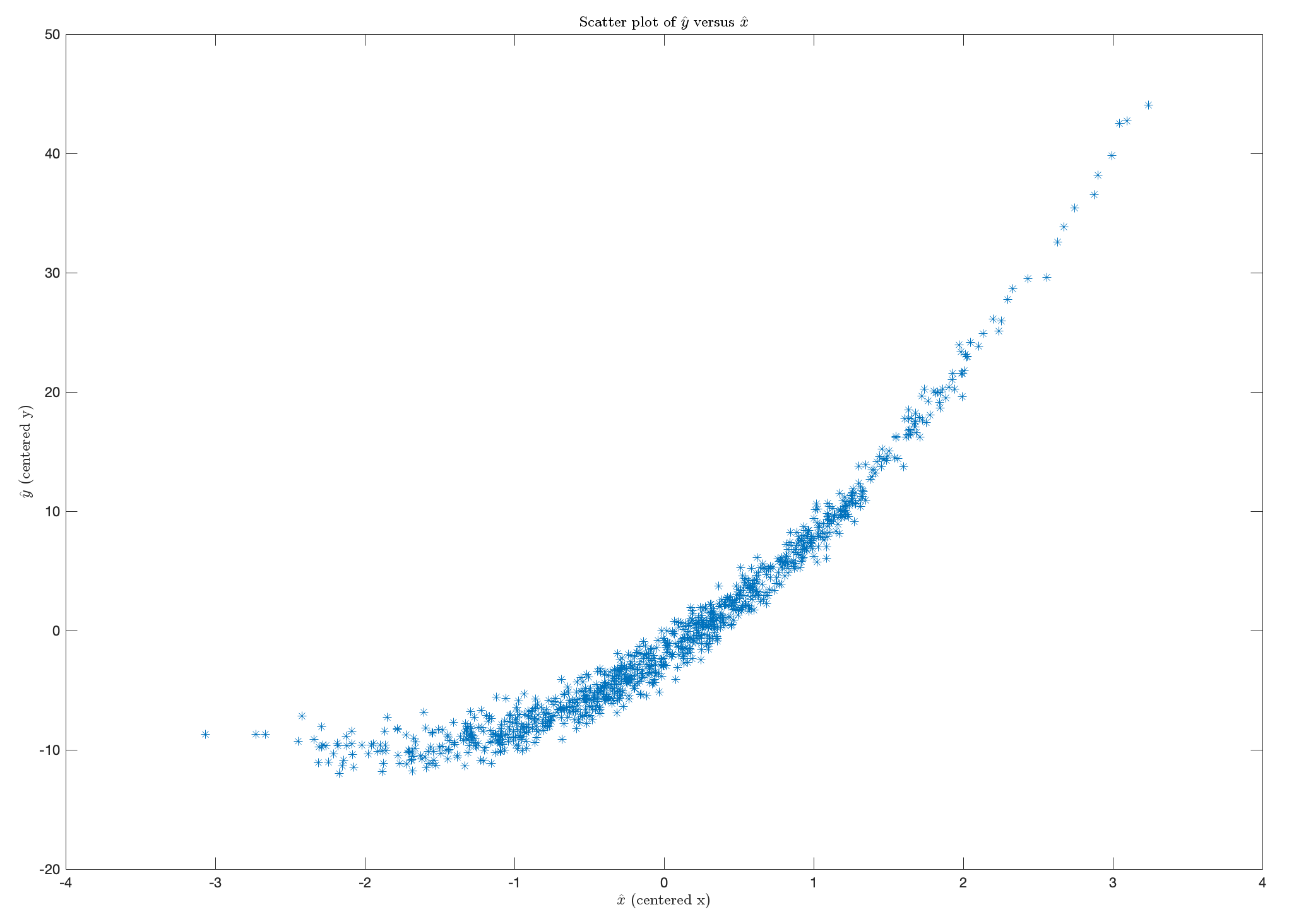
显示抛物线加噪声 的特征分布，这是由于原始的二次关系 y = 2x^2 + e 。去中心化之后，数据的分布没有改变其非线性特征，这说明数据的中心平移操作并不影响变量之间的关系。

协方差矩阵 S1 的特征值分解

计算随机矩阵 A 的协方差矩阵S1 = A \times A' ；

使用特征值分解对协方差矩阵进行处理，并重新构造矩阵 S2 ；

通过平方根矩阵的概念，进一步构造矩阵 S3 。

 %特征值的分解和特征向量的计算
clear all;clc;
A = rand(3,3);
S1 = A * A';
[R,D] = eig(S1);%对矩阵 S1 进行特征值分解，其中 R 是包含 S1 的特征向量的矩阵，而 D 是对角矩阵，其对角线上的元素是对应的特征值。
S2 = R * D * R';%使用特征向量和特征值重构矩阵 S1，确保 S2 与 S1 相同.....正交矩阵（R），逆矩阵等于转置矩阵。
A2 = sqrtm(S2);%这行代码计算矩阵 S2 的平方根，即找到一个矩阵 A2，使得 A2 * A2' = S2
S3 = A2 * A2';%验证 A2 是否确实是 S2 的平方根

A是随机生成的，不具有数学特性，A2是计算得到的平方根，因为S1 和S2都是对称、正定矩阵(由矩阵乘其转置生成)，所以其实A2也是一个对称矩阵

对 S1 的分解得到\Gamma = R \cdot D \cdot R^{-1} ，其中 D 是对角矩阵，包含 S1 的特征值，R 是正交矩阵，包含矩阵 S1 的特征向量

S1, S2, S3 是相同的矩阵（由于 S2, S3 是由 S1 的特征值和分解重构得到的）。

A \neq A2 ：因为 A 是随机的，而 A2 是对称的。

得到结果如下:

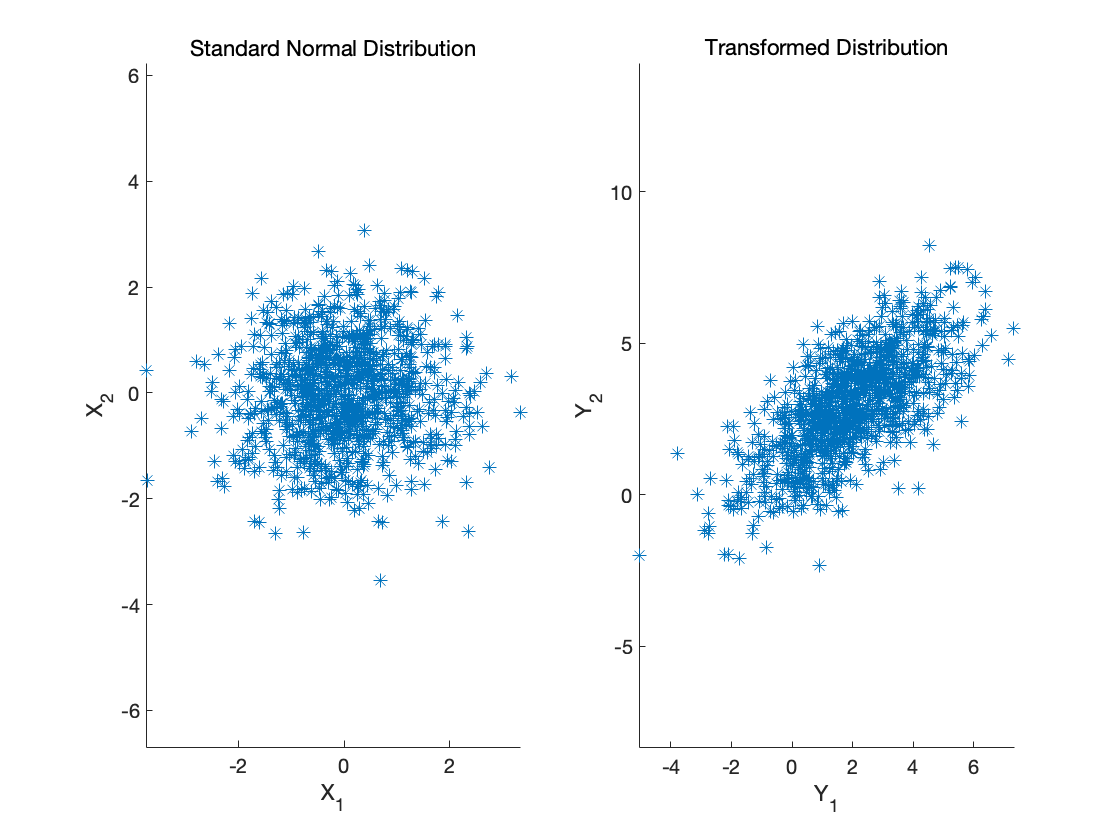
从标准正态分布生成与变换二维数据的可视化

从标准正态分布生成二维数据点，并将这些数据通过一个线性变换和偏移得到新的分布数据点，然后可视化其分布特性

% 清除工作空间和命令窗口
clear; clc;
set(0,'defaultfigurecolor','w')
% 设置参数
N = 1000; % 样本数量
Gamma_y = [3 2; 2 3]; % 协方差矩阵
ybar = [2; 3]; % 均值向量

% 生成随机二维标准正态分布数据
X = randn(2, N);

% 计算变换矩阵和偏移向量
A = sqrtm(Gamma_y); % 矩阵平方根
b = ybar; % 偏移向量

% 线性变换生成目标分布数据
Y = A * X + b;

% 绘制图像
figure;

% 子图1：标准正态分布数据散点图
subplot(1, 2, 1);
scatter(X(1, :), X(2, :), '*');
title('Standard Normal Distribution');
xlabel('X_1');
ylabel('X_2');
axis equal;

% 子图2：变换后的数据散点图
subplot(1, 2, 2);
scatter(Y(1, :), Y(2, :), '*');
title('Transformed Distribution');
xlabel('Y_1');
ylabel('Y_2');
axis equal;

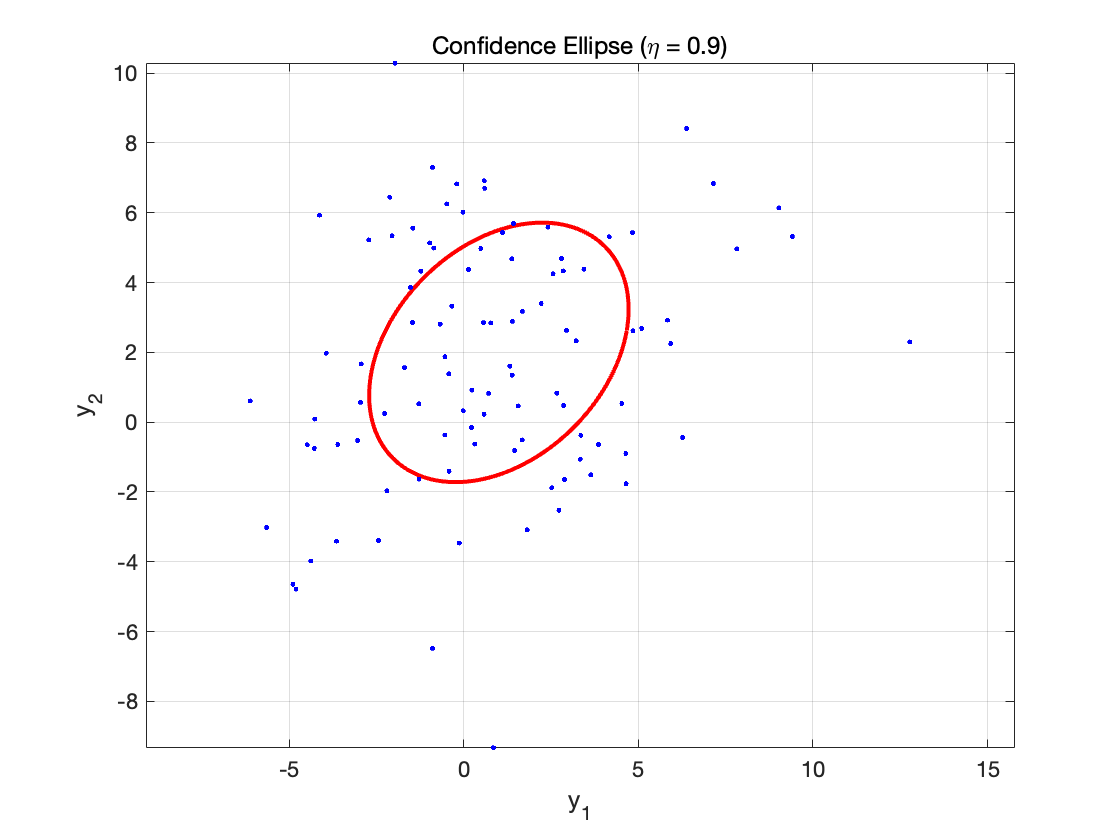
绘制高斯随机向量的置信椭圆

绘制包含高斯随机向量 y的置信椭圆 \varepsilon_y，它由概率 \eta = 0.9的随机向量 x生成。

其中w 被定义为

其中\Gamma_y 表示协方差矩阵的平方根，x 为随机向量的单位方向

椭圆

其中， s 是由\cos(\theta) 和\sin(\theta) 构成的单位圆参数化形式， \theta 为圆周角变量

% 清除工作区和命令窗口
clear; clc;

% 参数设置
N = 100; % 样本数量
ybar = [1; 2]; % 均值向量
Gy = [3, 1; 1, 3]; % 协方差矩阵
eta = 0.9; % 椭圆置信水平

% 生成单位圆上的点
s = 0:0.01:2*pi; % 参数范围
x = [cos(s); sin(s)]; % 单位圆

% 计算缩放因子
a = sqrt(-2 * log(1 - eta));

% 生成二维标准正态分布随机样本
w = randn(2, N);

% 计算协方差矩阵平方根
A = sqrtm(Gy);

% 计算随机样本和椭圆轮廓点
y = ybar + a * A * w; % 随机点变换
Y = ybar + a * A * x; % 椭圆轮廓点

% 绘图
figure;

% 绘制置信椭圆
plot(Y(1, :), Y(2, :), 'r-', 'LineWidth', 2); % 置信椭圆轮廓
hold on;

% 绘制随机点
plot(y(1, :), y(2, :), 'b.'); % 随机点

% 图形格式设置
title(['Confidence Ellipse (\eta = ', num2str(eta), ')']);
xlabel('y_1');
ylabel('y_2');
axis equal;
grid on;
hold off;

置信椭圆（预测）

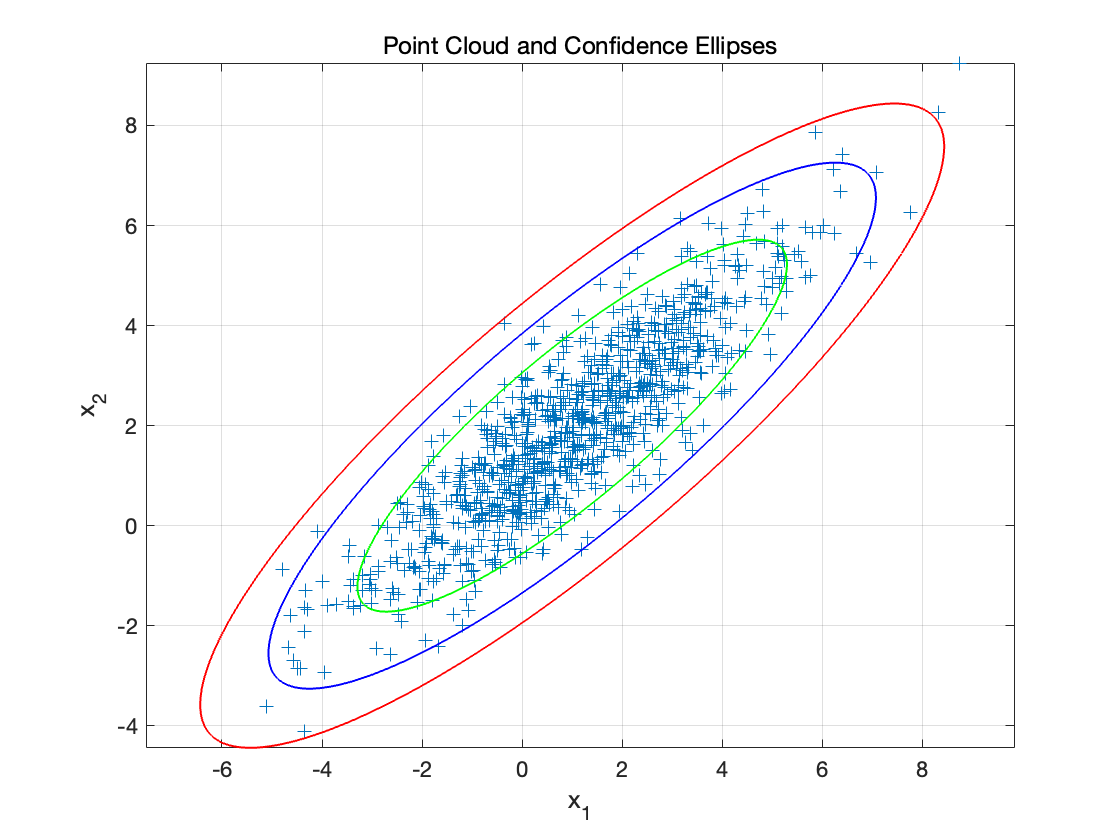
我们希望生成一个在\mathbb{R}^2 空间以零为中心、协方差矩阵为单位阵的高斯随机点云（通常记为N(0, I) 的二维高斯分布），样本数量为N=1000 个点。接着，通过线性变换和平移，将这一基础点云转化为新的高斯分布，其均值和协方差矩阵指定如下:

绘制对应于置信概率\eta \in \{0.9, 0.99, 0.999\} 的置信椭圆

% 任务 1：清除工作区并设置初始参数
clear; close all; clc;

% 参数定义
N = 1000; % 样本数量
b = randn(2, N); % 二维标准正态随机变量

Gamma = [4 3; 3 3]; % 协方差矩阵
xbar = [1; 2]; % 均值向量

A = sqrtm(Gamma); % 协方差矩阵平方根
x = xbar + A * b; % 转换为具有均值 xbar 和协方差 Gamma 的分布

% 绘制点云和置信椭圆
figure;
plot(x(1, :), x(2, :), '+'); % 点云
hold on;
draw_ellipse(xbar, Gamma, 0.9, 'g'); % 置信水平 0.9 的椭圆（绿色）
draw_ellipse(xbar, Gamma, 0.99, 'b'); % 置信水平 0.99 的椭圆（蓝色）
draw_ellipse(xbar, Gamma, 0.999, 'r'); % 置信水平 0.999 的椭圆（红色）
grid on;
title('Point Cloud and Confidence Ellipses');
xlabel('x_1');
ylabel('x_2');
axis equal;

接下来从\mathbf{x} 的点云中重新估计\bar{\mathbf{x}} 和\Gamma_{\mathbf{x}}。

%% 任务 3：从点云中估算均值和协方差矩阵
% 计算估计的均值
est_xbar = mean(x, 2);

% 计算估计的协方差矩阵
est_Gx = cov(x.');

% 显示估计结果
disp('Estimated Mean (x̄):');
disp(est_xbar);
disp('Estimated Covariance Matrix (Γ_x):');
disp(est_Gx);

得到结果如下

此分布表示我们对系统初始条件（例如一个机器人）的认识，该系统由以下形式的状态方程描述：

其中输入u(t) = \sin(t) 是已知的。编写一个程序来演示随时间的点云演变。采样周期取为\delta = 0.01 \ \mathrm{s}。

仅通过使用置信椭圆的计算来表示此演变。

%% 任务 4：动态点云及椭圆随时间变化
% 清除所有变量并关闭所有图形窗口
clear; close all;

% 参数定义
N = 1000; % 样本数量
b = randn(2, N); % 二维标准正态随机变量

Gamma = [4 3; 3 3]; % 协方差矩阵
xbar = [1; 2]; % 均值向量

A = sqrtm(Gamma); % 协方差矩阵平方根
x = xbar + A * b; % 初始点云

% 动态系统定义
A_dyn = [0 1; -1 0]; % 动态系统矩阵
B_dyn = [2; 3]; % 控制输入向量
dt = 0.01; % 时间步长
tf = 5; % 模拟总时长
time = 0:dt:tf; % 时间向量

% 初始点云
X = randn(2, N);

% 动态仿真
figure;
for t = time
    % 动态系统更新
    Ag = eye(2) + A_dyn * dt; % 离散化系统矩阵
    ug = dt * B_dyn * sin(t); % 控制输入

    X = Ag * X + ug; % 更新点云位置

    % 从点云估算均值和协方差矩阵
    est_xbar = mean(X, 2); % 估计均值
    est_Gx = cov(X.'); % 估计协方差矩阵

    % 绘制点云及置信椭圆
    clf();
    plot(X(1, :), X(2, :), '+'); % 动态点云
    hold on;
    draw_ellipse(est_xbar, est_Gx, 0.999, 'g'); % 绘制置信椭圆（置信水平 0.999）
    title(['Dynamic Point Cloud and Confidence Ellipse at t = ', num2str(t)]);
    xlabel('x_1');
    ylabel('x_2');
    axis equal;
    grid on;
    drawnow;
end

协方差矩阵的传播

我们考虑三个随机向量\mathbf{a}、 \mathbf{b} 和\mathbf{c}，它们以零为中心，协方差矩阵等于单位矩阵。这三个向量相互独立。定义两个随机向量如下：

其中\mathbf{A} 和\mathbf{C} 是已知矩阵。

首先来给出这些随机向量的数学期望\bar{\mathbf{x}} 和\bar{\mathbf{y}} 及其协方差矩阵\Gamma_{\mathbf{x}} 和\Gamma_{\mathbf{y}} 的表达式，作为\mathbf{A} 和\mathbf{C} 的函数。

由于\mathbf{a},\mathbf{b},\mathbf{c} 都是零均值且相互独立，计算期望相对简单：

接下来求协方差矩阵时会用到这些性质。由于独立性和零均值，会有许多项被消去，从而得到较为简洁的形式：

下面是对\Gamma_{\mathbf{x}} 的详细推导过程，先将定义写出，然后逐步利用零均值和独立性化简：

上述表达式中有多项可以化简:

因为:

因此上式中相关项为零：

又因为:

所以最终有：

类似地，对于\Gamma_{\mathbf{y}} 的计算，我们同样从定义出发，利用\mathbf{y} = \mathbf{C}\mathbf{x} + \mathbf{c} 展开期望，并用已知的零均值和独立性条件消去交叉项： 

 由于\mathbb{E}[\mathbf{x}\mathbf{c}^\top]=0，且\Gamma_{\mathbf{c}} = \mathbf{I}，将这些代入后:

构造向量\mathbf{v} = (\mathbf{x}, \mathbf{y})。计算向量\mathbf{v} 的数学期望\bar{\mathbf{v}} 和协方差矩阵\Gamma_{\mathbf{v}}。

定义联合向量：（这里我们将\mathbf{x} 和\mathbf{y} 堆叠成一个更高维的向量\mathbf{v}，以便处理联合协方差）

 协方差矩阵可以写成分块矩阵形式，其中对角块为各自的协方差，非对角块为互协方差：

 利用上一步中的结果直接填入：

 接下来需要求出\mathbb{E}[\mathbf{x} \mathbf{y}^\top] 和\mathbb{E}[\mathbf{y} \mathbf{x}^\top]，为此我们将\mathbf{y} 展开并利用独立性：（将\mathbf{y} 替换为\mathbf{C}\mathbf{x} + \mathbf{c}，再求相应期望）

由于\mathbb{E}[\mathbf{x}\mathbf{c}^\top] = 0，故：

 同理对称地有：

从上一步推导随机向量\mathbf{z} = \mathbf{y} - \mathbf{x} 的协方差矩阵。假设\mathbf{x} 和\mathbf{y} 的维度相同。

现在考虑定义\mathbf{z} = \mathbf{y} - \mathbf{x}： （利用刚才的结果，为新定义的向量\mathbf{z} 求协方差矩阵）

因为\bar{\mathbf{y}}=0 和\bar{\mathbf{x}}=0，有：

展开后：

将之前求得的期望代入：

因此可以将这些项代回到\Gamma_{\mathbf{z}} 中以得到最终结果。

 对\mathbf{y} 进行一次测量，因此此随机向量变为确定性向量，并完全已知。使用线性、非偏和正交估计器，给出\mathbf{x} 的估计值\hat{\mathbf{x}}。

 测量后\mathbf{y} 不再是随机量，我们使用最优线性无偏估计方法(LMMSE)：

因为\bar{\mathbf{x}} = 0, \bar{\mathbf{y}} = 0：

增益矩阵\mathbf{K} 为：

代入各个矩阵的定义即可得到：

摆线

一个点放置在一个轮子上 沿着如下形式的参数方程 摆线运动：

其中， x 对应于质量的横坐标， y 对应于质量的高度。 测量了不同时间点t 下的y 值，根据这些数据，我们希望估计参数p_1 和p_2

测量误差具有10\ \mathrm{cm} 的标准差。使用非偏正交滤波器，计算p_1 和p_2 的估计值。

给出观测向量\mathbf{y} 和参数向量\mathbf{p} 之间的关系，以及噪声项\boldsymbol{\beta}

对于线性非偏最优估计 类似于 LMMSE 问题，一般估计形式为：估计量 = 先验均值 + 增益矩阵 * (观测偏差)

我们假设先验参数均值\bar{\mathbf{p}} 为零向量，同时给出参数先验协方差矩阵\Gamma_{\mathbf{p}} :

这里的\Gamma_{\mathbf{p}} 表示参数的先验不确定性较大， 10^4 可理解为某种标度上的较大方差，以表示我们对p_1, p_2 的初始估计非常不确定

下一步是计算观测向量\mathbf{y} 的协方差矩阵\Gamma_{\mathbf{y}}。由于\mathbf{y} 是由\mathbf{C}\mathbf{p} 和噪声\boldsymbol{\beta} 构成，那么\Gamma_{\mathbf{y}} 就可由参数先验协方差和噪声协方差传播而来:

在已知观测误差\Gamma_{\boldsymbol{\beta}} 的情况下，我们通过上述公式获得\Gamma_{\mathbf{y}}。有了\Gamma_{\mathbf{y}}，就可以构建增益矩阵\mathbf{K}。

增益矩阵\mathbf{K} 的定义采用最小方差估计准则 :

上式中， \Gamma_{\mathbf{y}}^{-1} 为观测不确定性的逆矩阵，它会权衡参数的不确定性与测量数据所携带的信息，以确定如何更新参数估计。

最后，我们可以计算更新后的参数不确定性，即误差协方差矩阵\Gamma_{\boldsymbol{\varepsilon}}

该结果显示，利用观测数据更新参数后，参数的后验不确定性会降低。这里\Gamma_{\boldsymbol{\varepsilon}} 表示参数估计误差的最终方差。当观测数据质量 相对于噪声水平 较好时，该方差应显著小于初始先验方差。

% 清理工作区并初始化
close all; clc;

% 已知测量数据
t = [1; 2; 3; 7]; % 时间点 (s)
y = [0.38; 3.25; 4.97; -0.26]; % 高度数据 (m)

% 构造观测矩阵 C
C = [ones(size(t)), -cos(t)]; % 矩阵 [1, -cos(t)]

% 参数初始化
pbar = zeros(2, 1); % 参数估计初值
GammaP = 1e4 * eye(2); % 参数协方差初值
GammaB = (0.1)^2 * eye(length(t)); % 测量噪声协方差矩阵

% 计算总噪声协方差矩阵
GammaY = C * GammaP * C' + GammaB;

% 卡尔曼增益计算
K = GammaP * C' / GammaY;

% 更新协方差矩阵
GammaEpsilon = GammaP - K * C * GammaP;

% 残差计算
ytild = y - C * pbar;

% 更新参数估计
Phat = pbar + K * ytild;

% 打印估计参数
disp('估计的参数值:');
disp(['p1 = ', num2str(Phat(1))]);
disp(['p2 = ', num2str(Phat(2))]);

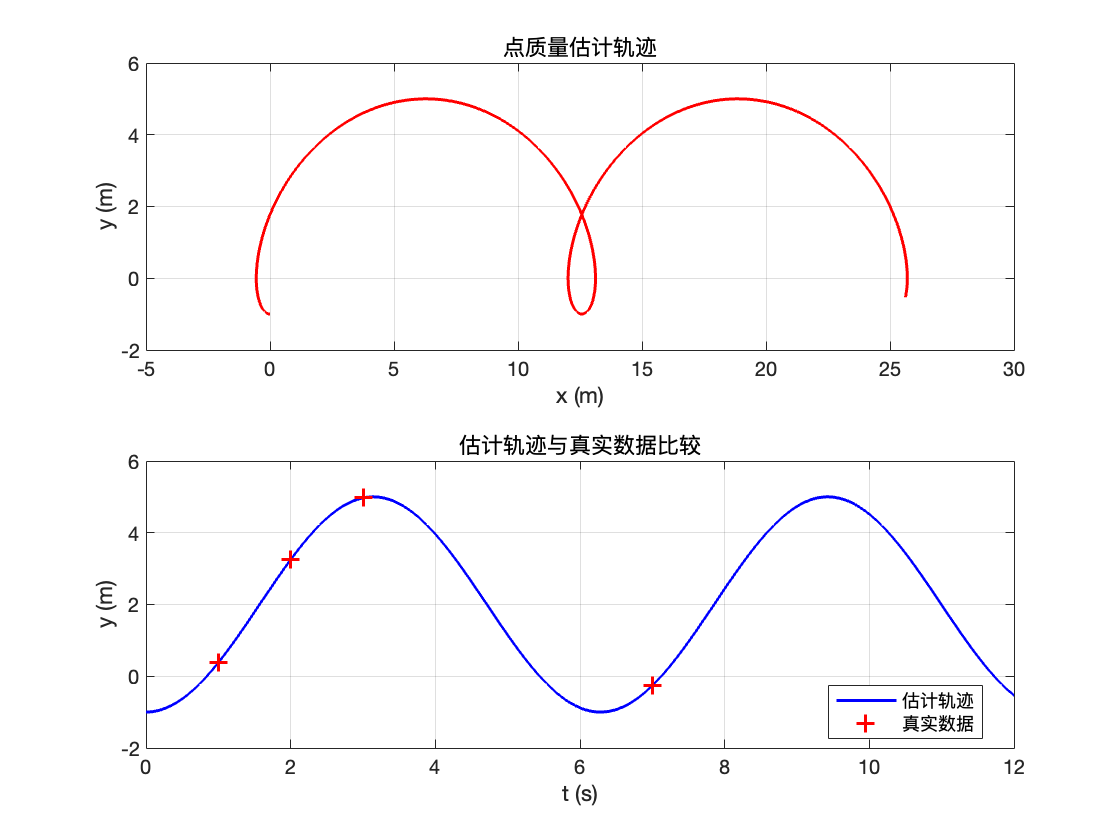
 绘制点质量的估计轨迹（ x 和y）并同时绘制y 的轨迹，将真实数据叠加于上。

% 模拟轨迹生成
ta = 0:0.01:12; % 模拟时间范围
x1 = Phat(1) * ta - Phat(2) * sin(ta); % x 轨迹
y1 = Phat(1) - Phat(2) * cos(ta); % y 轨迹

% 绘图：摆线轨迹
figure;
subplot(2, 1, 1);
plot(x1, y1, 'r', 'LineWidth', 1.5); hold on;
xlabel('x (m)'); ylabel('y (m)');
title('点质量估计轨迹');
grid on;

% 绘图：y 轨迹与真实数据比较
subplot(2, 1, 2);
plot(ta, y1, 'b', 'LineWidth', 1.5); hold on;
plot(t, y, 'r+', 'MarkerSize', 8, 'LineWidth', 1.5);
xlabel('t (s)'); ylabel('y (m)');
legend('估计轨迹', '真实数据', 'Location', 'Best');
title('估计轨迹与真实数据比较');
grid on;

解三元一次方程

线性估计器可以用于解决可转化为线性方程的问题。我们从一个简单的线性系统出发，通过调用三次Kalman滤波器并借助Matlab实现对其进行求解，从而得到参数的最优估计值与误差协方差矩阵。考虑以下系统：

在这个问题中我们需要处理的系统是一个三元一次方程组，并且引入了测量噪声。参数的初始估计可以设为零，并给定其初始不确定性。测量噪声协方差矩阵是已知的，通过Kalman滤波器的更新过程，我们将测量信息不断纳入到估计中，最终得到参数的后验估计。

首先有一个初始状态估计向量和初始状态协方差矩阵。利用测量数据构成的矩阵C以及噪声协方差矩阵Gamma_beta计算出S。接着依据Kalman滤波器的标准公式计算增益矩阵K。然后在得到修正后的参数估计值和更新后的误差协方差矩阵之后，我们用它们对下一个时刻的状态和协方差进行预测并再次进行相同步骤的更新。通过重复这一过程三次，可以有效降低参数估计的不确定性。

下面是公式

这个公式给出了测量创新的协方差S。它是由先验参数不确定性经由矩阵C传播到测量空间后加上测量噪声协方差Gamma_beta得到的。

此处K为Kalman增益，它决定了参数估计对新测量信息的依赖程度。当测量噪声较小或先验不确定性较大时K会较大，这表示参数估计会更多地依靠新观测进行修正。

上式为创新向量，它是实际测量值与根据当前参数估计预测出的测量值之差。

利用创新向量和Kalman增益，我们对参数进行更新获得后验估计值。

更新后的误差协方差为原先的协方差减去通过新信息修正的部分，体现了参数不确定性的降低。

这是对下一个时刻状态进行预测的公式。在此问题中若无额外状态传递则可将A视为恒等矩阵，u为可能的控制输入项。

这里根据状态方程更新下一个时刻的误差协方差，G_alpha是过程噪声协方差。

这是一个给定的初始条件，它表示在新的条件下参数协方差可以根据需要初始化为一个零矩阵或其他值。

这是测量噪声协方差矩阵，根据该矩阵我们能够明确每个观测方程所携带的噪声特性，从而在更新时正确权衡测量信息的可信程度。

这是参数初始估计值的设定，表示在没有任何先验信息时我们对参数值的初步假设可为零。

通过以上步骤反复调用Kalman滤波器三次，借助Matlab进行数值求解，我们最终就能获得参数的后验估计值以及对应的误差协方差矩阵。这样一来即使存在测量噪声，也能在一定程度上实现参数的精确估计，从而有效解决该三元一次方程系统的求解问题。

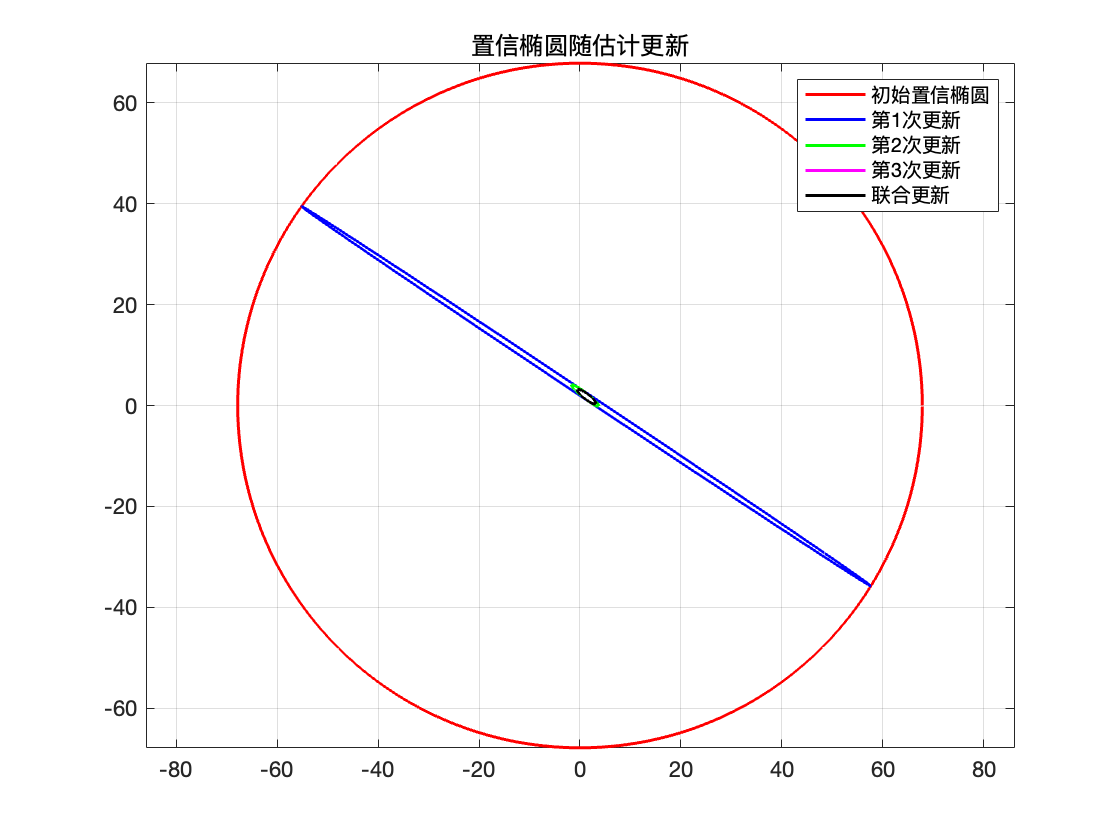
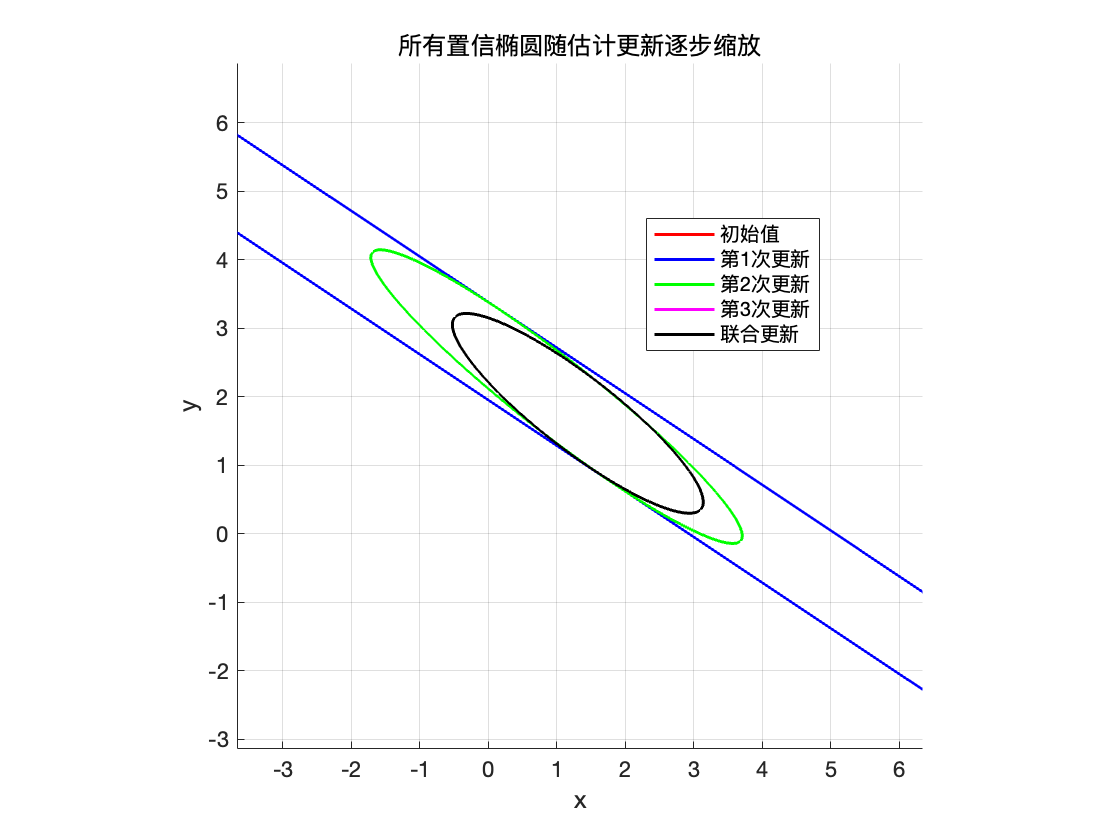
绘制每次调用对应的置信椭圆。

% 清理工作区并初始化
clear all;
clc;
close all;

% 系统参数
Galpha = zeros(2, 2); % 过程噪声协方差
A = eye(2); % 状态转移矩阵
C0 = [2, 3]; % 第一方程系数
C1 = [3, 2]; % 第二方程系数
C2 = [1, -1]; % 第三方程系数
u = 0; % 输入
xhat0 = [0; 0]; % 初始状态估计
Gx0 = 1e3 * eye(2); % 初始协方差
y = [8; 7; 0]; % 测量值
Gbeta = diag([1, 4, 4]); % 测量噪声协方差矩阵
C = [C0; C1; C2]; % 联合观测矩阵

% 各步更新结果存储
steps = {}; % 存储每一步的估计值和协方差
colors = {'r', 'b', 'g', 'm', 'k'}; % 每次更新不同颜色

% 第一次更新
[xhat1, Gx1] = kalman(xhat0, Gx0, u, 8, Galpha, 1, A, C0);
steps{1} = struct('xhat', xhat0, 'Gx', Gx0); % 初始值
steps{2} = struct('xhat', xhat1, 'Gx', Gx1);

% 第二次更新
[xhat2, Gx2] = kalman(xhat1, Gx1, u, 7, Galpha, 4, A, C1);
steps{3} = struct('xhat', xhat2, 'Gx', Gx2);

% 第三次更新
[xhat3, Gx3] = kalman(xhat2, Gx2, u, 0, Galpha, 4, A, C2);
steps{4} = struct('xhat', xhat3, 'Gx', Gx3);

% 联合更新
[xhat_final, Gx_final] = kalman(xhat0, Gx0, u, y, Galpha, Gbeta, A, C);
steps{5} = struct('xhat', xhat_final, 'Gx', Gx_final);

% GIF 动画参数
filename = 'multi_ellipse_zoom.gif'; % 输出 GIF 文件名
num_frames = 50; % 动画帧数
frame_pause = 0.1; % 每帧间隔时间 (秒)

% 生成动画
for i = 1:num_frames
    % 缩放范围逐渐变小
    scale = 80 - (75 / (num_frames - 1)) * (i - 1); % 缩放范围从 80 到 5
    clf;
    hold on;
    axis equal;
    grid on;
    
    % 绘制所有置信椭圆
    for j = 1:length(steps)
        draw_ellipse(steps{j}.xhat, steps{j}.Gx, 0.9, colors{j}, 1.5);
    end
    
    % 设置轴范围
    axis([-scale, scale, -scale, scale]);
    title('所有置信椭圆随估计更新逐步缩放');
    xlabel('x'); ylabel('y');
    grid on;
    legend({'初始值', '第1次更新', '第2次更新', '第3次更新', '联合更新'}, 'Location', 'Best');
    drawnow;
    
    % 将当前帧保存到 GIF
    frame = getframe(gcf);
    im = frame2im(frame);
    [imind, cm] = rgb2ind(im, 256);
    if i == 1
        imwrite(imind, cm, filename, 'gif', 'Loopcount', inf, 'DelayTime', frame_pause);
    else
        imwrite(imind, cm, filename, 'gif', 'WriteMode', 'append', 'DelayTime', frame_pause);
    end
end

disp(['GIF 动画已保存为: ', filename]);

基于到墙壁距离测量的定位

问题描述

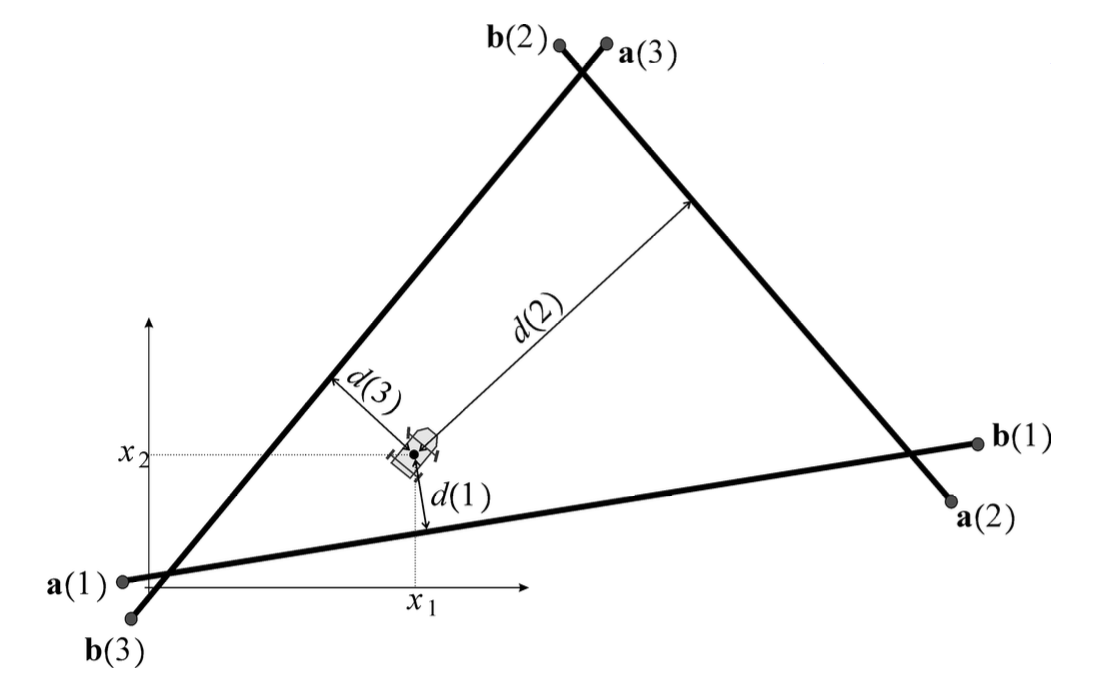
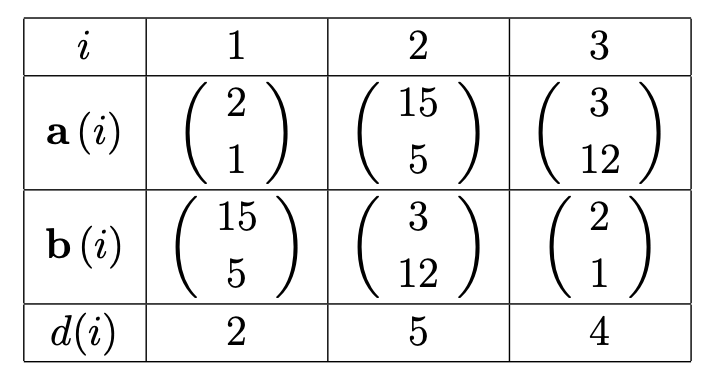
我们考虑一个假设为点的机器人，其位置为x = (x_1, x_2)。它通过测量到三个墙的距离来确定位置，如下图所示。第i 面墙由两个点a(i) 和b(i) 确定的直线表示。

机器人到第i 墙的距离定义为：

其中

每个距离的测量值都带有一个误差\beta_i，该误差是中心化的，具有单位方差，并且所有误差彼此独立。在进行任何测量之前，机器人认为它的位置为\bar{x} = (1, 2)，并且假设与之相关联的协方差矩阵为100 \cdot I。

要求：根据a(i)、 b(i) 和d(i) 的数据，估计机器人的位置，以及基于无偏线性正交估计器，计算误差的协方差矩阵。

理论计算

我们可以将观测数据和状态参数之间的关系转化为简单的线性方程形式。首先定义

将其中的向量展开，可以写为

利用行列式的性质将其展开为

行列式的计算结果为

接下来我们将上述关系整理出类似于y_i = C_i x_i + \beta_i 的形式。

通过代入并整理项可得到

将常数项移到左侧

可以将右侧写为向量与状态变量的内积

记左侧为新的观测量

在这里可以定义

这样就得到了线性化的观测方程, 它与状态变量和噪声之间的关系清晰可见。这个过程为后续利用卡尔曼滤波器进行估计奠定了基础。通过适当地构造矩阵C和向量y, 并结合噪声协方差矩阵, 就可以搭建卡尔曼滤波所需的关键参数。

当完成这些理论计算之后, 就可以编写MATLAB代码来使用卡尔曼滤波器对系统参数进行求解。在代码中会先定义初始参数的先验估计与协方差矩阵, 然后利用更新方程融合测量数据, 最终得到最优的后验参数估计和误差协方差。

代码实现

clear all; clc;close all

%% 参数定义
% 定义墙壁端点的坐标
a = [2 15 3;
     1 5 12];  
b = [15 3 2;
     5 12 1];  

% 三个测量得到的距离
d = [2; 5; 4]; 

% 初始状态与协方差
xbar = [1; 2];
G0 = 100 * eye(2);

% 状态转移矩阵与过程噪声（本例设A为单位阵，无输入无过程噪声）
A = eye(2);
u1 = 0; 
Galpha = 0;

% 测量噪声协方差矩阵
Gbeta = eye(3);

% 根据给定墙壁与测量计算矩阵C和偏移量d2
C = zeros(3,2);
d2 = zeros(3,1);
for i = 1:3
    u = (b(:, i) - a(:, i)) / norm(b(:, i) - a(:, i));
    C(i, :) = [-u(2), u(1)];
    d2(i) = [a(2, i), -a(1, i)] * u;
end

% 合成观测向量
y = d + d2;

%% 简单实现：传统的三次单独测量更新
% 在此部分中，我们进行三次卡尔曼滤波更新，每次使用一个测量值
% 并在每次更新后绘制位置置信椭圆。
figure; 
% 绘制墙壁
plot([2, 15], [1, 5], 'black', 'LineWidth', 2); hold on;
plot([15, 3], [5, 12], 'black', 'LineWidth', 2); hold on;
plot([3, 2], [12, 1], 'black', 'LineWidth', 2); hold on;
axis equal;

% 第一次单独测量更新
[x1, G1, xup1, Gup1] = kalman(xbar, G0, u1, y(1), Galpha, Gbeta(1,1), A, C(1,:));
draw_ellipse(xup1, Gup1, 0.9, 'g', 1.5); hold on;

% 第二次单独测量更新
[x2, G2, xup2, Gup2] = kalman(x1, G1, u1, y(2), Galpha, Gbeta(2,2), A, C(2,:));
draw_ellipse(xup2, Gup2, 0.9, 'r', 1.5); hold on;

% 第三次单独测量更新
[x3, G3, xup3, Gup3] = kalman(x2, G2, u1, y(3), Galpha, Gbeta(3,3), A, C(3,:));
draw_ellipse(xup3, Gup3, 0.9, 'b', 1.5); hold on;

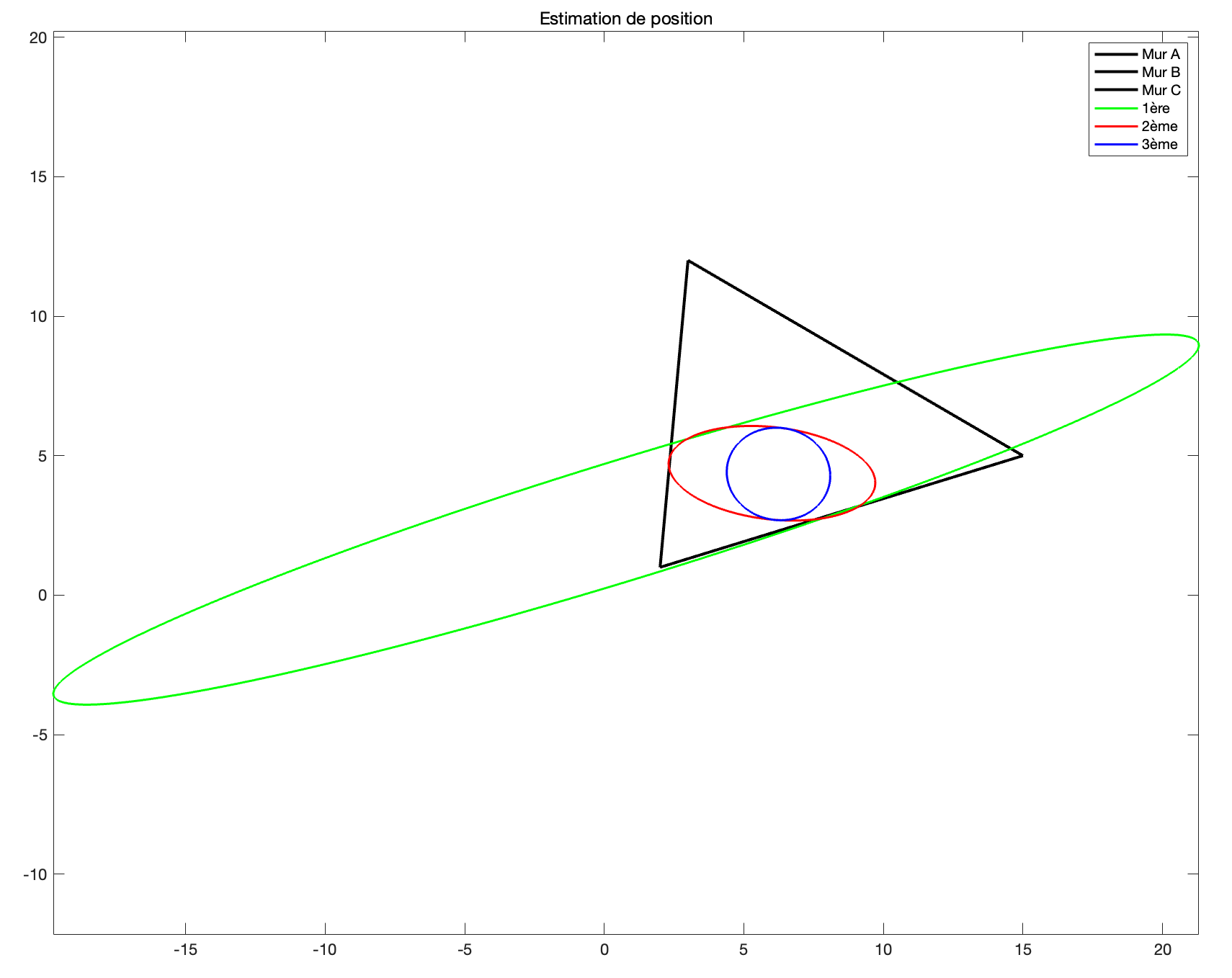
title('依次使用三个测量进行三次更新');
legend({'墙壁A','墙壁B','墙壁C','第1次更新','第2次更新','第3次更新'}, 'Location', 'northeast');

function draw_ellipse(wbar,Gw,eta,color,linewidth)
% 绘制置信椭圆函数
if (nargin<5), linewidth=1; end
if (nargin<4), color='black'; end
s = 0:0.01:2*pi;
a = sqrt(-2*log(1-eta));
w = wbar+a*sqrtm(Gw)*[cos(s); sin(s)];
plot(w(1,:), w(2,:),color,'LineWidth',linewidth)
end

function [x1, G1, xup, Gup] = kalman(x0, G0, u, y, Galpha, Gbeta, A, C)
% 卡尔曼滤波更新函数
% 此函数可同时处理标量测量和向量测量。
S = C * G0 * C' + Gbeta;
K = G0 * C' / S;  % 使用/代替inv()提高数值稳定性
ytilde = y - C * x0;
xup = x0 + K * ytilde;  
Gup = G0 - K * C * G0;
x1 = A * xup + u;
G1 = A * Gup * A' + Galpha;
end

%% 常规实现：将三个测量合并为一个三维观测向量进行一次更新
% 在此部分中，将三个测量同时用于一次卡尔曼滤波更新。
figure;
% 绘制墙壁
plot([2, 15], [1, 5], 'black', 'LineWidth', 2); hold on;
plot([15, 3], [5, 12], 'black', 'LineWidth', 2); hold on;
plot([3, 2], [12, 1], 'black', 'LineWidth', 2); hold on;
axis equal;

% 一次性使用三个测量进行更新
[x1_comb, G1_comb, xup_comb, Gup_comb] = kalman(xbar, G0, u1, y, Galpha, Gbeta, A, C);
draw_ellipse(xup_comb, Gup_comb, 0.9, 'g', 1.5); hold on;

title('一次性使用三个测量进行单次更新');
legend({'墙壁A','墙壁B','墙壁C','一次性更新结果'}, 'Location', 'northeast');

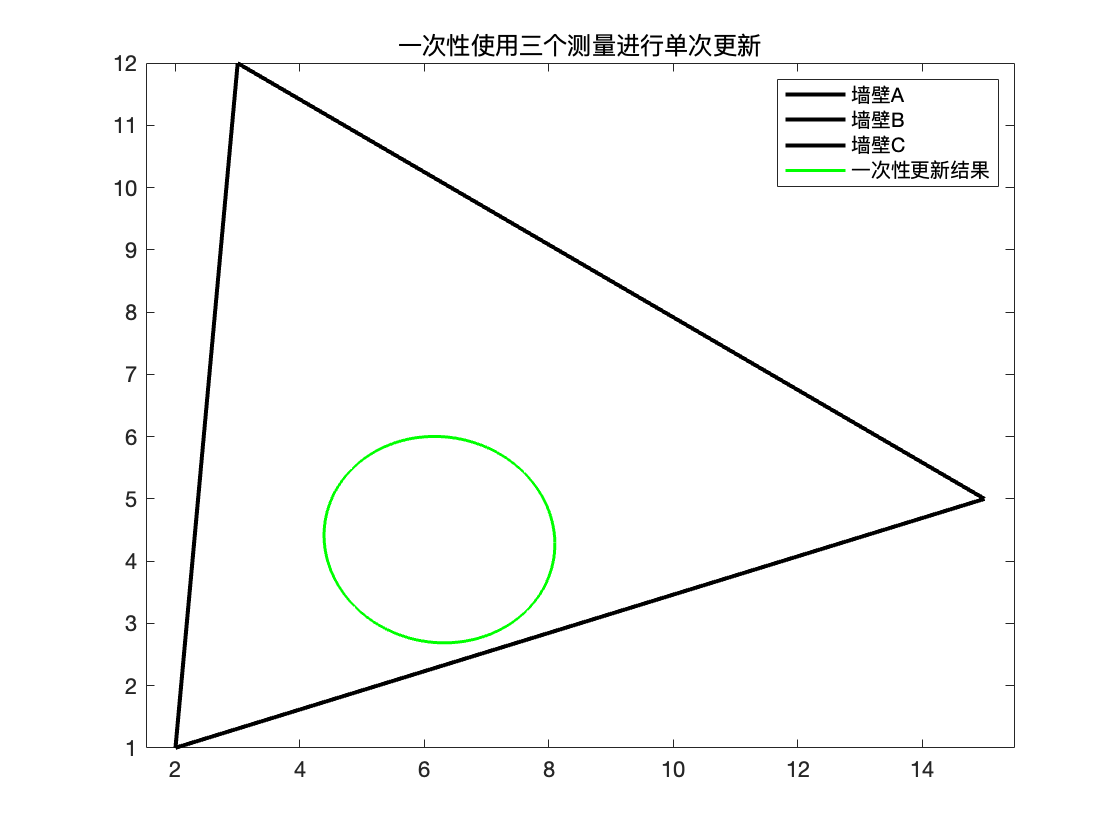在代码中，在初始化变量之后，我们首先绘制了墙壁。然后，利用理论上计算的线性表达式，我们可以计算y(i) 和C(i)。接下来，使用卡尔曼滤波器进行了三次更新，每次更新使用在上一次更新中获得的参数。最后，通过绘制置信椭圆，可以观察到第一次对汽车位置的迭代并不精确，但第三次对汽车位置的迭代已经相当精确。

我们得到的最终位置x 是：

计算得到的误差协方差矩阵是：