zehua

Zehua

惯性导航

信号处理
15
0
2025-01-25

主要针对车辆在局部切平面中的惯性导航，实现一个简化的IRS机理。我们先对2D 情况下（简化）的IRS机理进行分析，最后讨论如何开发GPS/IRS融合方案来提高导航精度。

背景介绍

主要针对车辆在局部切平面中的惯性导航，实现一个简化的IRS机理。我们先对2D 情况下（简化）的IRS机理进行分析，最后讨论如何开发GPS/IRS融合方案来提高导航精度。在惯性导航中，我们利用加速度计和陀螺仪的输出数据来计算（积分）车辆在二维局部切平面（LTP）中的运动状态（位置、速度和航向角）

我们在汽车中安装了一个GPS接收机（车内）和IMU（车顶），为了简化忽略一些元素，比如说两设备之间的杠杆臂等等。因此该汽车绕着大楼转了三圈，行驶轨迹如下:

下面我们进行坐标系的定义，首先车辆坐标系是 b-坐标系，航向坐标系是局部切平面（NED 坐标系），IMU平台坐标系是 p-坐标系，是一个 NWU 坐标系（北-西-上），坐标系这块我不懂，具体的不再展开。

放置的传感器精度有限，假设其测量误差主要由噪声和偏置引起，因此测量模型可以建模为如下形式:

\underbrace{\tilde{f}^p(t)}_{\text{加速度计测量值}} \;=\; \underbrace{f^p(t)}_{\text{真实加速度}} \;-\; \underbrace{b_f(t)}_{\text{加速度计偏置}} \;-\; \underbrace{n_f(t)}_{\text{噪声项}}
\underbrace{\tilde{\omega}^p(t)}_{\text{陀螺仪测量值}} \;=\; \underbrace{\omega^p(t)}_{\text{真实角速度}} \;-\; \underbrace{b^\omega(t)}_{\text{陀螺仪偏置}} \;-\; \underbrace{n^\omega(t)}_{\text{噪声项}}

我们根据不知道哪里来的定义，反正真实加速度和真实角速度可以写成 f^p(t) = f_{b/i}^p(t) 和\omega^p(t) = \omega_{b/i}^p(t) 的形式。

与此同时，测量偏置项可以被假设成一阶马尔可夫过程，如下:

b^\omega(t) = -\frac{1}{\tau_\omega}\, b^\omega(t) + n^{b^\omega}(t) \quad\text{且}\quad n^{b^\omega}(t)\sim N\bigl(0,\sigma_{b_\omega}\bigr)
b^f(t) = -\frac{1}{\tau_f}\, b^f(t) + n^{b^f}(t) \quad\text{且}\quad n^{b^f}(t)\sim N\bigl(0,\sigma_{b_f}\bigr)

最后 , ​ n^\omega 和 n^f是测量噪声，同样被假设为高斯白噪声，如下:

n^\omega(t)\sim N\bigl(0,\sigma_\omega\bigr), \quad n^f(t)\sim N\bigl(0,\sigma_f\bigr)

综上所属我们已经数学建模了测量模型，接下来我们正式开始第一部分 2D IRS车辆机理分析

地面车辆的 2D 简化 IRS 机理

这部分使用的是简化的方法，适用于没有钱买高精度传感器的时候，因此低成本的惯性传感器使用一个加速度计和一个陀螺仪，我们就在这个穷苦条件下分析。

首先我们对IMU测量做两个简化符号假设:

  • 沿着车辆前进方向 x^b 的加速度计测量量记为 f_{IMU}^b(x)

  • 沿着垂直方向 z^b 的陀螺仪测量量记为 \omega_{IMU}^b(z)

我们加载数据，运行代码，得到三个 IMU 测量结果图像:

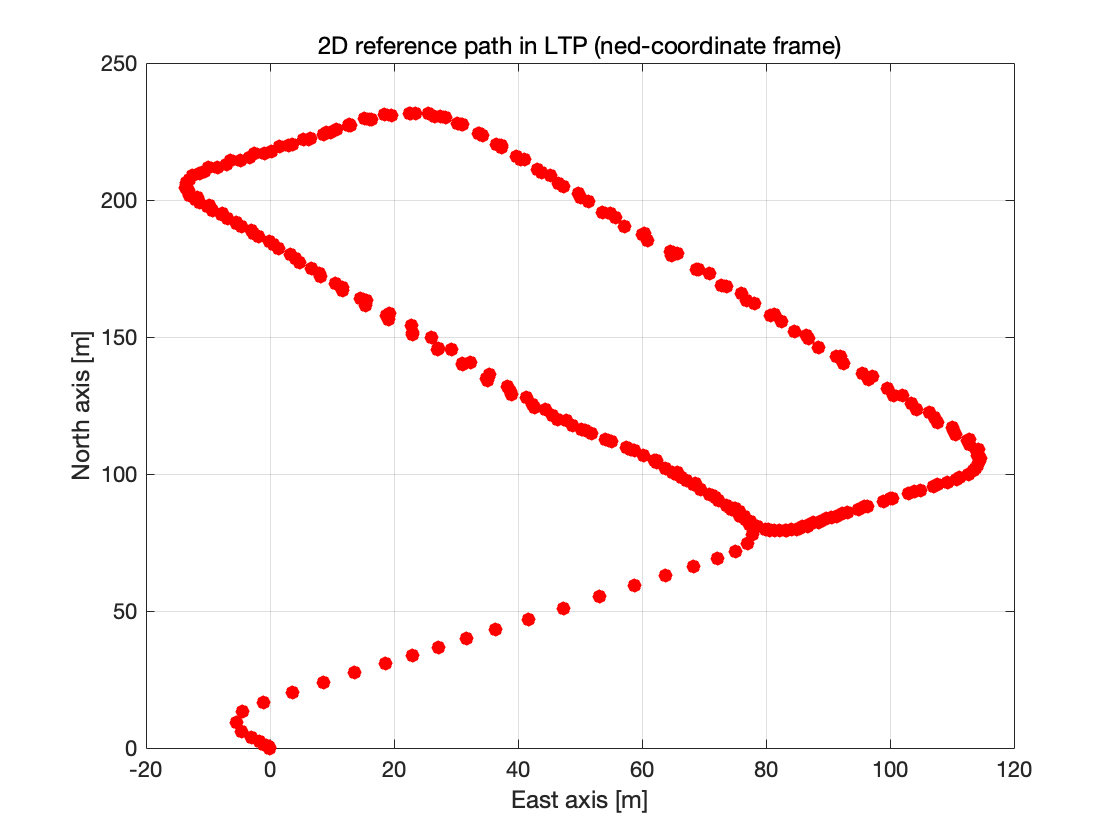
图 1：车辆行驶轨迹

这张图代表了车辆的二维平面轨迹:

  • 我们观察到车辆绕建筑物闭合行驶，这和之前绕建筑物三圈的真实情况一致。

  • 同时车辆轨迹的起始点从 (0, 0)开始，这是因为LTP 是以轨迹起点为原点定义的。

  • 轨迹拐弯处较平滑，说明导航系统很好的捕捉到了车辆的旋转特性

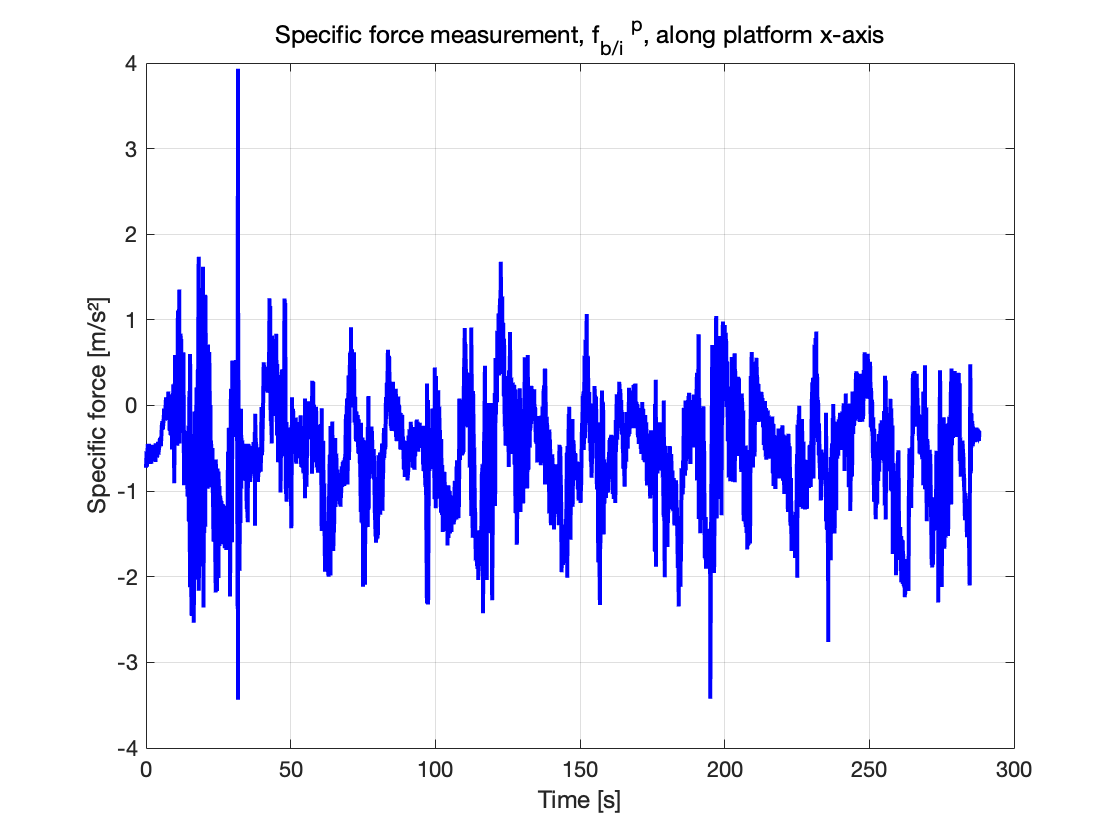
图 2：沿平台 x 轴的比力测量值

在比力测量值波形图中，我们观察到:

  • 比力（加速度）的幅值变化反映了车辆在行驶过程中不断加速（正）和减速（负）的状态，比力的变化有一定的周期性，周期的重复和饶建筑物的轨迹相关，每一圈的加速度变化特性相似。

  • 同时，比力测量中有较高的噪声波动，这是由于加速度计测量的随机噪声 n_f(t) 导致的。

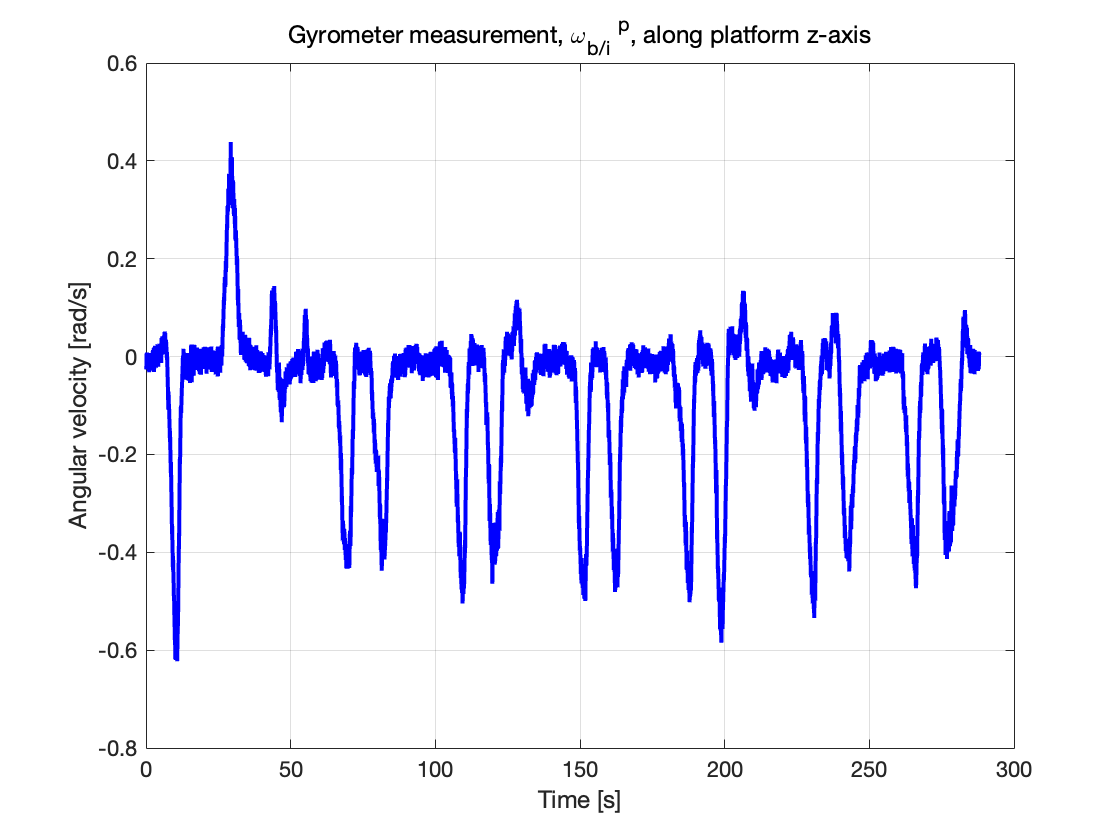
图 3：沿平台z 轴的角速度测量值

在角速度测量值波形图中，我们观察到:

  • 角速度正值表示车辆在逆时针方向（左）转弯，负值表示车辆在顺时针方向（右）转弯，因此我们可见，角速度的波形变化完全符合车辆运动轨迹，从原点出发，向右行驶产生一个负的角速度峰值，再向左转弯产生一个正的角速度峰值，随后不断右转，一直产生周期性的负峰值，共计12次，符合绕三圈每次右转4次的真实情况。在角速度接近于0的部分，车辆几乎直线行驶。

  • 我们还可以看出 陀螺仪测量数据中存在一定的随机噪声n^\omega(t)（白噪声）。

坐标轴对应关系的推导

接下来我们推导坐标轴之间的对应关系，平台坐标系p 相对于车辆坐标系b 只需要绕p 坐标系的x 轴旋转180°即可。因此，我们有：

R_{p2b} = R_x(180)

根据上述内容，参考系p 和b 的坐标轴之间的关系如下：

x^b = x^p
y^b = -y^p
z^b = -z^p

因此，旋转矩阵R_{p2b} 就有了

R_{p2b} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix}

然后我们给出 平台测量值和车辆测量值之间的关系:

特定力的关系：

\vec{f}_{IMU}^b = R_{p2b} \cdot \vec{f}_{IMU}^p

角速度的关系：

\vec{\omega}_{IMU}^b = R_{p2b} \cdot \vec{\omega}_{IMU}^p

接下来我们要计算一些运动方程，为了简化我们首先做出一些假设:

  • 忽略地球自转 \omega_{e/i} \approx 0

  • 重力在整个过程中不变

因此我们计算如下运动方程:

车辆沿轨迹方向速度v_{AT}^b(t)

测量的特定力\vec{f}_{b/t}^b(x)(t) 和加速度之间的关系为：

a_{b/t}^b(x)(t) = f_{b/t}^b(x)(t) - g \sin(\theta)

其中， \theta 为车辆的俯仰角。假设道路倾斜角可以忽略，即\theta = 0，则简化为：

a_{b/t}^b(x)(t) = f_{b/t}^b(x)(t)

对时间积分得到速度：

v_{AT}^b(t) = \int_0^t a_{b/t}^b(x)(\tau) \, d\tau = \int_0^t f_{b/t}^b(x)(\tau) \, d\tau

局部切平面下的北向位置 p_N^t(t)

北向位置取决于速度和航向角\psi(t)。在 LTP 参考系中，北向速度为：

v_N^t(t) = v_{AT}^b(t) \cdot \cos(\psi(t))

将该速度对时间积分，可以得到北向位置：

p_N^t(t) = \int_0^t v_N^t(\tau) \, d\tau = \int_0^t \left[v_{AT}^b(\tau) \cdot \cos(\psi(\tau))\right] \, d\tau

局部切平面下的东向位置p_E^t(t)

同样，东向位置也取决于速度和航向角\psi(t)。在 LTP 参考系中，东向速度为：

v_E^t(t) = v_{AT}^b(t) \cdot \sin(\psi(t))

将该速度对时间积分，可以得到东向位置：

p_E^t(t) = \int_0^t v_E^t(\tau) \, d\tau = \int_0^t \left[v_{AT}^b(\tau) \cdot \sin(\psi(\tau))\right] \, d\tau

航向角\psi(t) （基于欧拉角微分而来）

航向角由绕z 轴的角速度通过陀螺仪测得：

\dot{\psi}(t) = \omega_{b/i}^b(z)(t)

将该量对时间积分，可以得到航向角：

\psi(t) = \int_0^t \omega_{b/i}^b(z)(\tau) \, d\tau

在 LTP 下实现简化的 IRS 机理

在 2D 简化的 IRS 机理中，使用梯形积分法可以对航向角、纵向速度、北向和东向位置进行解算。

航向角 \hat{\psi}_{IRS}(k)

陀螺仪在b-坐标系下的测量量为

\omega_{IMU}^b(z)(k) \quad \text{and} \quad \omega_{IMU}^b(z)(k-1)

在连续时间中，航向角的微分满足

\dot{\psi}(t) \;=\; \omega_{b/i}^b(z)(t)

令离散时刻t_k = k \Delta t，采用梯形积分法近似得到：

\hat{\psi}_{IRS}(k) = \hat{\psi}_{IRS}(k-1) + \frac{\Delta t}{2} \bigl[ \tilde{\omega}_{IMU}^b(z)(k-1) + \tilde{\omega}_{IMU}^b(z)(k) \bigr]

  • \hat{\psi}_{IRS}(k-1) 为上一时刻k-1 的航向角估计值


纵向速度\hat{v}_{AT_{IRS}}^b(k)

加速度计在b-坐标系下的测量为

f_{IMU}^b(x)(k)\quad\text{and}\quad f_{IMU}^b(x)(k-1)

假设道路倾斜可忽略，车辆俯仰角较小，沿车辆前向（$x^b$ 轴）的线加速度可直接由加速度计输出得到。令上一时刻k-1 的纵向速度估计为\hat{v}_{AT_{IRS}}^b(k-1)，则同样使用梯形积分法：

\hat{v}_{AT_{IRS}}^b(k) = \hat{v}_{AT_{IRS}}^b(k-1) + \frac{\Delta t}{2} \bigl[ \tilde{f}_{IMU}^b(x)(k-1) + \tilde{f}_{IMU}^b(x)(k) \bigr]

北向位置p_{n_{IRS}}^t(k)

设上一时刻北向位置估计为\hat{p}_{n,IRS}^t(k-1)，仍使用梯形积分对速度积分可得：

\hat{p}_{n,IRS}^t(k) \;=\; \hat{p}_{n,IRS}^t(k-1) \;+\; \frac{\Delta t}{2}\Bigl[v_{n,IRS}^t(k) \;+\; v_{n,IRS}^t(k-1)\Bigr]

我们将北向速度带入：

v_{n,IRS}^t(k) \;=\; \hat{v}_{AT,IRS}^b(k-1)\,\cos\bigl(\psi_{IRS}(k)\bigr)

因此得到

\hat{p}_{n,IRS}^t(k) \;=\; \hat{p}_{n,IRS}^t(k-1) \;+\; \frac{\Delta t}{2} \Bigl[ \hat{v}_{AT,IRS}^b(k-1)\,\cos\bigl(\hat{\psi}_{IRS}(k-1)\bigr) \;+\; \hat{v}_{AT,IRS}^b(k)\,\cos\bigl(\hat{\psi}_{IRS}(k)\bigr) \Bigr]

东向位置p_{e_{IRS}}^t(k)

同理可得上一时刻的东向位置为p_{e_{IRS}}^t(k-1)，则

\hat{p}_{e,IRS}^t(k) \;=\; \hat{p}_{e,IRS}^t(k-1) \;+\; \frac{\Delta t}{2}\Bigl[v_{e_{IRS}}^t(k) \;+\; v_{e_{IRS}}^t(k-1)\Bigr]

我们将东向速度公式带入:

v_{e_{IRS}}^t(k) \;=\; \hat{v}_{AT_{IRS}}^b(k)\,\sin\bigl(\psi_{IRS}(k)\bigr)

因此得到

\hat{p}_{e,IRS}^t(k) \;=\; \hat{p}_{e,IRS}^t(k-1) \;+\; \frac{\Delta t}{2} \Bigl[ \hat{v}_{AT,IRS}^b(k-1)\,\sin\bigl(\hat{\psi}_{IRS}(k-1)\bigr) \;+\; \hat{v}_{AT,IRS}^b(k)\,\sin\bigl(\hat{\psi}_{IRS}(k)\bigr) \Bigr]

运行代码得到相关结果如下

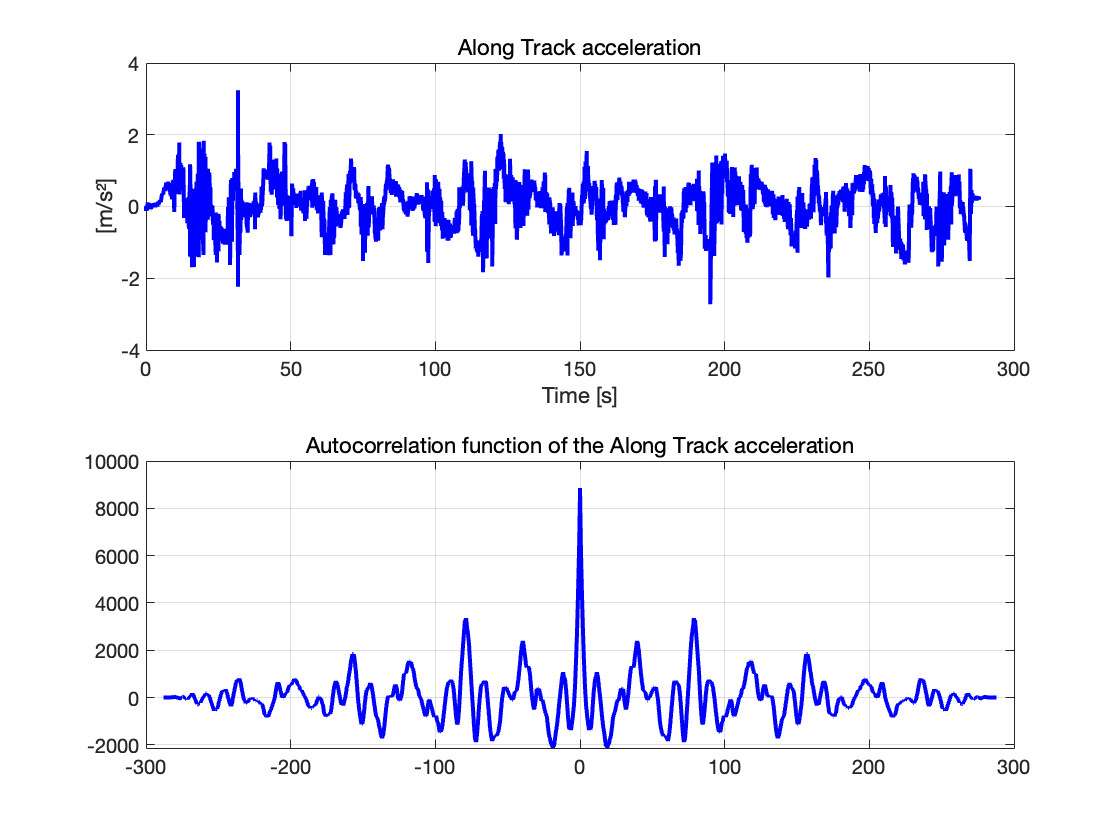
图 4：沿着轨迹方向 加速度波形及自相关函数

上面的图展示了加速度沿轨迹方向（车辆前进方向x^b 轴）测量的比力大小。我们可见加速度依旧围绕0波动，正值表示加速，负值表示减速，并且有一定的周期性规律。同时，数据中包含测量噪声。

下图展示了加速度沿轨迹方向的自相关函数，可见:

  • 自相关函数在 t=0 处得到最大值，表明加速度与自身完全相关，符合自相关函数的定义。

  • 自相关函数在t=0 处左右对称，表明加速度信号的相关性与时间延迟方向无关。

  • 尽管自相关函数在中心峰值之后快速衰减，但自相关函数值并不为0，因此可以看出车辆在短时间内的运动行为具有惯性，即当前加速度值收到上一时刻动态行为的印象。

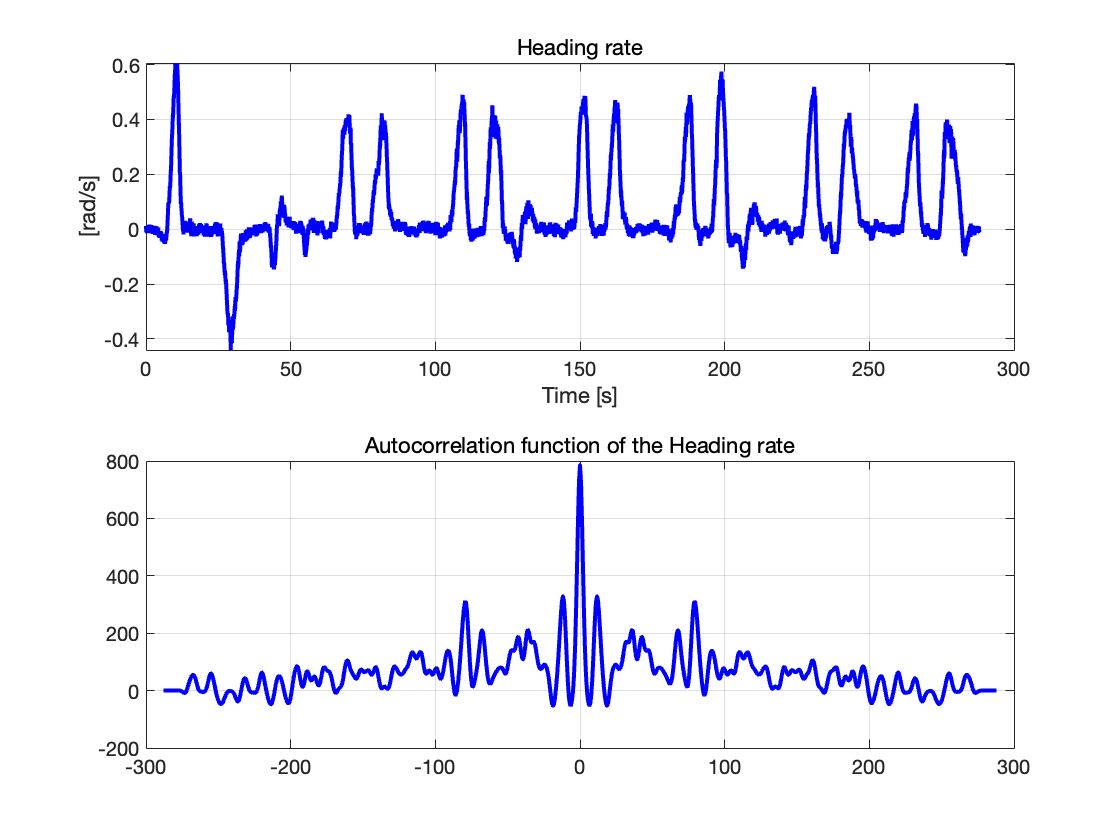
图 5：航向角速率及其自相关函数

上图是航向角速度波形，和我们之前分析相同，不过正负号相反，汽车在先右转再左转后开始绕建筑物旋转三圈，使得这部分的航向角速度波形图呈现周期性，并转弯12次，符合3圈的路径。

下图是航向角速率的自相关函数，我们可以看出:

  • 在中心\tau = 0（无延迟）处，自相关函数最大，表示航向角速率与自身完全相关。

  • 自相关函数在t=0 处左右对称，表明的航向角速率相关性与时间延迟方向无关。

  • 自相关函数在峰值附近快速下降，但并不为0，反映航向角速率的短时间相关性较强，而长时间相关性较弱，体现出了航向角速度的惯性

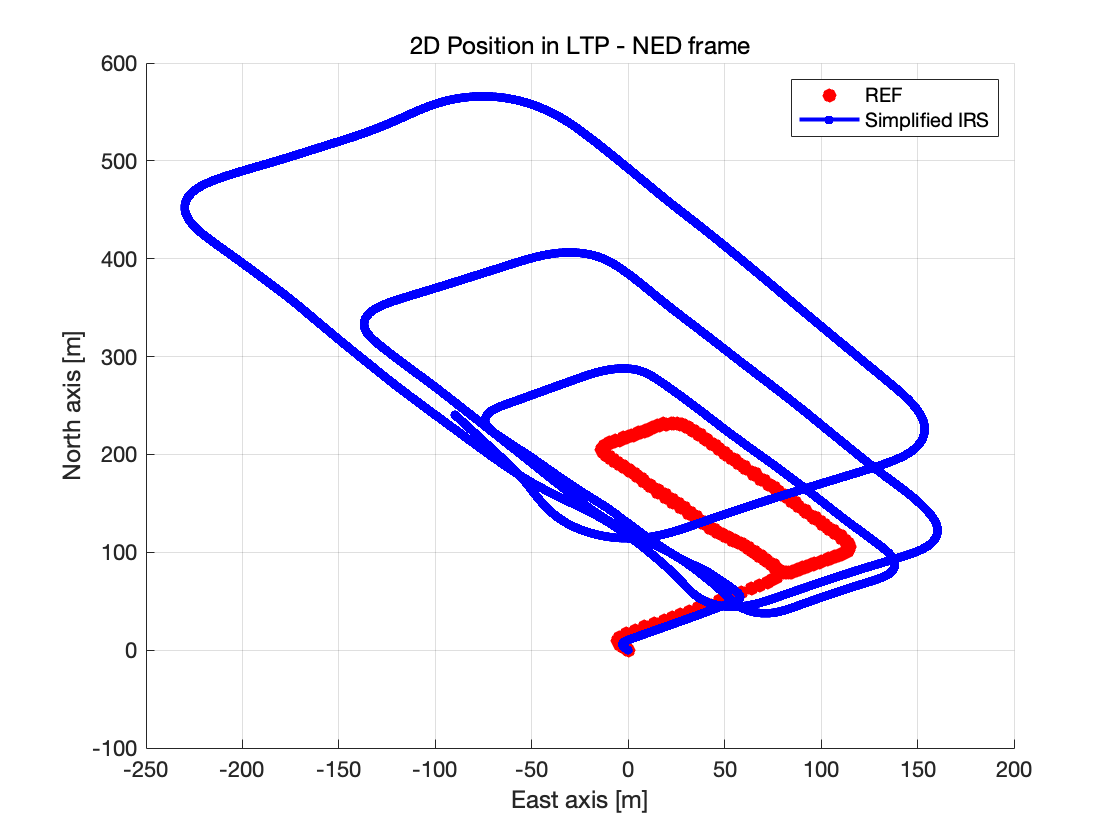
图 6：简化 IRS 轨迹与参考轨迹对比

红色线参考轨迹，蓝色线是经过简化惯性导航系统（IRS）计算出的车辆轨迹，利用低成本 IMU 的输出数据（加速度计和陀螺仪），基于推算得到的位置估计。我们可以从中观察到:

  • 估计轨迹和参考轨迹的总体轨迹形状是一致的，说明简化后的IRS捕捉到了车辆运动的动态特性

  • 估计轨迹随着时间逐渐偏离参考轨迹，尤其在第二圈和第三圈后，轨迹出现了严重的漂移（尤其北向和东向），这种漂移是由于惯性导航系统的累积误差（偏置和噪声）导致的。

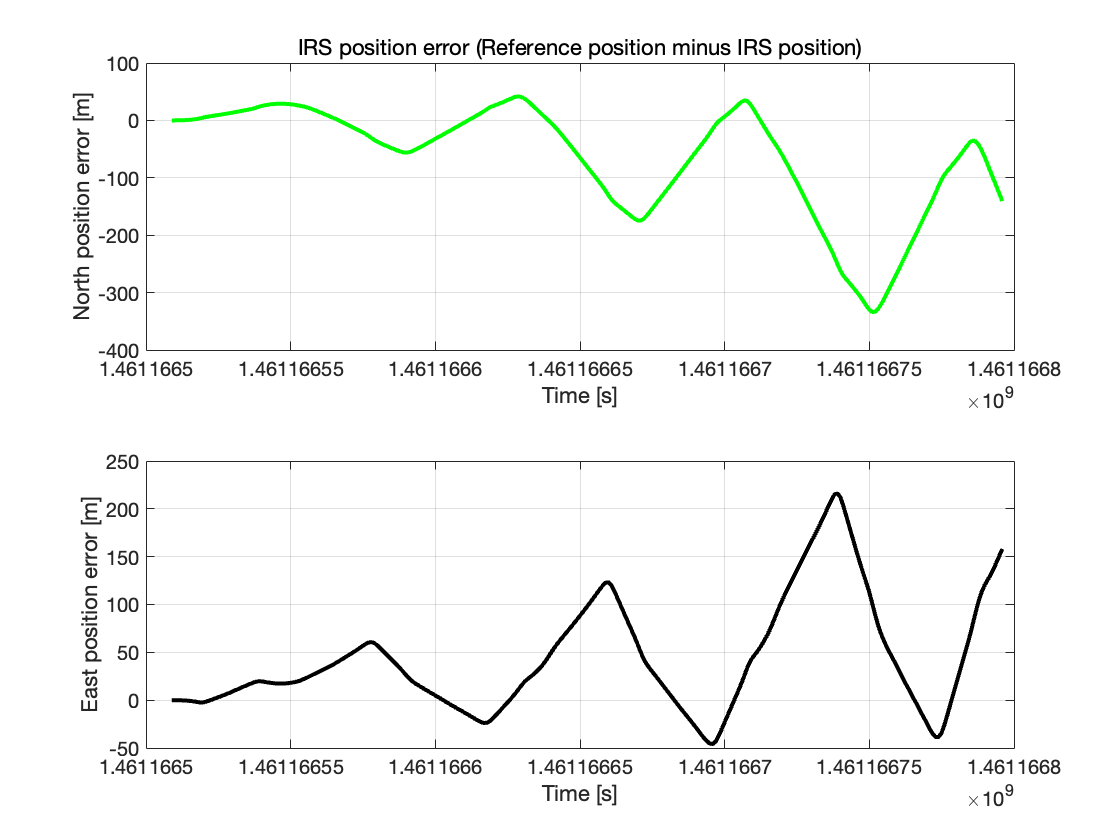
图 7：简化 IRS 的北向与东向位置误差

上图代表了北向的误差，可见:

  • 随时间推进，误差幅值逐渐增大，表现为误差的累积效应。

  • 误差呈现出明显的周期性波动，与车辆沿路径绕行的周期一致。

上图代表了东向的误差，可见:

  • 同样，随时间推进，误差幅值逐渐增大，累积效应明显。

  • 同样，表现出明显的周期性波动，与车辆路径的周期一致。

简化 IRS 通过对陀螺仪和加速度计数据进行积分来推算位置，导致测量误差（偏置和噪声）随着时间累积。并且，简化 IRS 系统没有外部校正信息（如 GPS 数据），因此误差会随着时间推移而累积放大。

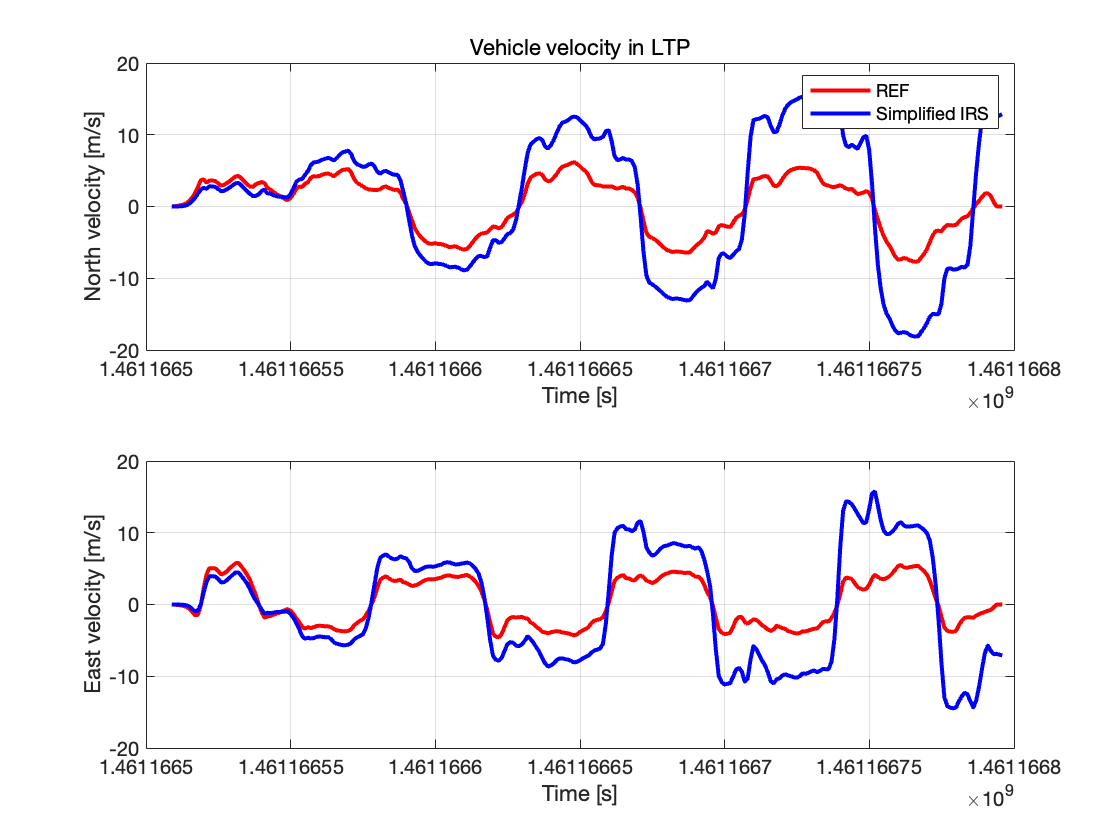
图 8：车辆在局部切平面中的北向和东向速度

上图代表了车辆的北向速度，并比较了估计值和参考值，我们可见，简化IRS得到的估计值捕捉到了北向速度的变化趋势，但随着时间推移，误差越来越大。

下图代表了车辆的东向速度，我们可以得到相同的结论，估计值捕捉到了东向速度的变化趋势，但随着时间推移误差增大。与之前的结果分析相符合。

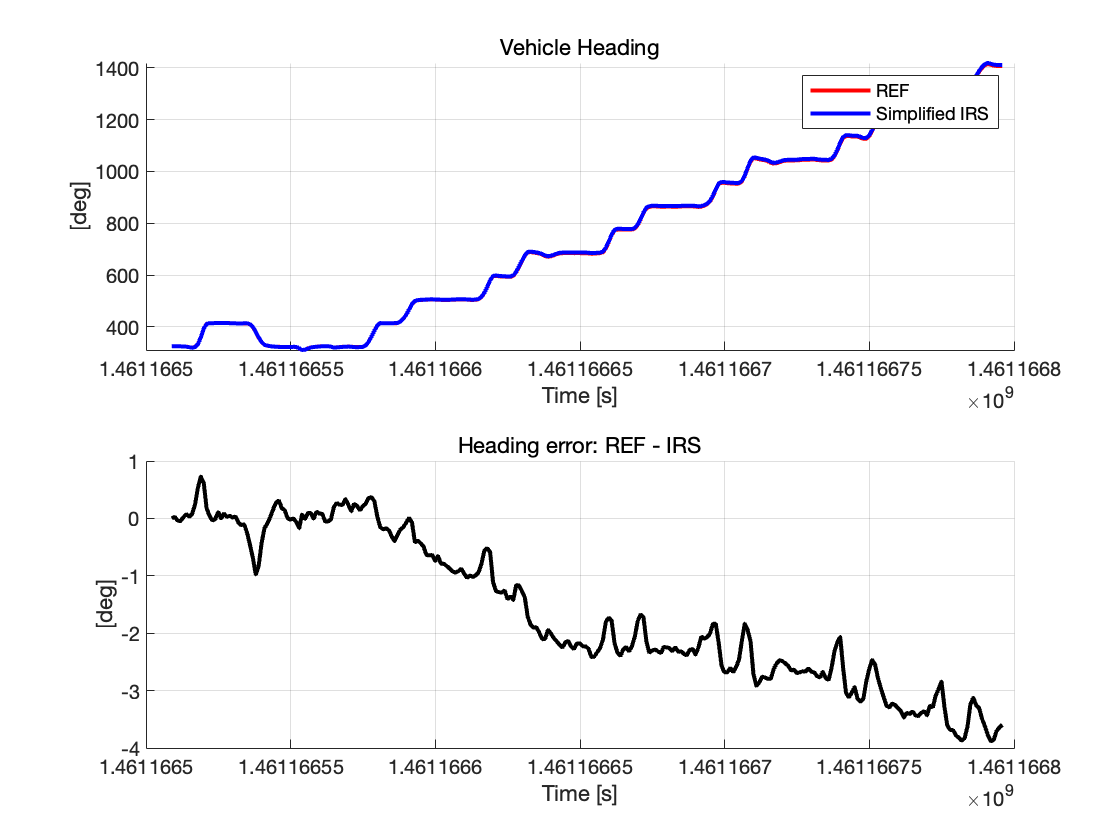
图 9：车辆航向角及误差

上图是车辆航向角的估计值和参考值比较，我们可以看出简化IRS得到的估计值和参考值波形几乎一致，可见简化IRS系统能够有效的跟踪车辆的航向角变化。

下图是更精细的观察航向角误差，我们看到误差范围从+1 到-4，并不算很大，但是可以看到随着时间推移，误差也有增大的趋势，说明航向角误差也在随着时间而积累，这种漂移的主要来源是陀螺仪的偏置误差。

从上述所有结果来看，简化后的IRS系统误差随着时间不断积累，且无外部校正，漂移无法被抑制，因此后面我们要使用线性化卡尔曼滤波来融合GPS 和 IRS 数据，来校正误差

地面车辆的 GPS/IRS 松耦合

松耦合是把 GPS 和 IRS（惯性参考系统）的数据“合起来用”的一种方法。IRS 本身会随着时间积累误差，而 GPS 数据能提供比较准的位置，但有时候信号会丢失（比如在隧道里）。通过结合两者的数据，我们可以修正 IRS 的误差，得到更可靠的导航解。

这里我们用的工具是 线性化卡尔曼滤波器，它专门用来结合不同来源的数据，估计某个系统的状态。简单来说，它负责 监听 GPS 和 IRS 的数据，然后判断哪个更靠谱，最终得出一个“综合解”。

卡尔曼滤波器的状态转移模型定义如下：

\delta \dot{x}(t) \;=\; F(t)\,\delta x(t) + u(t)
y(t) \;=\; H(t)\,\delta x(t) + w(t)

其中：

  • \delta x(t) 是误差状态向量

  • ​​F(t) 是状态转移矩阵

  • y(t) 是观测量向量

  • H(t) 是观测矩阵

  • u(t) 是过程噪声

  • w(t) 是观测噪声

误差状态向量为：

\delta x(t) = \begin{bmatrix} \delta p_n(t) & \delta p_e(t) & \delta v_{AT}^b(t) & b^f(t) & \delta \psi(t) & b^\omega(t) \end{bmatrix}^\top

其中变量含义如下:

变量

内容

\delta p_n(t)

IRS 在 t-坐标系下的北向位置误差

\delta p_e(t)

IRS 在 t-坐标系下的东向位置误差

\delta v_{AT}^b(t)

IRS 在 b-坐标系下表征的沿轨迹方向速度误差

b^f(t)

IMU 加速度计偏置（误差来源于加速度计的不准确）

\delta \psi(t)

IRS 的航向角误差（IRS 导航解中航向角与真实值的偏差）

b^\omega(t)

IMU 陀螺仪偏置（误差来源于陀螺仪的不准确）

\delta s = s - \hat{s}_{IRS}

对任意误差量的定义：真实值 s 与 IRS 解算值 \hat{s}_{IRS} 的差值

北向位置误差

位置的北向分量定义如下：

\dot{p}_n^t(t) = v_{AT}^b (t) \cdot \cos \psi (t)

北向位置误差定义为：

\delta \dot{p}_n(t) =\dot{p}_n^t (t) - \dot{p}_{n,IRS}^t (t)

将 \dot{p}_n^t(t) 代入后，有：

\delta \dot{p}_n (t) = g(v_{AT}^b (t), \psi (t)) - g(\hat{v}_{AT,IRS}^b (t), \hat{\psi}_{IRS}(t))

其中：

g(v_{AT}^b (t), \psi (t)) = v_{AT}^b (t) \cdot \cos \psi (t)

对 g(v_{AT}^b(t), \psi(t)) = v_{AT}^b(t) \cos(\psi(t)) 进行泰勒级数展开，在 IRS 解附近线性化：，可得：

g(v_{AT}^b (t), \psi (t)) \approx g(\hat{v}_{AT,IRS}^b (t), \hat{\psi}_{IRS}(t)) + \left. \frac{\partial g}{\partial v_{AT}^b} \right|_{v_{AT}^b = \hat{v}_{AT,IRS}^b} \cdot \delta v_{AT}^b (t) + \left. \frac{\partial g}{\partial \psi} \right|_{\psi = \hat{\psi}_{IRS}} \cdot \delta \psi (t)

计算偏导数：

\frac{\partial g}{\partial v_{AT}^b (t)} = \cos \psi (t) \quad \quad\frac{\partial g}{\partial \psi} = - v_{AT}^b (t) \cdot \sin \psi (t)

代入 \delta p_n (t) 的方程，得：

\delta \dot{p}_n (t) = \cos \hat{\psi}_{IRS} (t) \cdot \delta v_{AT}^b (t) - \sin \hat{\psi}_{IRS} (t) \cdot \hat{v}_{AT,IRS}^b (t) \cdot \delta \psi (t)

这样，我们就计算出了卡尔曼滤波器中北向位置的状态转移模型，该模型通过围绕 IRS 解进行一阶展开，涵盖了与速度和方向相关的误差。

东向位置误差

东向位置分量定义为：

\dot{p}_e^t (t) = v_{AT}^b (t) \cdot \sin \psi (t)

类似于北向位置误差，定义 g(v_{AT}^b (t), \psi (t)) = v_{AT}^b (t) \cdot \sin \psi (t) ，计算偏导数：

\frac{\partial g}{\partial v_{AT}^b (t)} = \sin \psi (t) \quad \quad \frac{\partial g}{\partial \psi} = v_{AT}^b (t) \cdot \cos \psi (t)

代入 \delta p_e (t) 的方程，得：

\delta \dot{p}_e (t) = \sin \hat{\psi}_{IRS} (t) \cdot \delta v_{AT}^b (t) + \cos \hat{\psi}_{IRS} (t) \cdot \hat{v}_{AT,IRS}^b (t) \cdot \delta \psi (t)

沿跑道方向的速度误差

使用这些测量数据，我们在 b 坐标系中定义沿跑道方向的速度误差：

\dot{v}_{AT}^b (t) = f_{IMU}^b (x) (t) = \vec{f}_{IMU}^b (x) (t) + b_x^f (t)

误差定义为：

\delta \dot{v}_{AT}^b (t) = \dot{v}_{AT}^b (t) - \hat{\dot{v}}_{AT,IRS}^b (t)

根据 IMU 模型，我们得到沿跑道方向速度误差的动态方程：

\delta \dot{v}_{AT}^b (t) = \delta b_x^f (t)

  • 其中 \delta b_x^f (t) 为加速度计在 x 轴上的偏差误差。

加速度计偏差误差

加速度计偏差误差定义为：

\delta b_x^f (t) = b_x^f (t) - \hat{b}_x^f (t)

对该表达式求导，得到：

\delta \dot{b}_x^f (t) = \dot{b}_x^f (t) - \hat{\dot{b}}_x^f (t)

根据 IMU 模型，我们得出加速度计偏差误差的动态方程：

\delta \dot{b}_x^f (t) = - \frac{1}{\tau_f} \delta b_x^f (t) + n_f^b (t)

因此我们使用 IMU 传感器测量加速度，同时 b^f (t) 偏差遵循一阶马尔可夫过程，其建模如下：

\begin{cases} \vec{f}^b (t) = f^b (t) - b^f (t) - n^f (t) \\ \dot{b}^f (t) = - \frac{1}{\tau_f} b^f (t) + n_f^b (t) \end{cases}

 

航向角误差

航向角 \psi (t) 的演变遵循以下动态方程：

\dot{\psi} (t) = b^\omega (t)

误差定义为：

\delta \psi (t) = \psi (t) - \hat{\psi} (t)

对该表达式求导，得到：

\delta \dot{\psi} (t) = \dot{\psi} (t) - \hat{\dot{\psi}} (t)

代入 IMU 模型中 \dot{\psi} (t) 的表达式，得：

\delta \dot{\psi} (t) = - \delta b^\omega (t)

陀螺仪偏差误差

陀螺仪偏差误差定义为：

\delta b_x^\omega (t) = b_x^\omega (t) - \hat{b}_x^\omega (t)

对该表达式求导，得到：

\delta \dot{b}_x^\omega (t) = \dot{b}_x^\omega (t) - \hat{\dot{b}}_x^\omega (t)

根据 IMU 模型，我们得出陀螺仪偏差误差的动态方程：

\delta \dot{b}_x^\omega (t) = - \frac{1}{\tau_\omega} \delta b_x^\omega (t) + n^{b^\omega}(t)

状态转移矩阵

在卡尔曼滤波框架下，状态转移方程为：

\delta \dot{x} (t) = F(t) \delta x (t) + u(t)

状态转移矩阵 F(t) 为：

F(t) = \begin{bmatrix} 0 & 0 & \cos (\hat{\psi} (t)) & 0 & -\hat{v}_{AT,IRS}^b (t) \sin (\hat{\psi} (t)) & 0 \\ 0 & 0 & \sin (\hat{\psi} (t)) & 0 & \hat{v}_{AT,IRS}^b (t) \cos (\hat{\psi} (t)) & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -\frac{1}{\tau_f} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & -\frac{1}{\tau_\omega} \end{bmatrix}

过程噪声

基于前述计算，我们可以定义过程噪声向量如下：

u(t) = \begin{bmatrix} \sigma_p^n & \sigma_p^e & \sigma_v & n^{b^f} (t) & \sigma_\psi & n^{b^\omega} (t) \end{bmatrix}^T

协方差矩阵

假设过程噪声的所有分量在时间上是独立且不相关的，我们可以确定协方差矩阵 Q_t ：

Q = \text{diag} \left( (\sigma_p^n)^2, (\sigma_p^e)^2, (\sigma_v)^2, (\sigma_b^f)^2, (\sigma_\psi)^2, (\sigma_b^\omega)^2 \right)

  • 其中， n^{b^f}(t) \sim N(0, \sigma_{b^f}^2) 是加速度计偏差噪声， n^{b^\omega}(t) \sim N(0, \sigma_{b^\omega}^2) 是陀螺仪偏差噪声。

因此， Q 是一个对角矩阵，其对角元素对应于加速度计和陀螺仪偏差噪声的方差。

对时间模型进行离散化

1. 状态转移模型

在连续时间中，系统状态的演化由以下状态方程描述：

\delta \dot{x}(t) = F(t) \cdot \delta x(t) + u(t)

为了对该模型进行离散化，我们假设时间被划分为小的间隔 \Delta t ，并且在某个时刻的状态可以通过前一时刻的状态以及状态转移模型进行预测。离散化后的状态方程为：

\delta x[k+1] = F_k \cdot \delta x[k] + u_k

状态转移矩阵 F(t) 在连续时间下可通过线性近似进行离散化。常见的方法是使用欧拉近似，此时矩阵 F_k 计算如下：

F_k = I + \Delta t \cdot F_t + \frac{\Delta t^2}{2} \cdot F_t^2

  • 这个公式对矩阵 F(t) 在时间间隔 \Delta t 内进行线性近似。

2. 过程噪声协方差

过程噪声 u(t) 由协方差矩阵 Q_t 在连续时间下建模，同时也需要离散化。离散化的过程噪声协方差矩阵 Q_k 计算如下：

Q_k = Q_t \cdot \Delta t + \frac{\Delta t^2}{2} \cdot (F_t Q_t + Q_t F_t^T)

  • 这一表达式描述了过程噪声协方差在离散时间步长 \Delta t 内的演化。

3. 卡尔曼滤波更新

在每个时间步，使用离散时间模型传播状态和协方差：

X_{\text{pred}} = F_k \cdot X_{\text{prev}}, \quad S_{\text{pred}} = F_k \cdot S_{\text{prev}} \cdot F_k^T + Q_k

GPS 测量数据以 1/F_s 秒的间隔间歇性地集成（其中 F_s 为 GPS 采样频率）。然后计算卡尔曼增益 ( K )，并更新预测状态和协方差。

计算卡尔曼滤波测量模型

定义 GPS 测量

观测模型将误差向量与 GPS 位置测量联系起来：

y(k) = H(t) \delta x(k) + w(k)

在这里，我们不直接使用 GPS 位置测量值（LTP 坐标系中的北/东坐标），而是使用测量向量：

y(k) = \begin{bmatrix} \tilde{p}_{n,GPS}^t (k) \\ \tilde{p}_{e,GPS}^t (k) \end{bmatrix}

在误差空间中，该测量值对应于位置误差 \delta p_n^t (k) 和 \delta p_e^t (k) ：

\tilde{p}_{n,GPS}^{t}(k) = p_n^t(k) + n_{p_n,GPS}(k)
\tilde{p}_{e,GPS}^{t}(k) = p_e^t(k) + n_{p_e,GPS}(k)

将 GPS 测量与位置误差关联

IRS 提供位置误差 \delta p_n^t (k) 和 \delta p_e^t (k) 和位置估计 \hat{p}_{n,IRS}^{t} (k) 和 \hat{p}_{e,IRS}^{t} (k) 的相关公式如下:

\delta p_n^t (k) = p_n^t (k) - \hat{p}_{n,IRS}^{t} (k)
\delta p_e^t (k) = p_e^t (k) - \hat{p}_{e,IRS}^{t} (k)

GPS 测量与 IRS 估计值之间的差异导致创新项：

\tilde{p}_{n,GPS}^{t} (k) - \hat{p}_{n,IRS}^{t} (k) \simeq \delta p_n^t (k) + n_{p_n,GPS}(k)
\tilde{p}_{e,GPS}^{t} (k) - \hat{p}_{e,IRS}^{t} (k) \simeq \delta p_e^t (k) + n_{p_e,GPS}(k)

用向量形式表示：

y(k) = \begin{bmatrix} y_n (k) \\ y_e (k) \end{bmatrix} = \begin{bmatrix} \delta p_n^t (k) \\ \delta p_e^t (k) \end{bmatrix} + \begin{bmatrix} n_{p_n,GPS} (k) \\ n_{p_e,GPS} (k) \end{bmatrix}

测量矩阵 H(k)

我们打算写成之前的矩阵形式:

y(k) = H \cdot \delta x(k) + w(k)

之前假设的状态误差向量为：

\delta x(k) = \begin{bmatrix} \delta p_n (t) \\ \delta p_e (t) \\ \delta v_{AT}^b (t) \\ b^f (t) \\ \delta \psi (t) \\ b^\omega (t) \end{bmatrix}^T

误差向量的前两个分量 \delta p_n^t (k) 和 \delta p_e^t (k) 正是 GPS 测量得到的误差值。其他分量（如 \delta v_{AT}^b (k) 、 b^f (k) 、 \delta \psi (k) 、 b^\omega (k) ）不会直接出现在 GPS 位置观测中。因此，测量矩阵 H(k) 为：

GPS 测量直接与北向和东向位置误差 \delta p_n^t (k) 和 \delta p_e^t (k) 相关，但不直接受其他状态变量（如速度、航向、偏差）影响。因此，测量矩阵 H(k) 可表示为：

H(k) = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{bmatrix}

该矩阵用于从状态向量 \delta x(k) 中提取北向和东向位置误差进行测量。

测量噪声 w(k)

测量噪声向量定义如下，同时假设它们是相互独立的高斯随机变量：

w(k) = \begin{bmatrix} n_{p_n,GPS} (k) \\ n_{p_e,GPS} (k) \end{bmatrix}

  • 其中， \sigma_{p_n,GPS} = \sigma_{p_e,GPS} = 10m 。

测量噪声协方差矩阵 R(k)

由于 n_{p_n\text{,GPS}}(k) 和 n_{p_e\text{,GPS}}(k) 是独立同分布的，我们可以将测量噪声协方差矩阵 R(k) 建模为对角矩阵，其中对角元素分别是 \sigma_{p_n\text{,GPS}}^2 和 \sigma_{p_e\text{,GPS}}^2 ：

R(k) = \mathbb{E} [w(k) \cdot w^T (k)] = \begin{bmatrix} \sigma_{p_n,GPS}^2 & 0 \\ 0 & \sigma_{p_e,GPS}^2 \end{bmatrix}

已知 \sigma_{p_n,GPS}^2 = \sigma_{p_e,GPS}^2 = 10^2 ，所以最终的测量噪声协方差矩阵为：

R(k) = \begin{bmatrix} 10^2 & 0 \\ 0 & 10^2 \end{bmatrix}= \begin{bmatrix} 100 & 0 \\ 0 & 100 \end{bmatrix}

该矩阵表明：

  • 北向和东向测量噪声之间不相关（非对角元素为零）。

  • 每个方向的测量噪声方差为 100，对应标准差 10 米。

  • 这反映了 GPS 位置测量误差的统计特性，并在卡尔曼滤波更新步骤中用于计算权重。

实现

卡尔曼滤波流程

时间传播（状态预测）

卡尔曼滤波器的第一步是根据前一时刻 k-1 的状态预测当前时刻 k 的状态。系统状态由状态向量 X_k 表示（包含位置、速度等），它通过离散化的状态转移矩阵 F_k 在时间上进行传播。同时，该步骤还需要预测状态协方差矩阵 S_k ，表示对状态估计的不确定性。

预测的状态计算如下：

X_{\hat{k}} = F_k \cdot X_{\hat{k-1}}

  • X_{\hat{k}} 是预测的状态，

  • X_{\hat{k-1}} 是上一时刻的状态估计。

x_hat = Fk * X_hat;  % X_hat = X_k|k-1

预测的协方差计算如下：

S = F_k \cdot S \cdot F_k^T + Q_k

  • S 是预测的状态协方差矩阵，

  • Q_k 是过程噪声的协方差矩阵。

S = Fk * S * Fk' + Qk;  % S = cov(X_k|k-1)

测量更新（修正）

卡尔曼滤波的第二步是利用在时刻 k 获得的测量值更新状态估计。滤波器使用测量值 y_k （在本例中是 GPS 位置或速度），并通过测量矩阵 H 将状态向量 X_k 与测量值关联：

y_k = H \cdot X_k + w_k

计算卡尔曼增益 卡尔曼增益 K_k 用于衡量测量值相对于预测值的重要性。计算方法如下：

V = H \cdot S \cdot H^T + R
K = S \cdot H^T \cdot V^{-1}

  • V 是创新协方差，衡量测量误差的影响，

  • K 是卡尔曼增益，用于调整状态估计。

V = H * S * H' + R;  % Innovation covariance
K = S * H' * inv(V); % Kalman gain

更新状态估计 然后，使用创新项（测量值与预测值之差）来更新状态：

X_{\hat{k}} = X_{\hat{k}} + K \cdot \text{innov}

  • 创新项 \text{innov} = y_k - H \cdot X_{\hat{k}} 代表测量值和预测值的差异。

x_hat = x_hat + K * innov;  % State estimate correction

更新协方差 最终，状态协方差 S_k 也需要更新，以反映新的不确定性：

S = S - K \cdot H \cdot S 
S = S - K * H * S;  % Covariance correction

GPS/IRS 融合与更新

第三步是融合惯性导航系统（IRS）和 GPS 的结果。卡尔曼滤波器结合这两个系统的估计结果，以获得更精确的状态估计。这通过将 IRS 的位置和速度估计与 GPS 观测数据融合来实现。

状态向量更新如下：

p_{n,GPS\_IRS}(i) = p_{n,ins}(i) + X_{\hat{k}}(1)
p_{e,GPS\_IRS}(i) = p_{e,ins}(i) + X_{\hat{k}}(2)
\psi_{i,GPS\_IRS}(i) = \psi_{i,ins}(i) + X_{\hat{k}}(5)

类似地，速度分量也按照相同方式更新。这些步骤在每个时间步都重复，以便随着新数据的到来不断更新状态估计。

处理 IRS 和 GPS 数据频率不同的问题

由于 IRS 和 GPS 采样频率不同，卡尔曼滤波器需要处理这个频率差异。在状态更新过程中，滤波器会根据 IRS 的数据频率进行状态传播，而 GPS 数据用于间歇性校正。

IRS 预测

由于 IRS数据（加速度计和陀螺仪测量值） 采样率较高，它用于连续估计车辆的状态（位置、速度、方向等）：

X_k = F_k \cdot X_{k-1} + u_k
S_k = F_k \cdot S_{k-1} \cdot F_k^T + Q_k

这一预测仅基于 IRS 数据，每个时间步 \Delta t 都会执行一次。

GPS 数据更新

GPS 数据（包括位置和速度估计）采样率较低，因此状态更新仅在 GPS 数据可用时进行。测量值 y_k 由 GPS 提供，并用于与 IRS 估计进行比较：

y_k = H \cdot X_k + w_k

当 GPS 数据可用时，计算卡尔曼增益：

K_k = S_k \cdot H^T \cdot (H \cdot S_k \cdot H^T + R_k)^{-1}

然后更新状态：

X_k = X_k + K_k \cdot (y_k - H \cdot X_k)

并更新协方差矩阵：

S_k = (I - K_k \cdot H) \cdot S_k

这样，卡尔曼滤波器利用 GPS 数据校正状态估计，并考虑测量误差和噪声。

GPS 信号屏蔽处理

在某些情况下，GPS 信号可能会暂时丢失。为了解决这个问题，卡尔曼滤波器可以继续使用 IRS 数据进行状态传播，而不会执行 GPS 相关的更新。GPS 信号屏蔽由一个掩码向量控制，该向量指示 GPS 数据是否可用：

MaskingInterval = Min_MaskingInterval : Min_MaskingInterval + MaskingInterval - 1;
Masking(i_{GPS}) = 1  % 当 GPS 信号丢失时

这保证了即使 GPS 数据间歇性丢失，卡尔曼滤波器仍然可以继续运行，并在 GPS 数据恢复后进行校正。

IRS 校正（GPS 更新时）

当 GPS 数据可用时，IRS 估计需要与 GPS 观测进行对比，以计算创新项 \nu_k ：

\nu_k = y_k - H \cdot X_k

然后计算卡尔曼增益：

K_k = S_k \cdot H^T \cdot (H \cdot S_k \cdot H^T + R_k)^{-1}

最终，利用卡尔曼增益调整状态估计：

X_k = X_k + K_k \cdot \nu_k

并更新协方差矩阵：

S_k = (I - K_k \cdot H) \cdot S_k

这样，滤波器能够在 GPS 数据可用时校正 IRS 估计，确保系统状态的高精度。

 

卡尔曼滤波器进行 GPS/IRS 融合

我们将分析使用卡尔曼滤波器进行 GPS/IRS 融合的性能，并模拟 GPS 信号丢失的情况。

情况一: GPS 数据持续可用，无中断

当以 MaskingInterval = 0s 运行 MATLAB时，卡尔曼滤波器会连续利用 GPS 数据来对 IRS 导航解决方案进行不间断校正。

轨迹比较

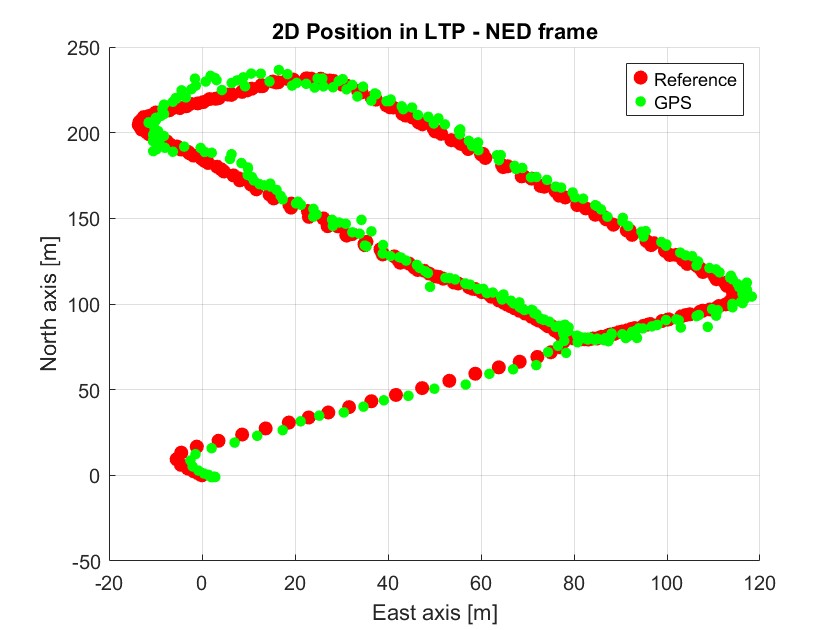
该图显示了车辆在局部切平面（LTP）坐标系中的 2D 位置：

  • 红色曲线：参考位置（理论、准确数据）

  • 绿色曲线：GPS 接收器测量得到的数据

可见GPS 轨迹紧随参考轨迹，表明 GPS 提供了相对精确的位置信息。但仍然存在一些偏差，这是因为 GPS 信号本身不精确（多路径效应）以及 GPS 系统本身的定位误差

GPS 位置/速度误差

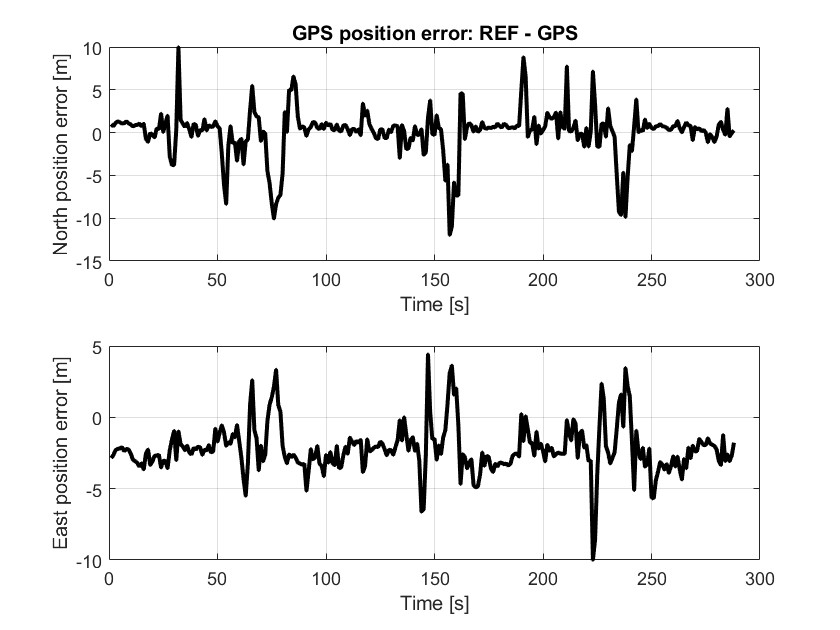
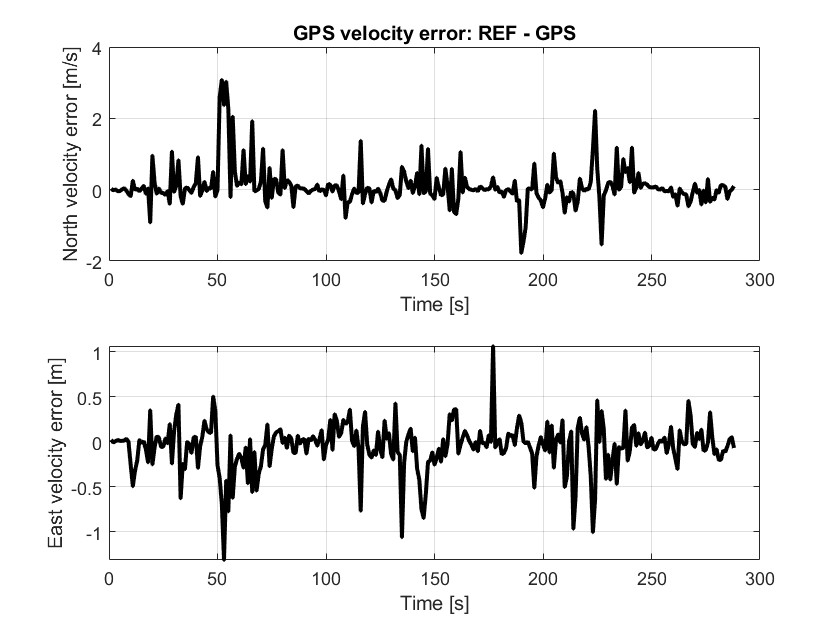
  • GPS 位置误差相对于参考位置有较大的波动，在某些时刻存在峰值，这是因为这个时间段GPS 信号受到干扰影响，测不准。

  • GPS 速度误差同样表现出波动，但总体误差较小，说明GPS 提供的速度估计相对更准确一些。

GPS/IRS 融合分析

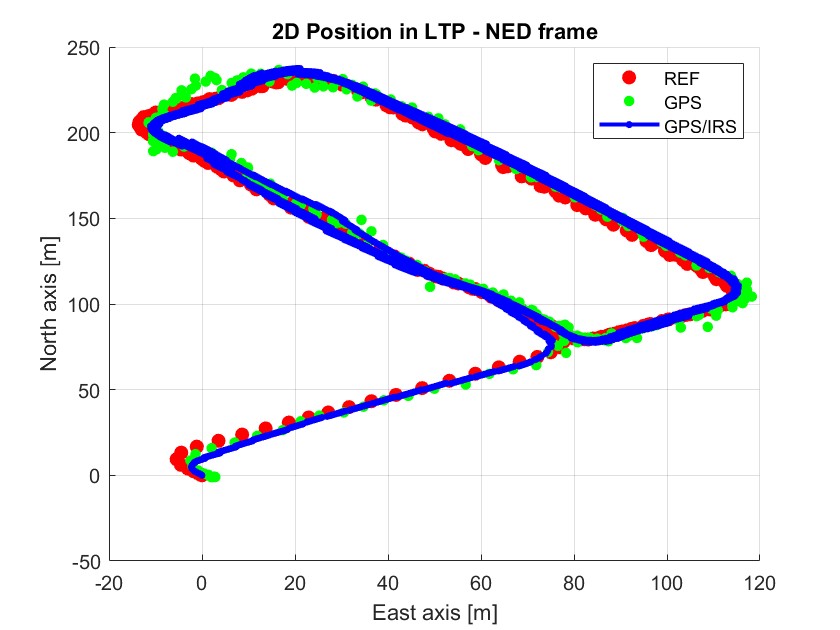
可见GPS/IRS 融合解结合提高了估计精度。

  • 绿色点：GPS 位置测量结果。

  • 蓝色曲线：GPS/IRS 融合解算的轨迹。

速度和航向角误差分析

IRS 误差分析（北、东向）

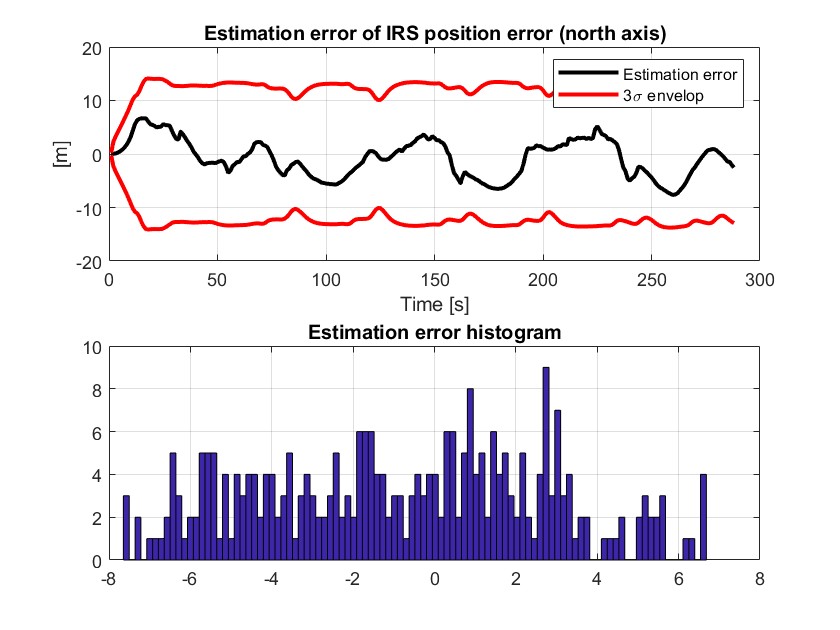
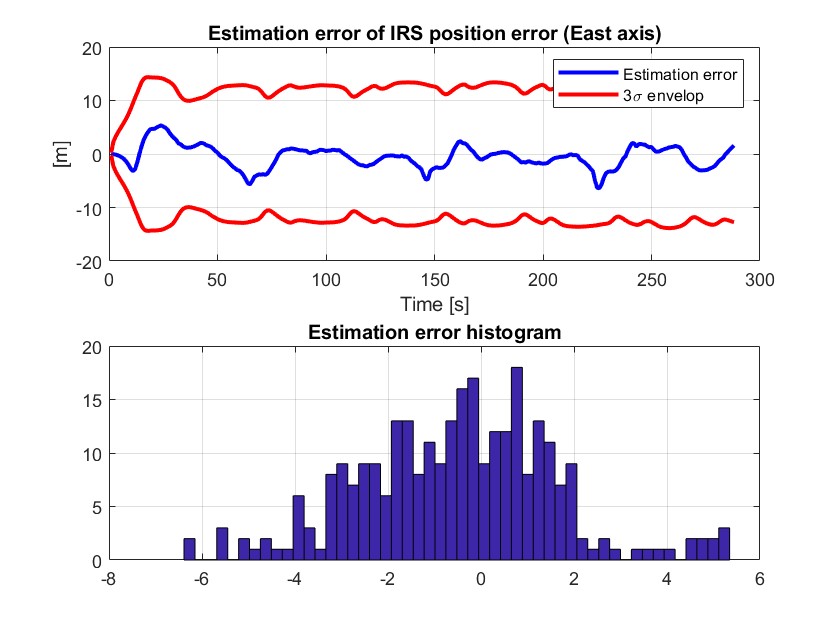
IRS 位置误差通常保持在三倍标准差范围内，误差直方图表明北向误差较为均匀，东向误差比较集中

北向误差的创新项及其直方图

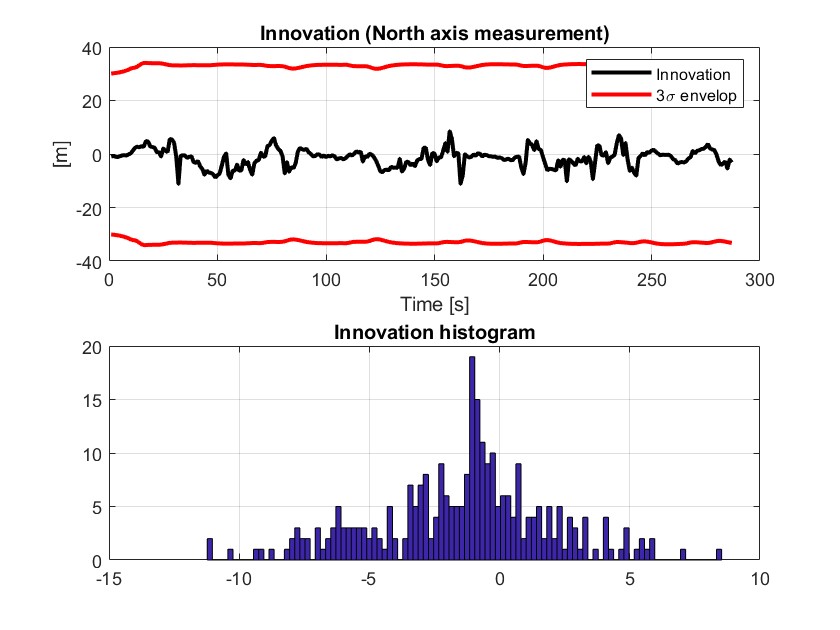
创新项振荡维持在零附近，非常的不错啊。

GPS/IRS 误差特性分析

仅依赖 IRS（加速度计和陀螺仪）会导致随时间累积误差（漂移），具体表现表现为位置和速度误差随时间增大，且长时间无修正。因此我们采用GPS/IRS 融合来让GPS 定期更新 IRS 估计，使得 IRS 误差不至于无限增长，同时融合解能够纠正漂移

滤波器更新频率的影响

卡尔曼滤波器通过每次更新调整 IRS 误差，使轨迹更加稳定和精确 ，IRS 适用于短期估计 ，但 GPS/IRS 结合可以保证长期导航精度。因此频繁的 IRS 更新 + GPS 低频校正 = 可靠的导航解算，即 IRS 负责高频平滑估计 ， GPS 负责低频校正漂移 ，这就是 最佳 GPS/IRS 更新策略

误差 锯齿 模式分析

GPS/IRS 误差曲线呈现 锯齿状变化 ，主要由于 IRS 误差随时间增长 ，直到 GPS 更新进行校正，产生一次大幅调整。因此误差的幅度依赖于 GPS 更新频率 ：

  • 更新频率高 → 锯齿效应减弱（平滑修正）。

  • 更新频率低 → 误差波动增大。

综上所述，GPS/IRS 结合能够显著提高导航精度，特别是在 GPS 信号间歇丢失的情况下，IRS 可提供短期的精确估计，而 GPS 校正确保长期精度。

情况二: GPS 数据每分钟被屏蔽，不可用

这段时间内，导航解完全依赖 IRS，直到 GPS 重新可用，卡尔曼滤波器才能进行校正。

GPS 失效期间的轨迹变化

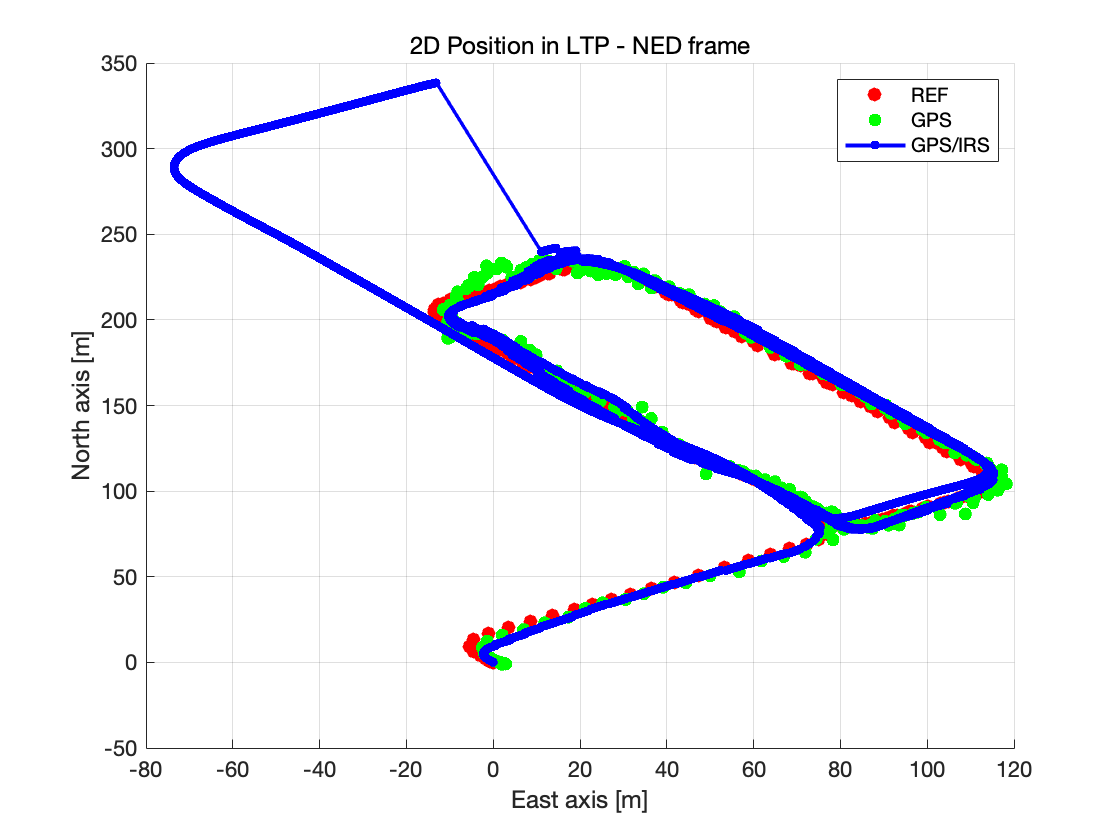
该图展示了 IRS 在 GPS 信号屏蔽期间的漂移程度，在 GPS 信号屏蔽期间，融合解算依赖于 IRS（惯性导航系统）进行导航。由于惯性导航的漂移累积，车辆轨迹逐渐偏离参考路径，当 GPS 数据重新可用时，卡尔曼滤波器会立即校正位置误差，从而导致车辆轨迹出现瞬时波动。

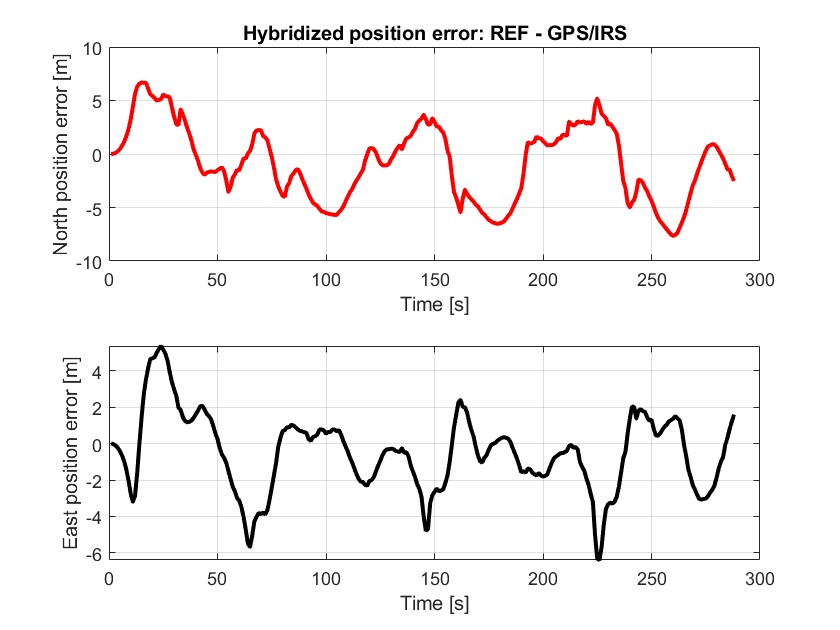
GPS/IRS混合位置误差

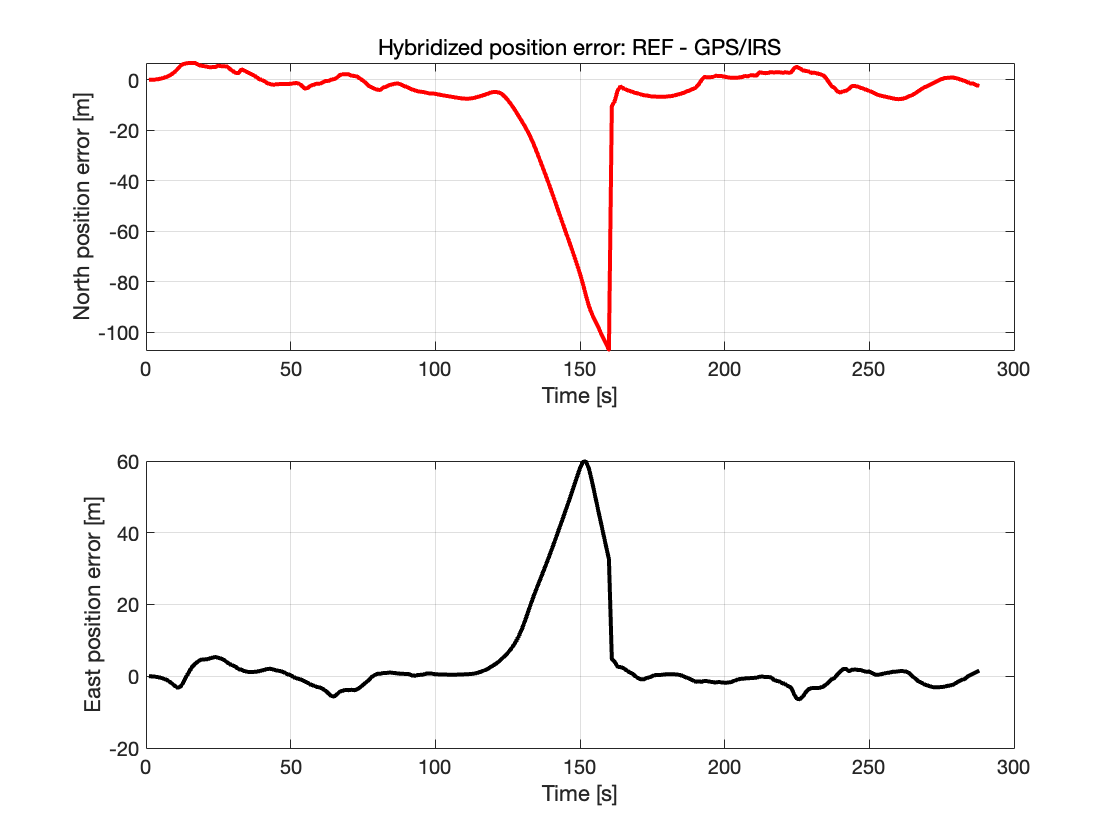
可以观察到北向和东向位置误差在长约60 秒的 GPS 屏蔽时间内不断累积，因为 IRS 的漂移误差无法实时校正。当屏蔽结束（即 GPS 数据重新可用）时，卡尔曼滤波器能够迅速修正误差，从而显著减少误差幅度。与 MaskingInterval = 0 时的误差曲线相比，可以看到屏蔽期间误差的波动更大

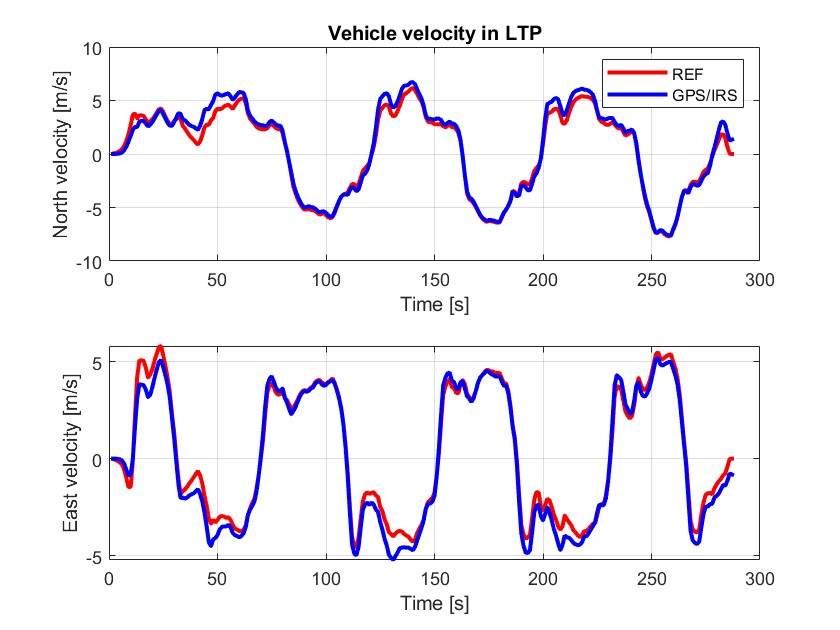
车辆在 LTP 坐标系下的速度

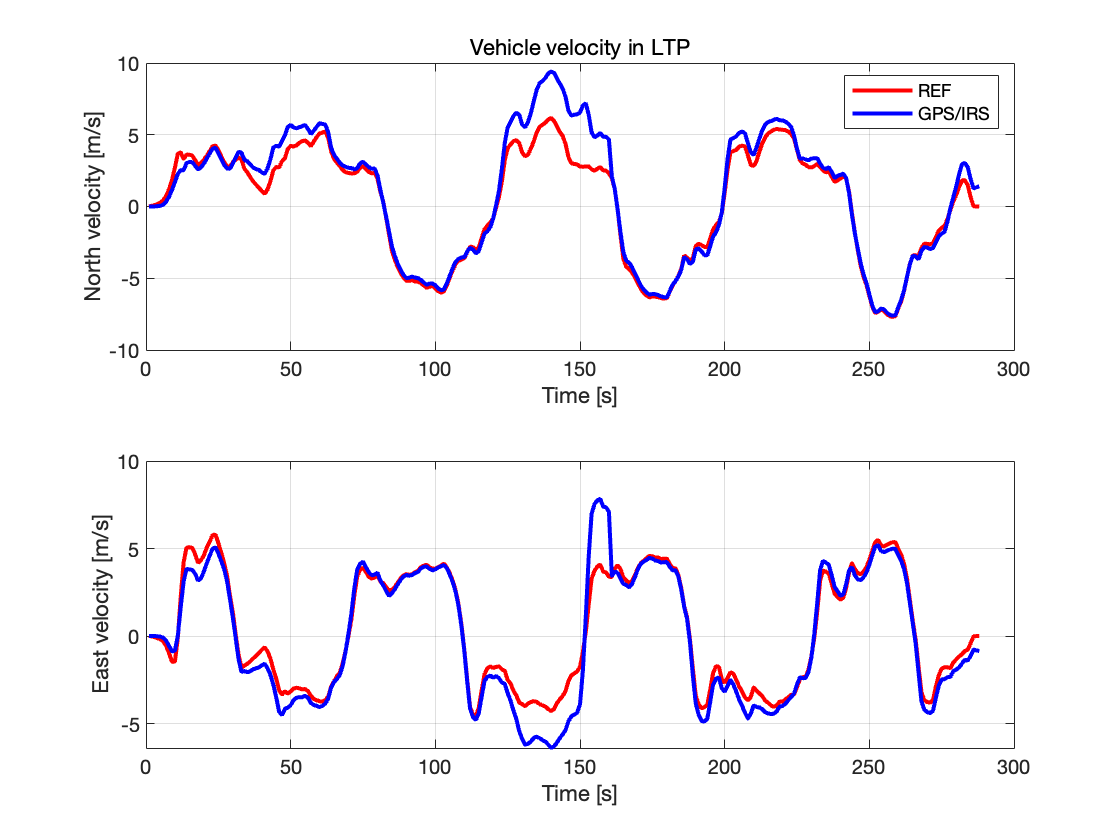
我们可以观察到，在 GPS 信号屏蔽期间（看对应的那段波形），IRS 仅依赖惯性导航进行速度估计，导致漂移的逐步累积，使速度估计与参考值出现偏差。当 GPS 数据恢复后，卡尔曼滤波器能够修正速度误差，使估计值迅速收敛至参考值。

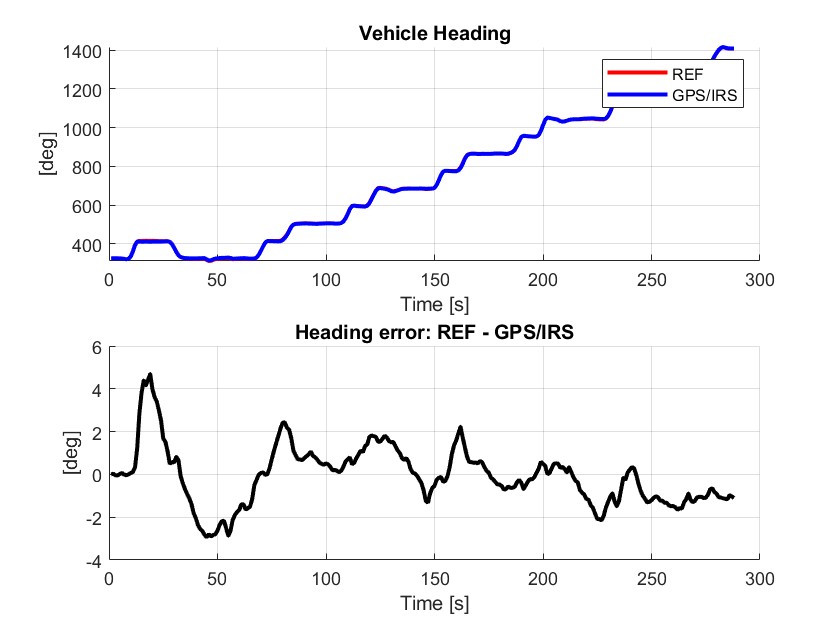
航向角及其误差

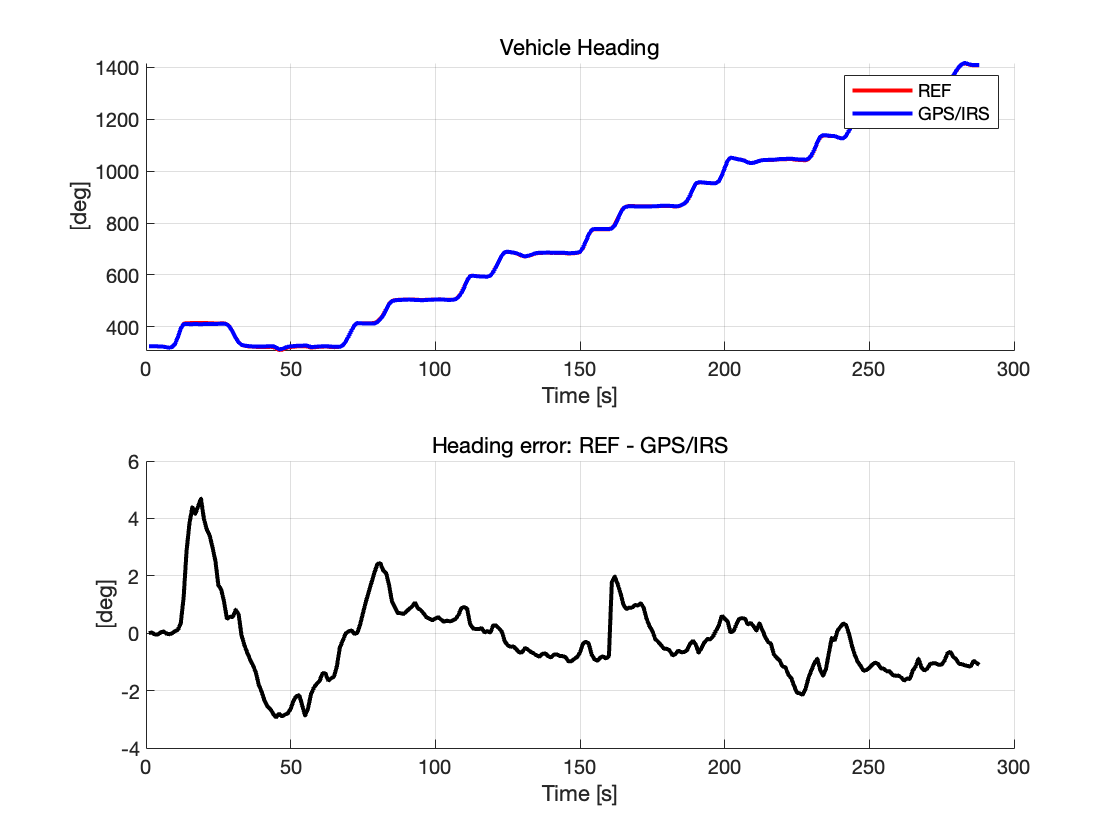
在 GPS 屏蔽期间，航向角误差也会逐步累积。屏蔽结束后，误差显著减小，说明 GPS 数据的恢复有效修正了 IRS 产生的航向角漂移。

IRS 位置误差估计（北向轴）

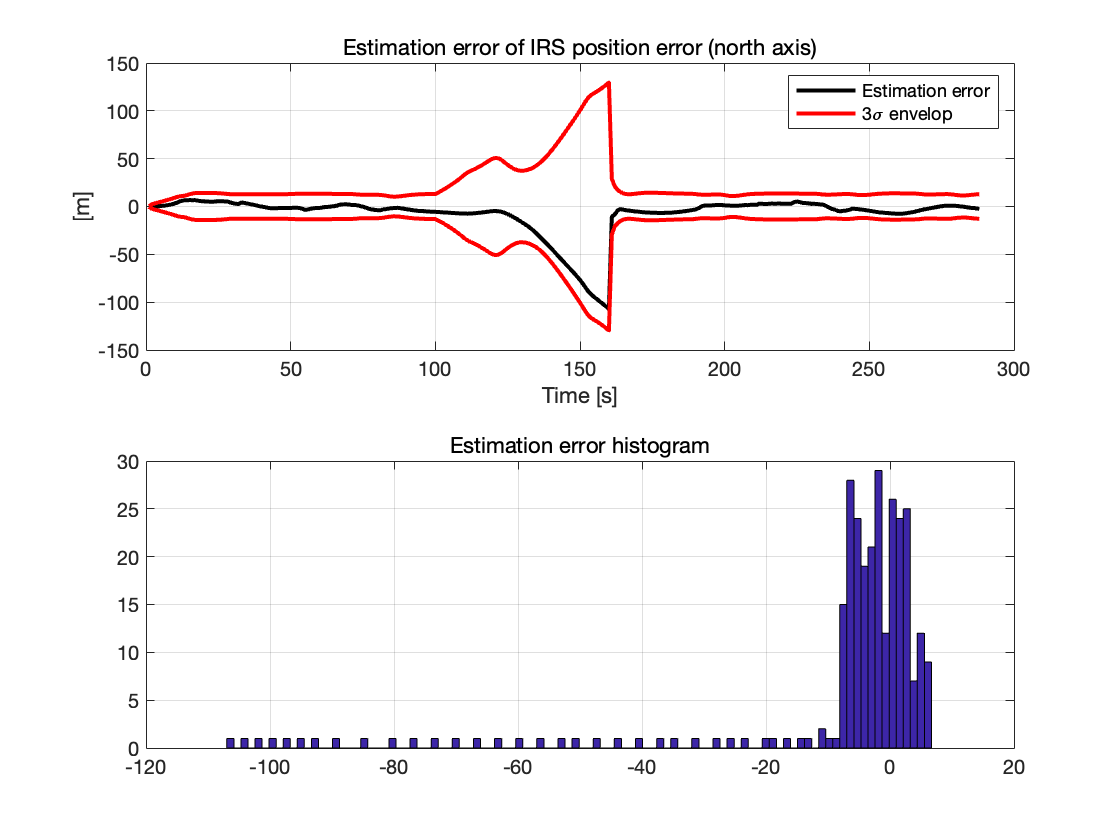
我们可以观察到，在 GPS 信号屏蔽期间，位置误差逐渐增加，但仍保持在 3σ 以内。这表明卡尔曼滤波器仍然能够有效估计误差。在屏蔽结束后，误差迅速减小并恢复至零，这说明 GPS 数据的重新引入成功修正了 IRS 的累积漂移。

IRS 位置误差估计（东向轴）

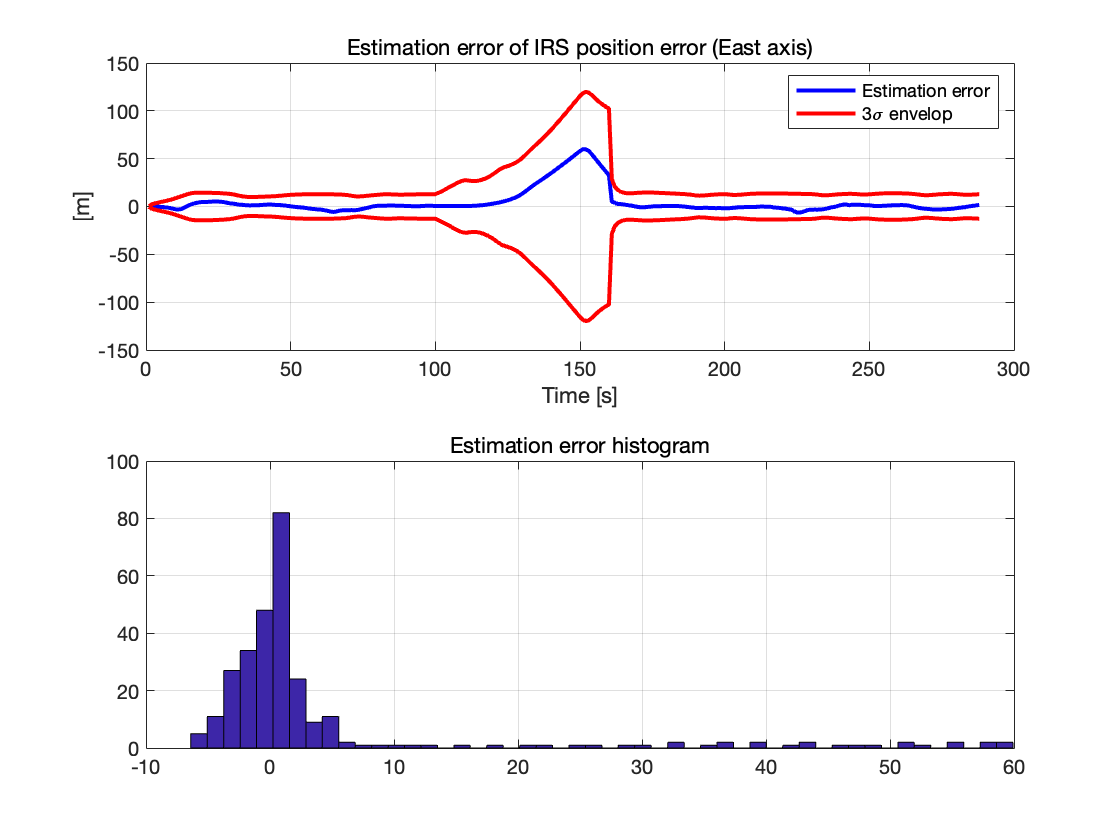
大多数误差值集中在零附近，系统整体误差总体较小，只有在 GPS 信号屏蔽期间，误差才会出现显著波动。

创新量（北向轴）

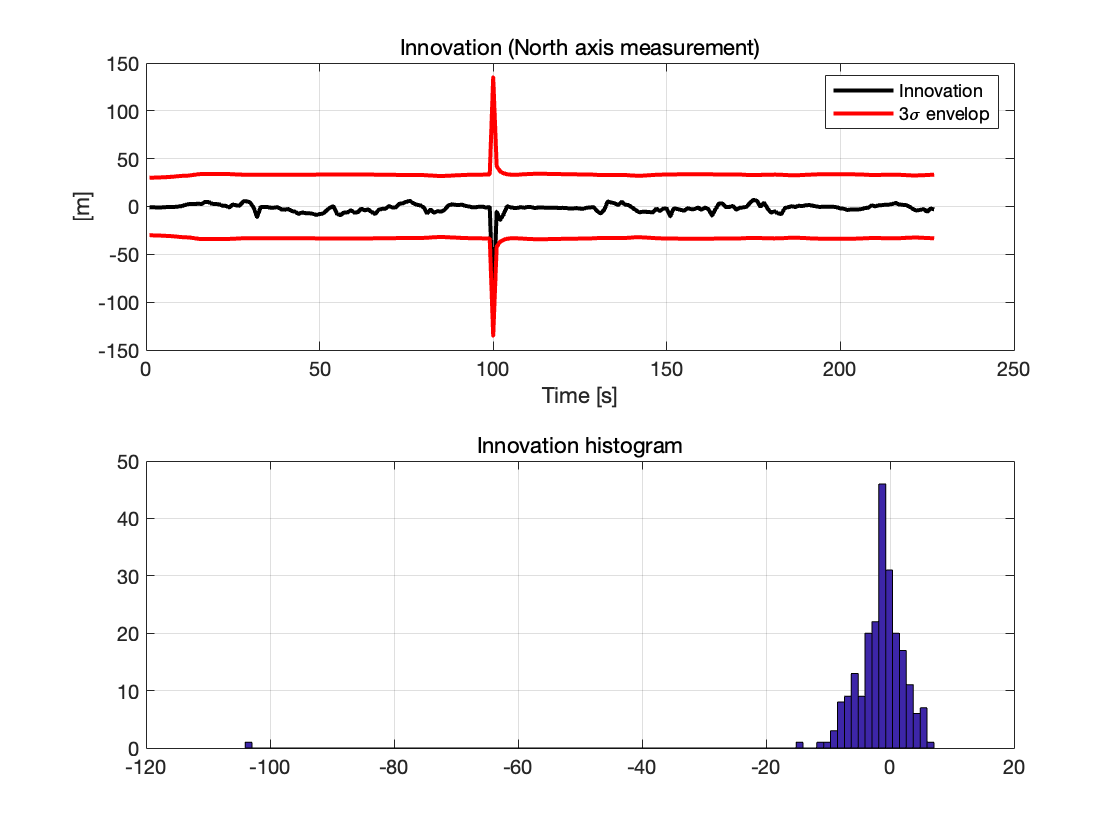
可以看到在 GPS 信号屏蔽结束时，创新量出现了一个明显的峰值，是因为 IRS 在屏蔽期间误差不断累积，导致测量值与预测值之间的偏差增大。当 GPS 数据恢复时，卡尔曼滤波器进行误差修正，使创新量迅速回归至零附近，可见系统在校正后恢复到稳定状态。

综上所述，GPS 数据的重新引入使得卡尔曼滤波器能够实时修正 IRS 产生的漂移误差。然而，在 GPS 信号屏蔽期间，IRS 独立计算导航解算，会导致误差逐渐累积，使轨迹逐渐偏离参考路径。当 GPS 数据恢复后，卡尔曼滤波器会立即修正这些累积误差，从而在导航轨迹上形成一个显著的误差峰值。

 

 

 

 

 

 

 

#GPS与导航 3
GPS与卫星导航：从非线性测量到精度因子评估
图像分割