GPS与卫星导航:从非线性测量到精度因子评估
编辑我们下面重点在于介绍如何基于卫星伪距测量来通过线性化最小二乘法求解GPS定位问题,首先我们进行ECEF(地心地固)与NED(北东地)双参考系转换,随后构建模型并进行梯度计算,最后利用几何精度稀释因子DOP来评估卫星几何结构对定位误差的影响,最后闲着没事验证一下算法的鲁棒性。
背景介绍
我们聚焦于一辆带有GPS的小车,绕着学校转圈,为了描述汽车的运动,我们要采用两个参考系:
参考系1(ECEF)
地球中心地固坐标系,原点位于地球中心O,x 轴指向黄道平面与格林尼治子午线的交点, z 轴与地球自转轴一致指向北极, y 轴则构成右手坐标系。一般GPS卫星坐标都用这个 表示
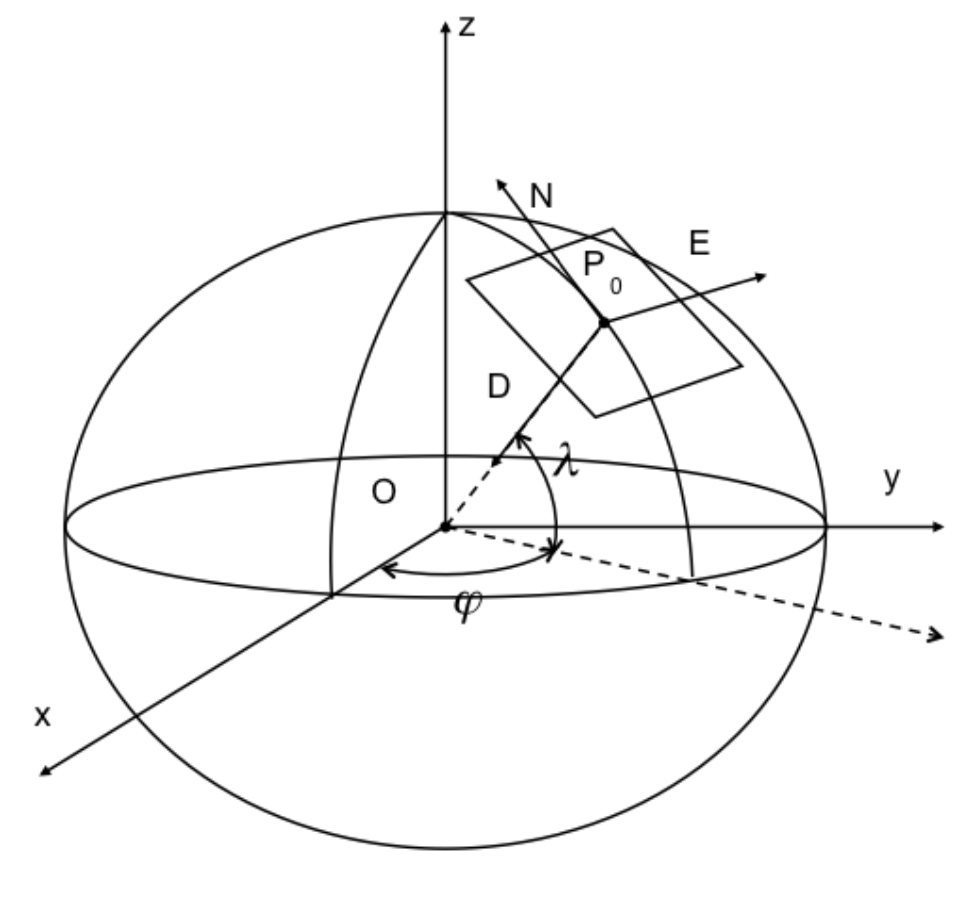
参考系2 (NED)
局部北东地坐标系,也就是我们平常用的上北下南坐标系,以地面上某个点P_0 为原点,其中各轴分别指向局部垂直、北和东。这个坐标系的意义在于直观展示车辆在局部地区的运动状态,比如说向南跑了200米。
两参考系之间的转换公式为
其中, X^1_0 = (x_0, y_0, z_0)^T 表示点P_0 在参考系1中的坐标,变换矩阵M 则由下式给出:
\lambda 和\phi 分别是参考点P_0 的经度和纬度。
车辆参考轨迹示意图如下:
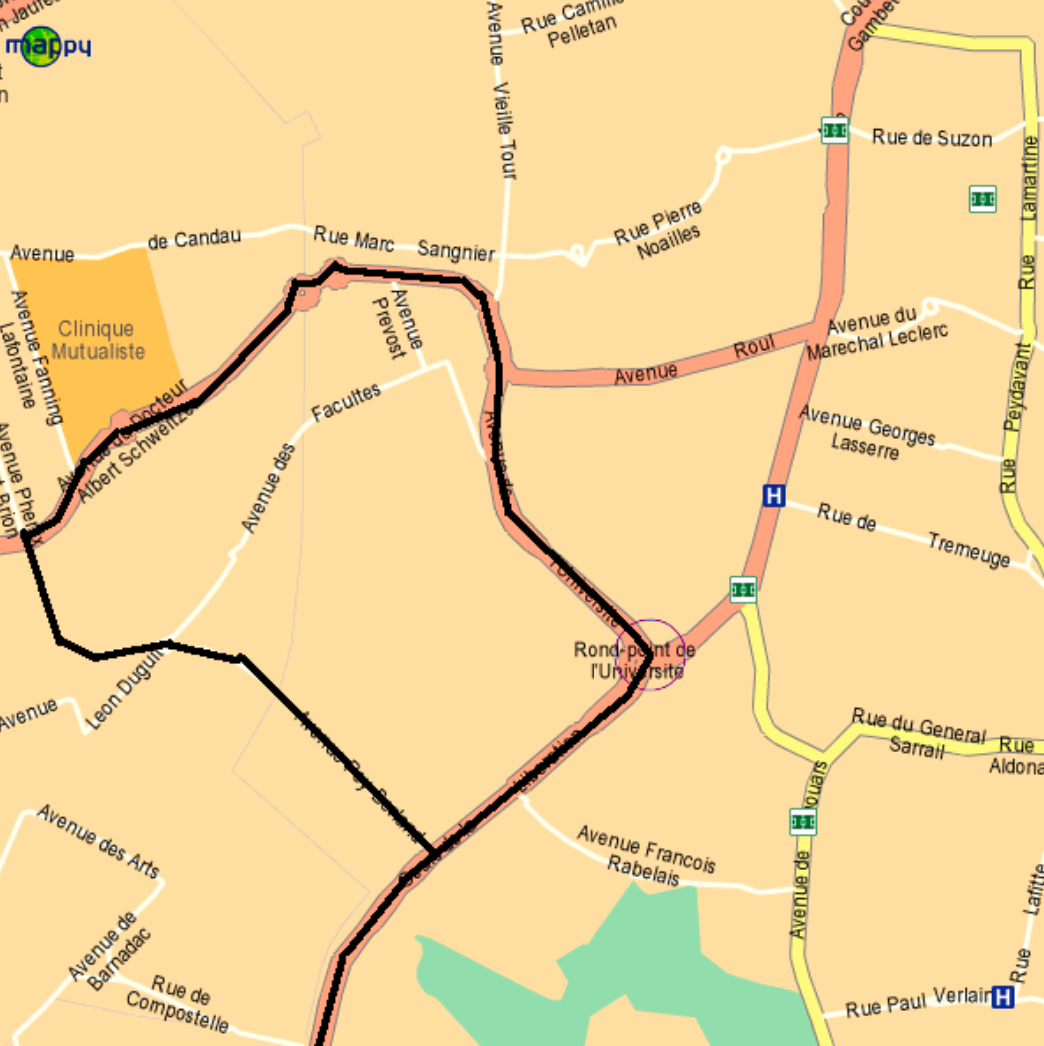
交代完了背景,我们要开始干活了,但是现在还不能急,我们要简单回顾一下最小二乘法。
利用最小二乘法计算位置
最小二乘法理论
最小二乘法用于从受噪声干扰的观测值中估计未知参数,假设观测模型为
其中:
X 是包含未知参数的状态向量
Z 是观测值向量
w 为观测噪声向量
最小二乘法的目标是找到估计值\hat{X} 使得二次误差 J(\xi) 最小
其闭式解为
(H^T H)^{-1} H^T 被称为伪逆矩阵
在GPS中的应用
在GPS定位问题中,状态向量X 包含车辆的三维位置(x, y, z) 以及接收器的时钟偏移b,即
GPS测量则是通过伪距来反映接收器与卫星之间的距离关系,数学模型表示为
其中
Y(t) = (Y_1, Y_2, \dots, Y_n)^T 表示时刻t 的n 个伪距测量
w(t) 是零均值、方差为\sigma^2 的高斯白噪声
函数h_t(x,y,z,b) 的具体形式如下
(x^i(t), y^i(t), z^i(t)) 是第i 颗卫星在时刻t 的坐标。
由于此模型是非线性的,为了使用最小二乘法,需要对公式进行线性化以便应用,在某一个参考点X_r 处对h_t 进行泰勒展开,可以得到线性化模型
H_t = \nabla h_t 表示h_t 对状态向量各分量的偏导数。
通过定义
即可将问题转化为标准线性模型,从而应用最小二乘法求解。选择的线性化参考点X_r 应尽量靠近真实状态向量 X ,以保证线性化误差较小。
在GPS导航中,通常选择前一个位置和时钟偏移的估计值作为线性化参考点。
H_t 矩阵的系数取决于GPS卫星相对于接收器的位置,该矩阵反映了卫星几何结构对位置估计误差的影响。
轨迹估计
首先我们补充一下关于坐标系旋转变换的知识,首先,假设点在参考系R'(轴为(x', y', z'))中的坐标为X',在参考系R(轴为(x, y, z))中的坐标为X,两者满足变换关系
矩阵M 的每一列表示R' 中单位向量在R 中的表示,当变换为绕z 轴旋转\theta 时, M 矩阵为:
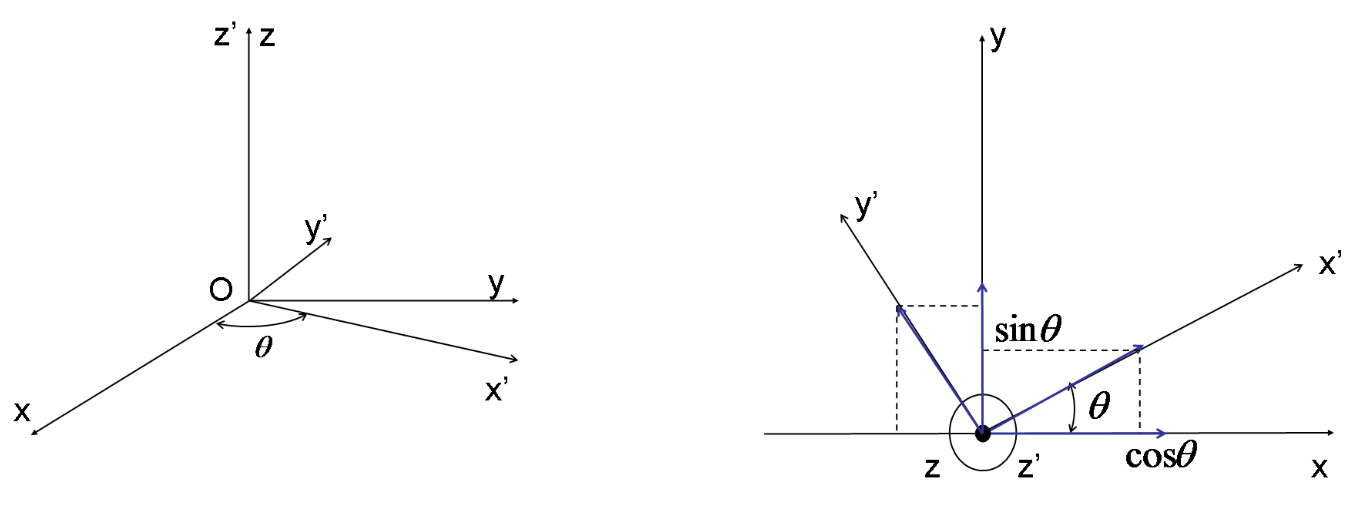
我们要经历两次旋转,将参考系1(地心地固 ECEF)转换到参考系2(本地 NED),并由此推导出 M 的表达式。
旋转1 – 绕Z 轴旋转
从 ECEF 坐标系开始,先绕Z 轴旋转角度\phi,变换矩阵为
旋转2 – 绕新Y 轴旋转
接着,将坐标系绕新Y 轴旋转角度-\left(\tfrac{\pi}{2}+\lambda\right),其变换矩阵为
最终变换 – 两次旋转矩阵的乘积
将两次旋转合并,变换矩阵 M 表达式为:
展开矩阵乘法后,结果为
下面我们通过程序llh2xyz 实现将参考点P_0 的椭球坐标转换到 ECEF 坐标。对于所研究的轨迹,参考点P_0 的大地坐标为:
纬度 \phi = 44^\circ48' \ \text{N}
经度 \lambda = 0^\circ35'\ \text{W} (注意西经为负)
高度 h = 0
转换步骤为:
将分分秒转换为小数度
转弧度
WGS84 椭球常数
利用如下代码进行计算:
% 定义经纬度和高度
latitude_deg = 44 + 48/60; % 纬度 44°48' 北
longitude_deg = -(0 + 35/60); % 经度 0°35' 西 (转换为负值)
altitude = 0; % 海拔高度,假设为 0 米
% 将经纬度从度转换为弧度
latitude_rad = deg2rad(latitude_deg); % 纬度转换为弧度
longitude_rad = deg2rad(longitude_deg); % 经度转换为弧度
% 创建包含纬度、经度和高度的向量
llh = [latitude_rad, longitude_rad, altitude];
% 调用 llh2xyz 函数计算 ECEF 坐标
xyz = llh2xyz(llh);
% 输出结果
disp('ECEF 坐标:');
disp(['X: ', num2str(xyz(1)), ' m']);
disp(['Y: ', num2str(xyz(2)), ' m']);
disp(['Z: ', num2str(xyz(3)), ' m']);得到结果 ECEF 坐标:
X: 4533051.770408139 m
Y: -46152.987854075 m
Z: 4471583.372126530 m我们再计算理论结果来进行验证,利用公式将大地坐标(\phi, \lambda, h) 转换为 ECEF 笛卡尔坐标 (X,Y,Z) 坐标:
其中 N(\phi) 表达式如下,我们可以根据之前信息计算其数值:
最终得到理论下的 ECEF 坐标:
手拿把掐,没有问题。
接下来我们要应用最小二乘法来根据 GPS 数据估计车辆的运动轨迹,我们算法思路如下
首先进行数据预处理,对于每个时刻t,利用 find(~isnan(PRN(:, t))) 筛选出有效卫星测量,这个很重要,一定要把 NAN (伪距缺失)去掉再做,首先从数学层面来讲,最小二乘法不支持无效数值计算,不然无法求逆,并且偏导数的计算要依赖于所有有效卫星的几何关系,缺失数据会破坏空间几何约束,再就是从噪音层面来讲,NaN的本质可能是信号丢失(隧道遮挡)、多路径干扰(高楼反射)或接收机故障,这些噪音不剔除,那还玩个屁。
然后我们选取线性化参考点 X_{ref}
其中 (x_0, y_0, z_0) 是已知的参考坐标, b_0 初值设为 0
再构建模型 h^i 和雅可比矩阵 H(i,\cdot)
对于第i 颗卫星,先计算参考点与卫星之间的距离:
则每个卫星的理论伪距模型为
其中 x, y, z 是接收机的位置坐标, b 是接收机时钟偏移, \bigl(x_{\mathrm{sat}}^i,\; y_{\mathrm{sat}}^i,\; z_{\mathrm{sat}}^i\bigr) 表示第 i 颗卫星的坐标。
根据之前的 \texttt{range\_i} 定义,因此我们可知:
则有
对应代码:
h(i) = range_i + Xref(4);接下来我们的任务是找到测量矩阵 H(i,1\!:\!4) ,测量矩阵的定义如下
我们对这些分量依次求偏导
综上所述,雅可比矩阵H 的每一行在代码中的计算公式为:
对应代码如下:
%----(3) H 矩阵的第 i 行(对x,y,z,b的偏导)----
% partial wrt x
H(i,1) = dx / range_i;
% partial wrt y
H(i,2) = dy / range_i;
% partial wrt z
H(i,3) = dz / range_i;
% partial wrt b
H(i,4) = 1;最后构造残差向量 \mathbf{z}:
如果问题是线性的,那么很简单直接如下所示
但是我们的情况是非线性的,因此有:
其中x_0 是 城市中心点, y 是GPS测量值,是PRN的一个列向量
在代码里等效实现为:
z = Y - h + H * [xyz_P0'; 0];最小二乘解算\hat{\mathbf{X}}:
在代码里等效实现为:
Xest(:, t) = pinv(H) * z;这得到估计的接收机位置(\hat{x}, \hat{y}, \hat{z}) 和时钟偏移\hat{b}。
计算精度稀释因子 DOP
如果闲着没事干,可以评估卫星几何结构对定位精度的影响,计算 DOP:
在代码里等效实现为:
DOP(t) = sqrt(trace(inv(H'*H)));展示其结果为:
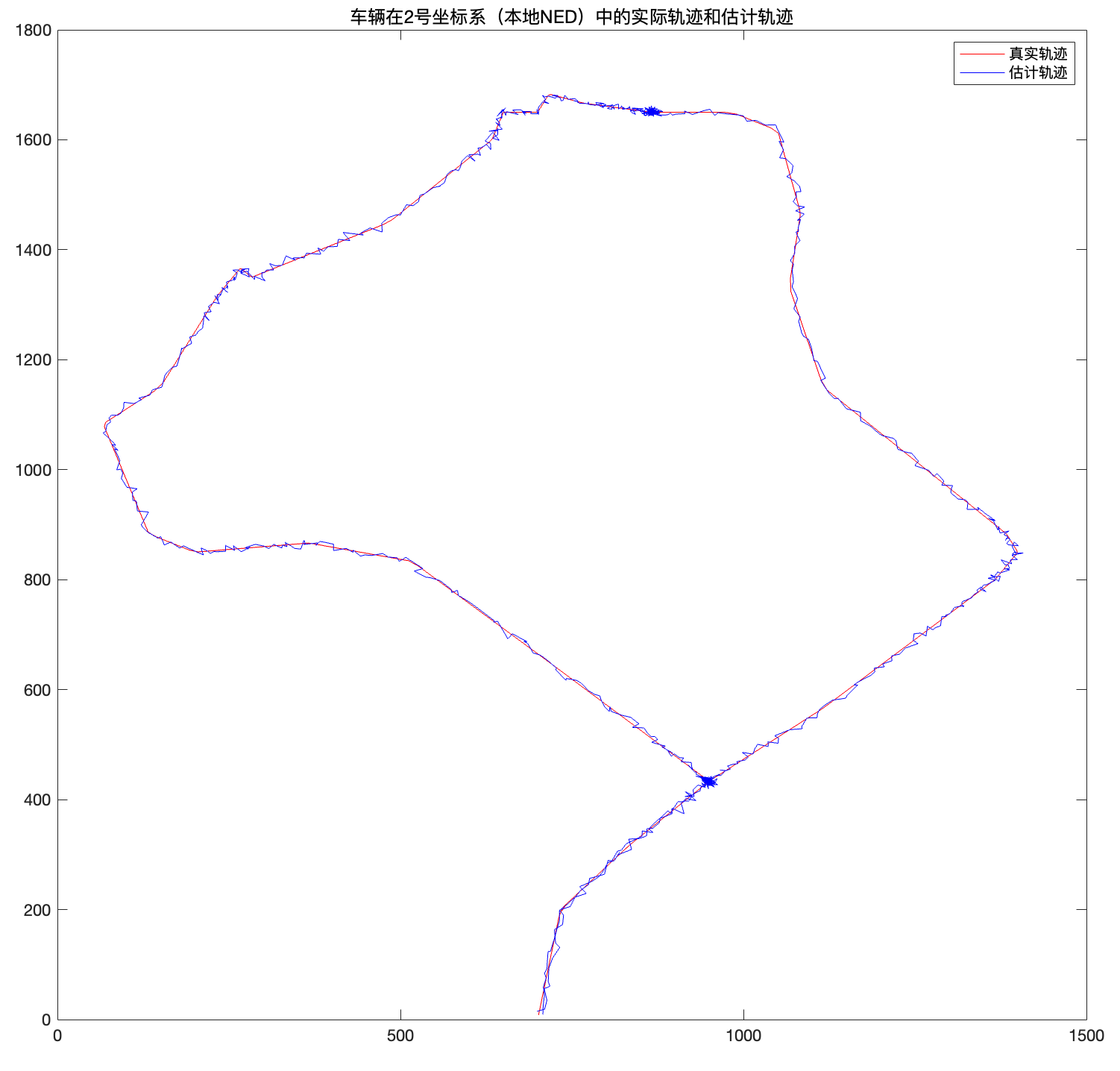
接下来我们更换 GPS 数据来模拟干扰(增加测量噪声的方差)和多路径效应(在一个或多个GPS测量中引入偏差),并且研究算法的鲁棒性(均方误差随误差幅度的变化)
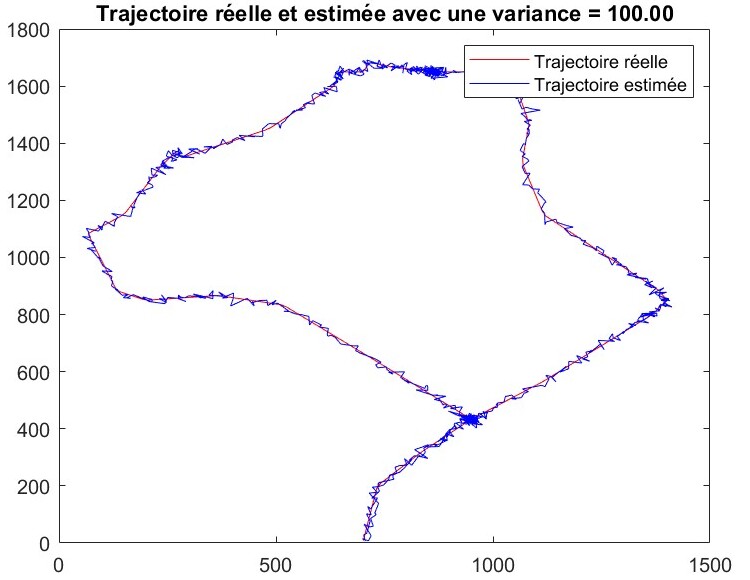
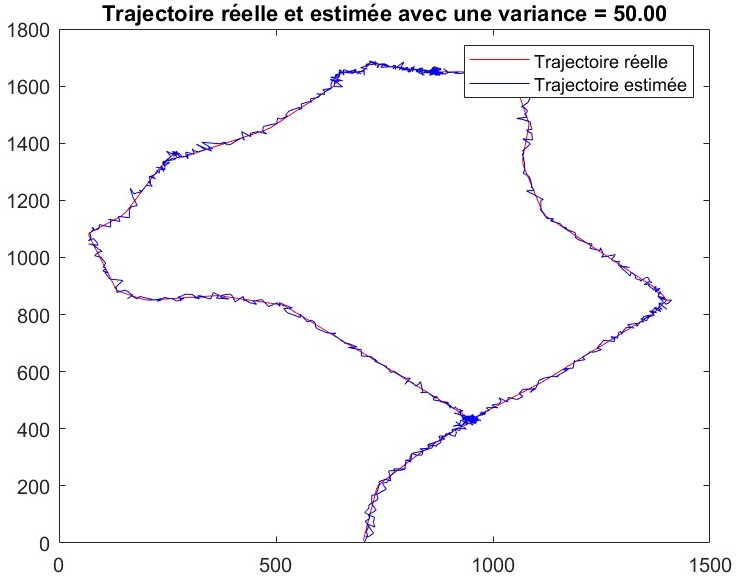
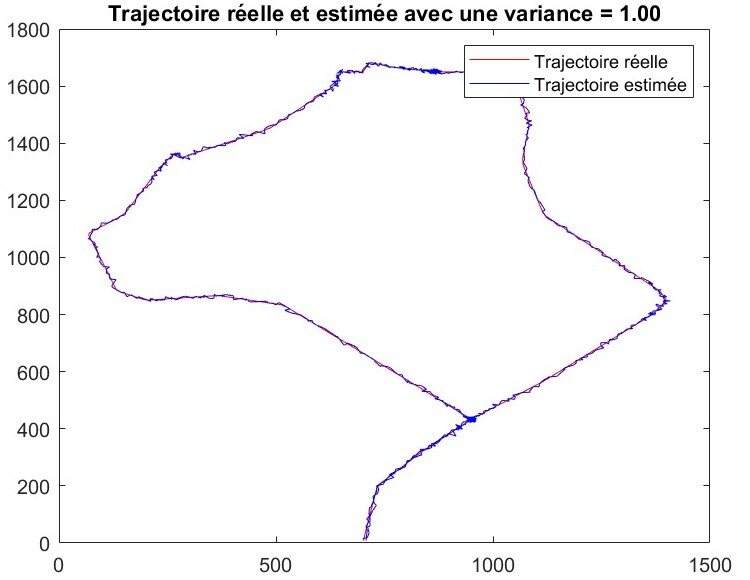
真实轨迹与添加干扰后的估计轨迹
这些图展示了在 GPS 伪距中加入高斯噪声(方差为 1、50 和 100)后的情况。在方差较小(1)的情况下,估计轨迹(蓝色)仍然与真实轨迹(红色)非常接近,仅出现小范围的局部波动。当噪声方差增加到 50 时,估计轨迹沿途开始出现更明显的扰动。最后,当方差增大到 100 时,这些误差变得更加突出,表明噪声的增加显著降低了位置估计的精度。这种退化是由于伪距测量误差的放大,直接影响最小二乘算法的解。因此,可以看到,干扰越大,整体位置误差越高,使得估计轨迹变得不稳定,可靠性降低。
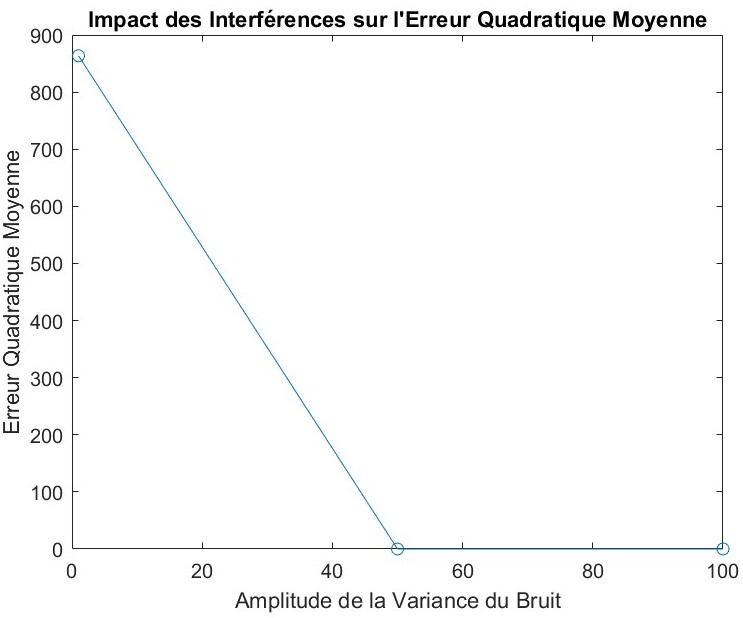
干扰对均方误差的影响
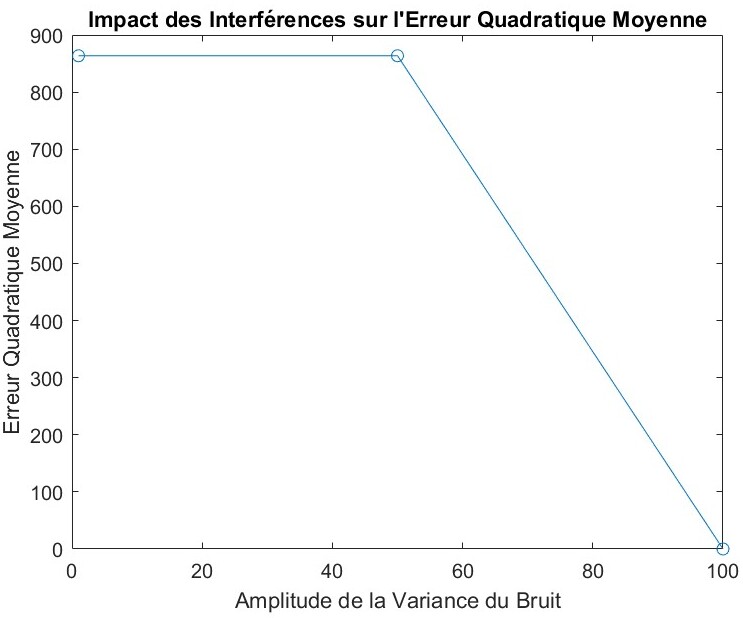
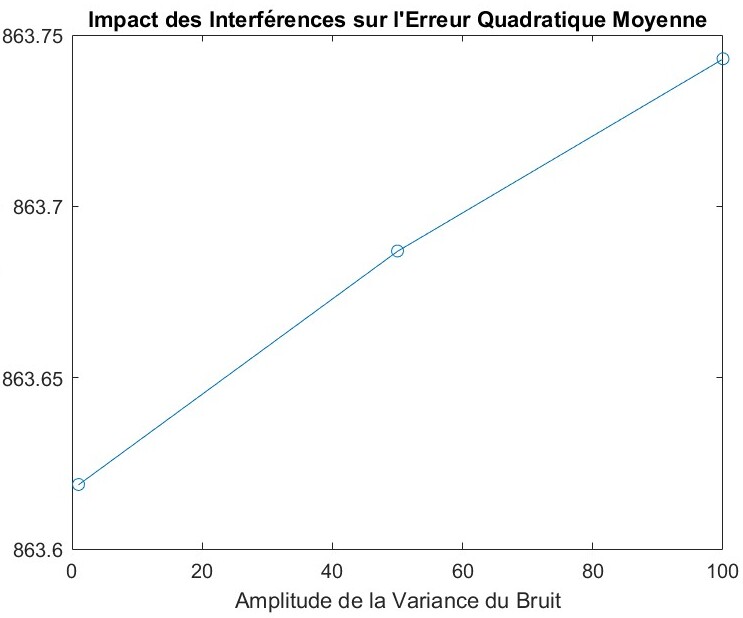
展示了均方误差如何随 GPS 伪距中加入的噪声幅度变化。通常,我们预期均方误差会随着噪声强度的增加而逐步上升,反映出估计精度的下降。
当方差为 1 时,均方误差先下降后整体趋于稳定,此时噪声强度还不足以显著破坏定位精度,算法在观测几何良好的区域能将噪声影响控制在较低水平。
当方差为 50 时,误差在较大范围内保持稳定,但在较高噪声水平时急剧下降,这个结果图绝对是错的,不过这部分不是我做的,我也不知道他怎么做的,懒得再去改
当方差为 100 时,均方误差呈现更一致的上升趋势,即噪声越大,最终估计误差越大,符合预计。
这些结果表明,尽管干扰通常会对估计精度产生负面影响,但其影响并不总是线性的。可能还有其他因素,例如卫星的几何构型或最小二乘算法的结构,会影响误差的传播方式。
在分析了干扰对轨迹估计的影响后,我们现在关注由多路径效应引入的偏差。与干扰不同,干扰在 GPS 测量中添加的是随机噪声,而多路径效应则会导致系统性偏移,使得伪距测量产生偏差,并可能在位置估计中引入持续误差。因此,我们的目标是观察偏差的引入如何影响估计轨迹的精度及均方误差。
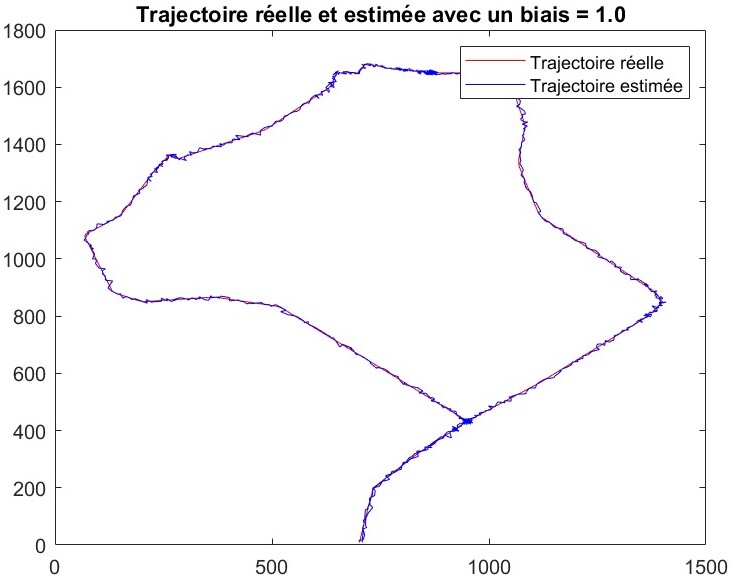
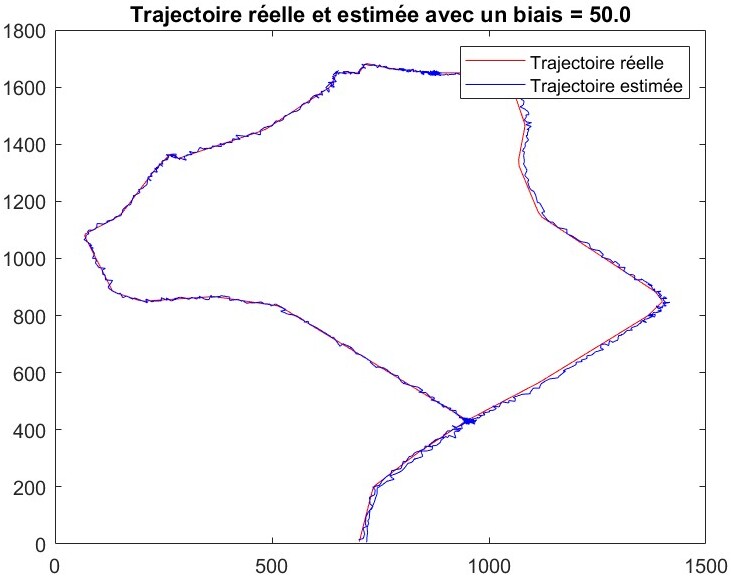
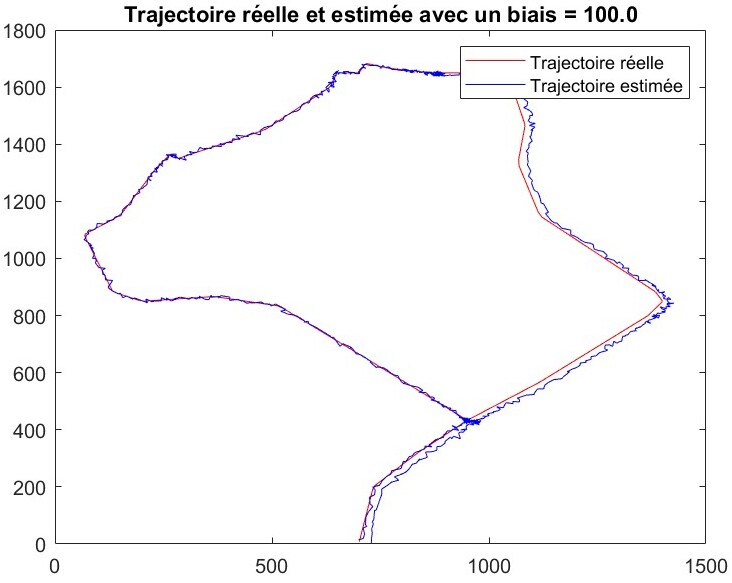
真实轨迹与加入多路径效应后的估计轨迹
当 b=1 时,估计轨迹几乎和真实轨迹重合,只有极少数路段出现细微误差,说明小偏差并不会造成显著的系统性偏移。
当 b=50 时,一些路段开始出现清晰的偏离,表明多路径偏差的累积效应导致了整体轨迹产生可观察到的系统性偏移,和随机噪声造成的“发散”不同,这里的误差表现为持续往某个方向“漂移”。
当 b=100 时,偏移进一步扩大,估计轨迹在相当大范围内脱离了真实线路,显示多路径效应不但会长期存在,而且随着偏差幅度的增长,其带来的位置误差也随之累积并变得更加明显。
与干扰不同,干扰会在轨迹周围引入随机噪声,而多路径效应则会造成稳定的、系统性的方向性偏移,这种效应在图像右下角部分尤为明显。这种现象的根本原因是多路径偏差直接影响了卫星测量的伪距,进而持续影响最小二乘算法的解。偏差越大,累积误差也越大,从而加剧了真实轨迹与估计轨迹之间的偏差。
由此可见,多路径对轨迹估计的影响与随机干扰并不相同——它会在测量中引入恒定且无法通过平均化抵消的偏差,一旦偏差值较大,就会产生大尺度且难以纠正的位置误差。
精度稀释因子 (DOP)
我们将介绍精度稀释因子( DOP )在GPS定位中的作用及其细分子指标,从而不同角度反映定位精度。我们先根据 位置估计误差 和 误差协方差矩阵及其迹 来推导几何精度因子公式。
从 位置估计误差 (1) 推导 位置误差协方差矩阵 (2)\Sigma_{\Delta X \Delta X}
位置估计误差:
误差协方差矩阵及其迹:
在假设噪声满足零均值且协方差为 σ^2I 的条件下,误差的协方差矩阵为
将公式(1)代入上式,我们有:
由于\mathbb{E}[\,w\,w^T\,] = \sigma^2 I,可进一步简化得到:
继续化简为:
接下来,我们已知位置误差的均方值为协方差矩阵的迹,即
将上式代入得到:
取平方根后,得到位置估计的均方根误差 (RMSE) 为:
几何精度因子 DOP 定义为:
替换到上式中,于是立刻得到如下关系式:
这表明,最终的定位均方误差 (RMSE) 会受到卫星星座与接收机几何关系的放大/缩小,该几何放大系数正是 \mathrm{DOP}(精度稀释因子)。对于给定的测量噪声标准差\sigma,定位均方误差不仅由噪声决定,还会受到卫星几何结构的影响。换句话说,如果某一时刻卫星分布较差(即\mathrm{DOP} 较大),那么即使噪声较小,最终的 RMSE 也会增大,导致定位精度下降。
在 MATLAB 中,针对每个时刻 t,DOP 可通过如下代码计算:
DOP(t) = sqrt(trace(inv(H' * H)));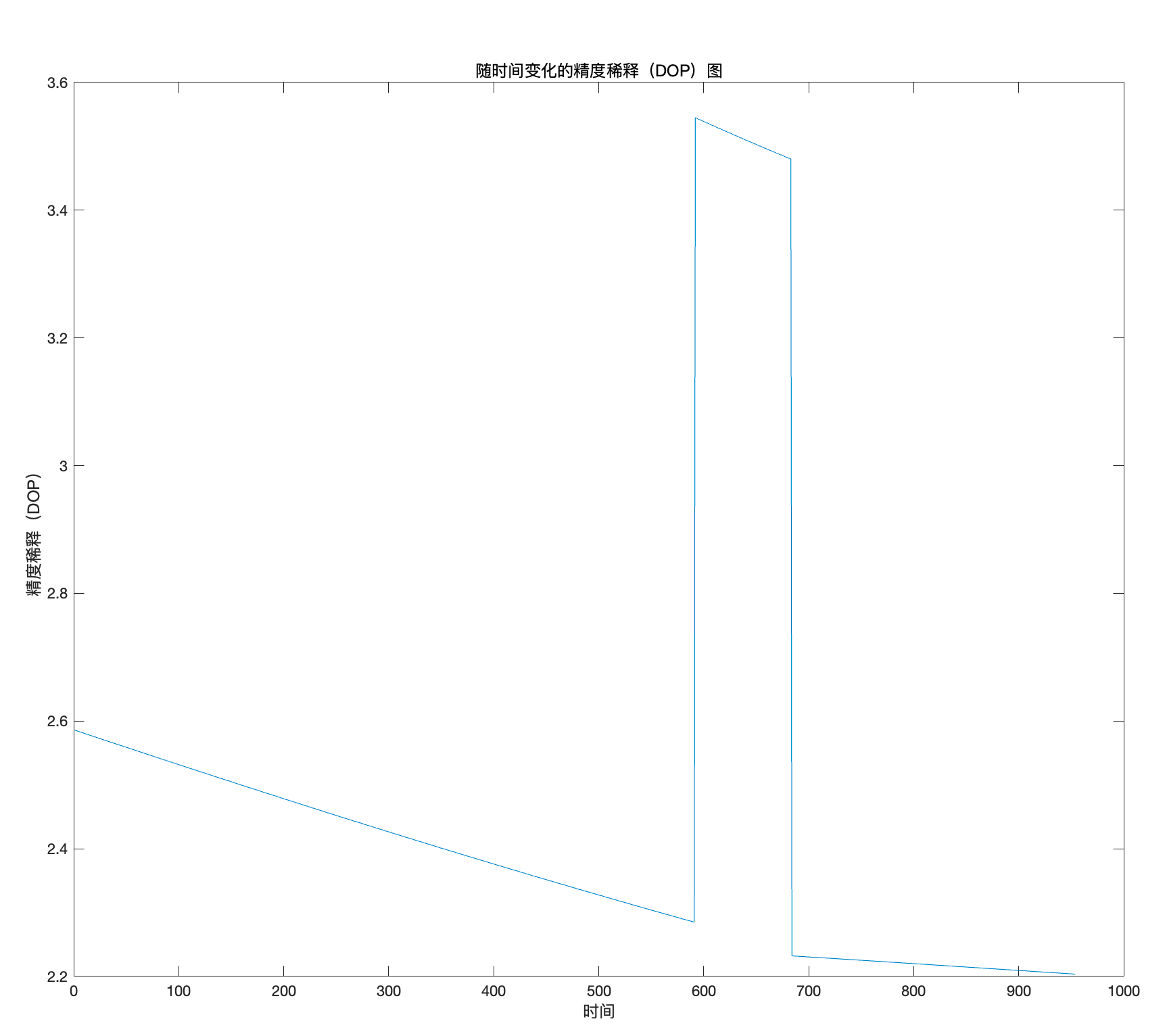
将所有时刻的 DOP 值绘制成曲线后,可以观察到当某些时刻卫星测量条件变差时,DOP 值会显著增大,这与估计轨迹的偏差通常呈正相关关系,从而验证了 DOP 的合理性。
为了进一步量化定位误差,我们可以根据不同的需求将DOP 细分为以下几种:
位置精度稀释因子 ( PDOP ):
当我们只关心三维位置估计(忽略接收器时钟偏移)时,可以从矩阵 \tilde{H}_t = (H_t^T H_t)^{-1} 的左上3 \times 3 分块中提取对角元素,其定义为
PDOP = \sqrt{\tilde{H}_t(1,1) + \tilde{H}_t(2,2) + \tilde{H}_t(3,3)}这里, PDOP 反映了位置参数受到测量噪声放大后的误差水平。
水平精度稀释因子 ( HDOP ) 和垂直精度稀释因子 ( VDOP ):
如果需要区分水平面和垂直方向上的定位精度,则需要将测量模型转换到局部坐标系(例如 NED 坐标系)。步骤如下:
首先,将卫星和接收机的 ECEF 坐标转换为 NED 坐标
对转换后的数据进行线性化,得到局部坐标系下的测量矩阵 H_t^{(NED)}
计算其逆协方差矩阵
水平精度稀释因子(水平方向上定位的不确定性)定义为
垂直精度稀释因子(垂直方向上的定位精度)则为
这种细分非常有用:当卫星在天空中的分布较为均匀时, PDOP 较低,说明整体定位精度较好,而如果某一方向的卫星分布不均(例如只有少量卫星位于低空或靠近同一方向),则相应的 HDOP 或 VDOP 会较高,提示该方向上的定位误差可能较大。
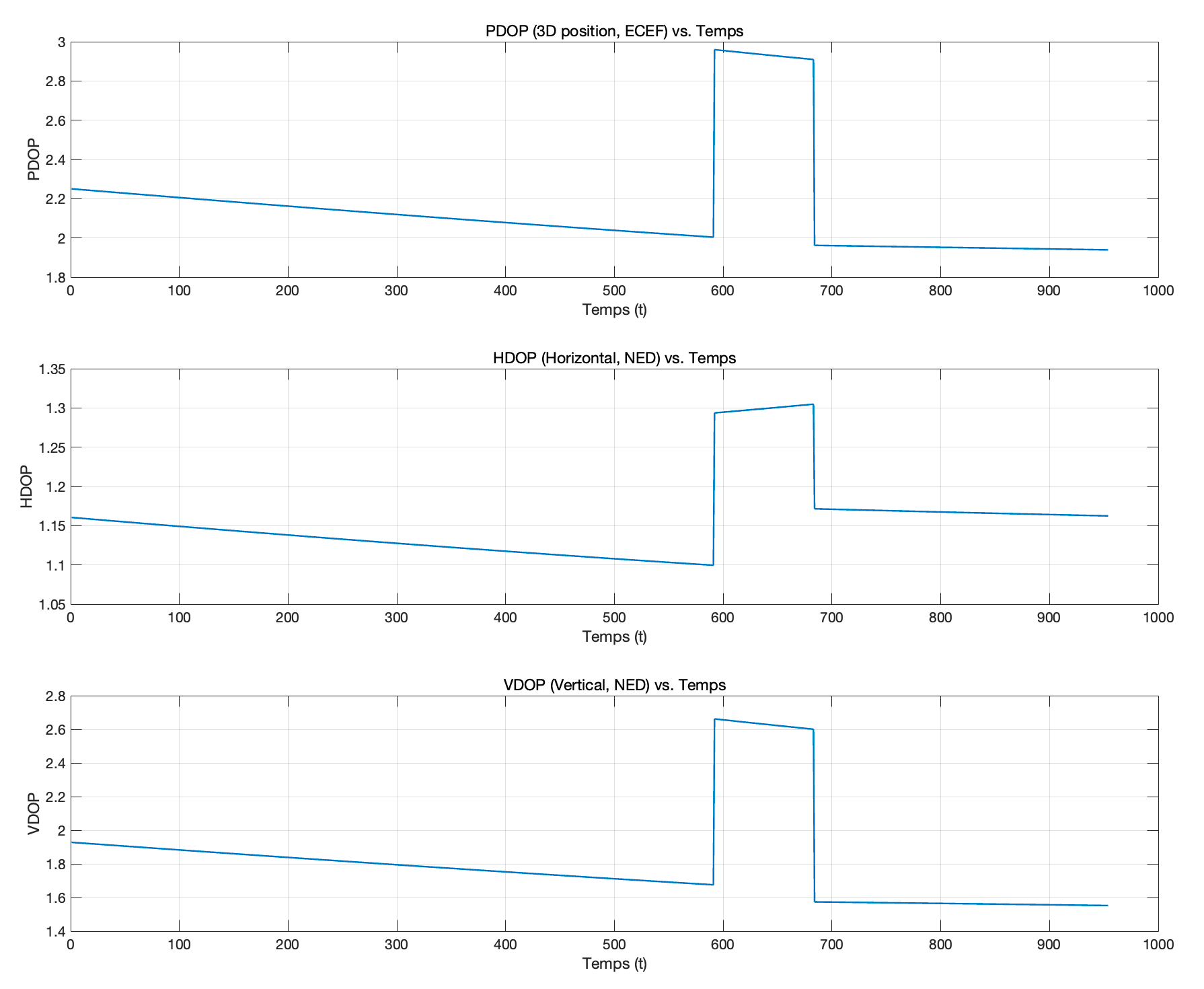
从图上可见, PDOP 、 HDOP 和VDOP 三条曲线都在同一时刻出现了显著的突变,其他时段变换则相对平滑。
在最开始的时候, PDOP 、 HDOP 和VDOP 均呈现下降趋势,说明这段时间里可用卫星的几何分布在不断优化,三维定位、水平定位及垂直定位的精度稀释因子都在变小。当曲线出现向上的跳变意味着卫星分布突然变差,比如可能有一颗或多颗关键卫星数据丢失,导致定位误差被明显放大。再往后随着新的卫星引入正确且更优的几何分布,使接收机可以得到更稳固的空间定位约束, DOP 水平因此迅速改善,并趋于稳定。
PS: 最后这里其实有一些问题,应该是 计算公式错了,但是思路大差不差,结果图的反映也符合预期,我不搞导航方向,不想再细研究了。
完整代码
close all, clear all, clc
%% Question 2
load trajectoire_TP % 加载GPS轨迹数据文件 "trajectoire_TP"
latitude = deg2rad(44 + 48/60); % 将纬度从度和分转换为弧度,44°48' 北纬
longitude = -deg2rad(0 + 35/60); % 将经度从度和分转换为弧度,0°35' 西经,西经为负值
altitude = 0; % 海拔高度为0 代表坐标的z轴是0
llh = [latitude, longitude, altitude];
xyz_P0 = llh2xyz(llh);
disp('在参考坐标系1(ECEF)中的参考点P0的坐标:');
disp(['X : ', num2str(xyz_P0(1))]); % 显示参考点P0的X坐标
disp(['Y : ', num2str(xyz_P0(2))]); % 显示参考点P0的Y坐标
disp(['Z : ', num2str(xyz_P0(3))]); % 显示参考点P0的Z坐标
%% Question 3
load('donnees_GPS_TP.mat'); % 加载GPS卫星数据文件
cla = cos(latitude); % 计算纬度的余弦
sla = sin(latitude); % 计算纬度的正弦
clon = cos(longitude); % 计算经度的余弦
slon = sin(longitude); % 计算经度的正弦
M = [-sla*clon, -slon, -cla*clon; % 构建旋转矩阵M,用于从ECEF转换到局部NED坐标系
-slon*sla, clon, -cla*slon;
cla, 0, -sla];
T = size(XYZsat,3);
for t = 1:T % 遍历每个时间点
ind = find(~isnan(PRN(:, t))); % 找出当前时刻 t 所有非 NaN 测量的卫星索引
Y = PRN(ind, t); % 取出对应的伪距测量值
nb_mes = length(ind); % 当前测量值
h = zeros(nb_mes, 1); % 存放每条测量对应的模型值 h(i)
H = zeros(nb_mes, 4); % 初始化测量矩阵H,用于后续线性化
for i = 1:nb_mes
Xref = [xyz_P0(1); xyz_P0(2); xyz_P0(3); 0]; % (x0,y0,z0,b0)
%----(1) 计算当前卫星到参考点的几何距离-----
dx = Xref(1) - XYZsat(ind(i),1,t);
dy = Xref(2) - XYZsat(ind(i),2,t);
dz = Xref(3) - XYZsat(ind(i),3,t);
range_i = sqrt(dx^2 + dy^2 + dz^2);
%----(2) 模型值 h^i = range_i + b_est ----
h(i) = range_i + Xref(4);
%----(3) H 矩阵的第 i 行(对x,y,z,b的偏导)----
% partial wrt x
H(i,1) = dx / range_i; % ∂h/∂x
% partial wrt y
H(i,2) = dy / range_i; % ∂h/∂y
% partial wrt z
H(i,3) = dz / range_i; % ∂h/∂z
% partial wrt b
H(i,4) = 1; % ∂h/∂b
end
DOP(t) = sqrt(trace(inv(H' * H))); % 计算精度稀释因子DOP
% 构造观测残差z,将观测值与预测值和初始估计值差计算出来
z = Y - h + H * [xyz_P0'; 0];
% Application de la méthode des moindres carrés
% 使用最小二乘法估计位置和偏差,结果存储在Xest中
Xest(:, t) = pinv(H) * z;
% 将估计的ECEF坐标转换为局部NED坐标
Xloc_est(:, t) = inv(M) * (Xest(1:3, t) - xyz_P0');
end
% 绘制3D估计轨迹
figure, plot3(Xest(1, :), Xest(2, :), Xest(3, :));
title('车辆在1号坐标系(ECEF)中估计轨迹的3D图形')
% 绘制局部NED坐标系下的真实轨迹和估计轨迹
figure
plot(Xloc(1, :), Xloc(2, :), 'r'), hold on % 绘制真实轨迹
plot(Xloc_est(1, :), Xloc_est(2, :), 'b') % 绘制估计轨迹
title('车辆在2号坐标系(本地NED)中的实际轨迹和估计轨迹')
legend('真实轨迹', '估计轨迹') % 添加图例
% 绘制DOP随时间的变化
figure
plot(DOP)
title('随时间变化的精度稀释(DOP)图')
xlabel('时间')
ylabel('精度稀释(DOP)')
%%
% 初始化数组,用于存储每个历元的 PDOP、HDOP、VDOP
PDOP_3D = zeros(1, T); % 三维位置PDOP (不含钟偏)
HDOP_2D = zeros(1, T); % 水平DOP
VDOP_1D = zeros(1, T); % 垂直DOP
for t = 1:T
%----------------------------------------------------------------------
% 1) 与 Question 3 类似: 找到可用卫星并构造几何矩阵 H_temp (ECEF)
%----------------------------------------------------------------------
ind = find(~isnan(PRN(:, t)));
Y = PRN(ind, t);
nb_mes = length(ind);
% 若可用卫星数 < 4,则最小二乘解会退化;这里直接跳过
if nb_mes < 4
PDOP_3D(t) = NaN; HDOP_2D(t) = NaN; VDOP_1D(t) = NaN;
continue
end
h = zeros(nb_mes, 1);
H_temp = zeros(nb_mes, 4);
for i = 1:nb_mes
% 计算该颗卫星到参考点 P0 的几何距离 (忽略b或者b=0,仅用于构造H)
d = sqrt( (xyz_P0(1) - XYZsat(ind(i),1,t))^2 + ...
(xyz_P0(2) - XYZsat(ind(i),2,t))^2 + ...
(xyz_P0(3) - XYZsat(ind(i),3,t))^2 );
% 填充测量敏感度 H_temp (前三列:位置; 第4列:钟偏)
H_temp(i,1:3) = (xyz_P0(1:3) - XYZsat(ind(i),:,t)) / d; % ∂h_i/∂(x,y,z)
H_temp(i,4) = 1; % ∂h_i/∂b
end
%----------------------------------------------------------------------
% 2) 计算 ECEF 下的 3D PDOP:
% 先做 (H_temp' * H_temp)^(-1) => 4×4, 然后只取前三对角来算PDOP
%----------------------------------------------------------------------
H_tilde_ecef = inv(H_temp' * H_temp);
PDOP_3D(t) = sqrt( H_tilde_ecef(1,1) + ...
H_tilde_ecef(2,2) + ...
H_tilde_ecef(3,3) );
%----------------------------------------------------------------------
% 3) 为了得到“正宗”的 HDOP、VDOP:在 NED 坐标系下重构几何矩阵
% H_ned 的大小仍然是 nb_mes×4,但前三列要乘以 inv(M)
%----------------------------------------------------------------------
H_ned = H_temp;
% H_temp(:,1:3) 是 nb_mes×3, M 是 3×3
% localNED = inv(M) * ecef => 下面用行列式转置处理
H_ned(:,1:3) = ( inv(M) * (H_temp(:,1:3)') )';
% 再求 (H_ned^T * H_ned)^(-1)
H_tilde_ned = inv(H_ned' * H_ned);
%----------------------------------------------------------------------
% 4) 在 NED 坐标下, 提取 HDOP = sqrt( N+E 对角和 ), VDOP = sqrt( D 对角 )
% 同理若要 PDOP (N,E,D), 就取前三对角元素之和
%----------------------------------------------------------------------
HDOP_2D(t) = sqrt( H_tilde_ned(1,1) + H_tilde_ned(2,2) );
VDOP_1D(t) = sqrt( H_tilde_ned(3,3) );
end
%--------------------------------------------------------------------------
% 绘制 PDOP / HDOP / VDOP
%--------------------------------------------------------------------------
figure
subplot(3,1,1), plot(PDOP_3D, 'LineWidth',1.2), grid on
title('PDOP (3D position, ECEF) vs. Temps')
xlabel('Temps (t)'), ylabel('PDOP')
subplot(3,1,2), plot(HDOP_2D, 'LineWidth',1.2), grid on
title('HDOP (Horizontal, NED) vs. Temps')
xlabel('Temps (t)'), ylabel('HDOP')
subplot(3,1,3), plot(VDOP_1D, 'LineWidth',1.2), grid on
title('VDOP (Vertical, NED) vs. Temps')
xlabel('Temps (t)'), ylabel('VDOP'