背景简介

粒子滤波是一种基于蒙特卡洛方法的贝叶斯估计工具，适用于那些非线性且噪声不符合高斯分布的动态系统。简单来说，粒子滤波方法通过生成大量的“粒子”（每个粒子代表目标可能的位置），然后利用雷达观测数据不断更新这些粒子，最终以概率的方式估计出目标的真实位置。

粒子滤波应用于目标跟踪主要解决的问题是：如何利用带噪声的雷达测量数据来估计移动目标的真实运动轨迹。

在我们的目标跟踪场景中，雷达作为传感器发射非常短的脉冲信号，这些脉冲以光速在大气中传播。当脉冲遇到目标时，部分信号会被反射回雷达天线。经过一系列处理后，雷达能够计算出两个关键信息：

• 目标与雷达之间的距离r

• 目标所在方向与参考轴之间的角度\theta

目标与雷达的距离可以通过信号来回传播的时间间隔\Delta t 计算出来，计算公式为

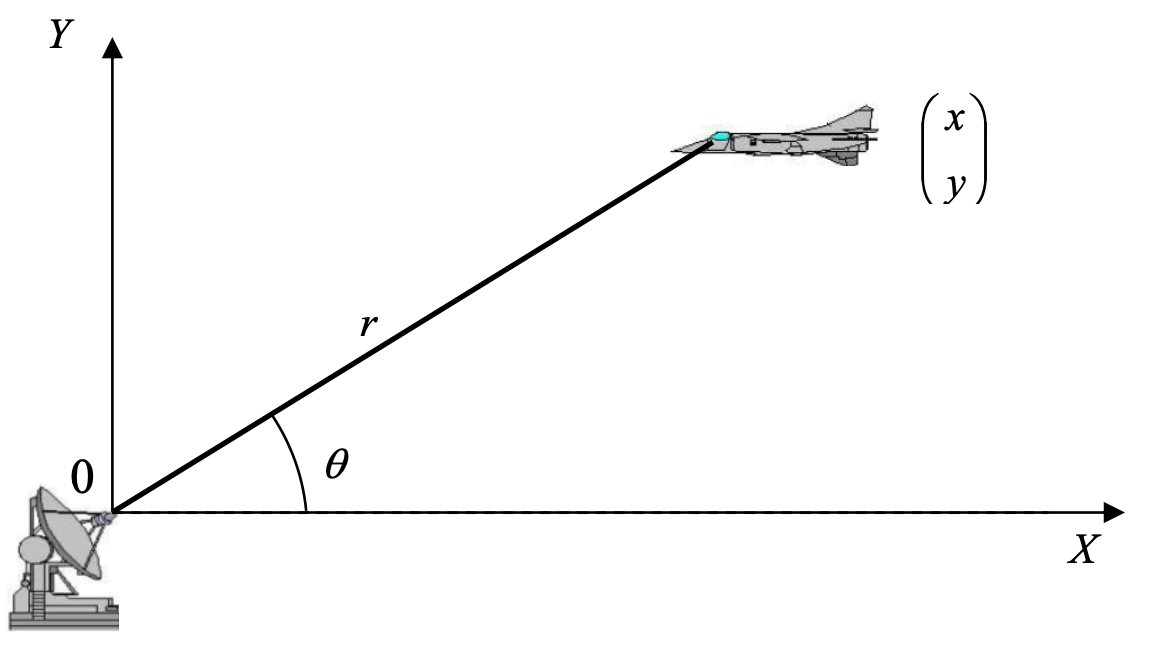
• 其中c 表示光速。图示中，雷达被固定在坐标系原点(0,0)。

我们的任务是通过带有噪声的雷达测量数据，即观测到的角度\theta^m(t) 和距离r^m(t)，来恢复目标随时间变化的真实位置(x(t), y(t))。因此观测模型可以写成

• 其中v_r(t) 和v_\theta(t) 分别代表测量中加入的噪声。

符号说明

真实距离r(t)
这里r(t) 表示目标与雷达之间的实际几何距离。由于目标的真实位置是由坐标(x(t), y(t)) 给出的，我们可以利用勾股定理来计算实际距离，公式为

真实角度\theta(t)
\theta(t) 表示从雷达视线轴到目标所在方向的真实角度，同样可以根据目标坐标得到，计算公式为

观测向量\mathbf{z}(t)
为了同时表示距离和角度的测量值，我们将带噪声的观测数据合并成一个向量

因此，带噪声的观测模型也可以写成

• 在这里， v_r(k) 和v_\theta(k) 都是假设为均值为0、方差分别为\sigma_r^2 和\sigma_\theta^2 的高斯噪声。

另外，为了便于处理，我们假设每次雷达测量之间的时间间隔是固定的，用T 表示。这意味着我们只在离散的时间点t_k = kT（其中k \geq 0）对目标的位置进行估计。为了简化表达，后续的符号会写成

数学建模

根据以上背景信息，我们马上就打算实现粒子滤波器的Matlab 函数，但在此之前，我们要先建立一个描述目标运动状态的模型。

首先，我们假设目标不会做剧烈机动，也就是说它没有明显的大加速度。这样，我们可以把目标的加速度看作是白噪声:

• 其中 u_x(k) 和u_y(k) 分别代表x 和y 方向上的随机加速度，并且满足：

在这种假设下，我们需要选择一个最合适的状态向量来描述和估计目标的运动。直观的做法是同时考虑目标的位置和速度。因此，我们设定状态向量为

接下来，我们利用泰勒展开来推导目标在两个连续时刻之间的位置和速度之间的关系。假设两次测量之间的时间间隔为T，那么对于x 方向来说，泰勒展开给出：

对位置x(k)：

因为我们用白噪声来代替加速度，即\ddot{x}(k-1)=u_x(k-1)，所以可以写成：

对速度\dot{x}(k)：

同样，将\ddot{x}(k-1) 替换为u_x(k-1) 得：

对于y 方向的情况，过程一样：

对位置y(k)：

用\ddot{y}(k-1)=u_y(k-1) 替换后为：

对速度\dot{y}(k)：

替换后得：

上面公式看起来乱七八糟的一看就困，所以更直观一点:

目标位置

目标速度

将以上x 和y 方向的关系整合在一起，就可以得到状态模型的矩阵表达式

可得:

因此，状态转移矩阵\Phi(k, k-1) 和控制（或输入）矩阵G(k) 分别为：

状态转移模型就构建完毕了，既考虑了目标位置的更新，也考虑了速度的变化，同时把由于机动产生的随机扰动用白噪声建模。

下面是函数 matrices_etat 的代码：

function [Phi, G] = matrices_etat(T)
    % 计算状态转移矩阵 Phi (4x4)
    Phi = [1, T, 0, 0;
           0, 1, 0, 0;
           0, 0, 1, T;
           0, 0, 0, 1];
    
    % 计算加速度影响矩阵 G (4x2)
    G = [0.5*T^2, 0;
         T,       0;
         0, 0.5*T^2;
         0,       T];
end

接下来，给出计算平面上一点 (x,y) 到雷达之间的几何距离和角度的两个函数。理论上，距离和角度分别为

在 Matlab 中，我们使用 atan2 函数来计算角度（避免象限问题）。

函数 fonction_r 的代码如下：

function r = fonction_r(x, y)
    % 计算几何距离 r = sqrt(x^2 + y^2)
    r = sqrt(x^2 + y^2);
end

函数 fonction_theta 的代码如下：

function theta = fonction_theta(x, y)
    % 计算角度，使用 atan2 可处理四象限
    theta = atan2(y, x);
end

最后，我们尝试求解似然函数的表达式，我们直接给出结论，为如下形式:

下面我们给出证明

首先，由于测量误差服从高斯分布，我们可以利用高斯分布的概率密度函数来描述在给定目标真实状态下，观测值出现的概率。对于一个观测值 x ，其服从均值为 \mu 、方差为 \sigma^2 的高斯分布时，概率密度函数写作

在本实验中，雷达测量得到的观测向量为

其中 r^m(t) 表示实际测得的距离， \theta^m(t) 表示实际测得的角度。它们由真实的距离和角度加上各自的噪声构成，即

由于我们知道真实距离和角度分别可由状态中目标的坐标计算得到

更直观的表示:

因此，我们可以在离散时刻 k 写成

• v_r(k) \sim \mathcal{N}(0, \sigma_r^2) 是距离测量误差

• v_\theta(k) \sim \mathcal{N}(0, \sigma_\theta^2) 是角度测量误差

测量值的概率取决于这些噪声的分布，因此似然函数的表达式来自于噪声的概率密度函数。

距离的似然函数

接下来，我们利用上述高斯分布的概率密度函数来构造似然函数。对距离部分，测量值 r^m(k) 是由真实距离 h_r(x(k), y(k)) 加上测量误差 v_r(k) 得到的：

如果我们认为噪声 v_r(k) \sim \mathcal{N}(0, \sigma_r^2) ，则在状态 \underline{\mathbf{x}}(k) 下，测量值 r^m(k) 出现的概率密度为

这评估在目标状态 \underline{\mathbf{x}}(k) 下，实际测量值 r^m(k) 偏离理论值 h_r(\underline{\mathbf{x}}(k)) 的可能性。偏离越小，似然值越大。

角度的似然函数

同样，对于角度部分，测量值 \theta^m(k) 是由真实角度 h_\theta(x(k), y(k)) 加上测量误差 v_\theta(k) 得到的：

同样假设 v_\theta(k) 服从均值为 0 、方差为 \sigma_\theta^2 的高斯分布，则角度的概率密度函数为

这评估在目标状态 \underline{\mathbf{x}}(k) 下，实际测量值 \theta^m(k) 偏离理论值 h_\theta(\underline{\mathbf{x}}(k)) 的可能性。

组合似然函数：

对于距离测量和角度测量分别有

由于距离和角度的噪声相互独立，整个测量的似然函数就是这两部分概率密度的乘积:

展开为:

下面我们编写 Matlab 函数 vraisemblance，使用函数 fonction_r 和 fonction_theta，并且使用以下输入量来计算输出

即输入参数为 目标位置 (x,y) ，带噪测量值 z_r 和 z_\theta 以及噪声标准差 \sigma_r 和 \sigma_\theta

function p = vraisemblance(x, y, z_r, z_theta, sigma_r, sigma_theta)
    % 使用 fonction_r 和 fonction_theta 计算真实的距离和角度
    r = fonction_r(x, y);      % 真实距离
    theta = fonction_theta(x, y);  % 真实角度
    
    % 计算距离的似然函数部分
    p_r = (1 / sqrt(2 * pi * sigma_r^2)) * exp( -((z_r - r)^2) / (2 * sigma_r^2) );
    
    % 计算角度的似然函数部分
    p_theta = (1 / sqrt(2 * pi * sigma_theta^2)) * exp( -((z_theta - theta)^2) / (2 * sigma_theta^2) );
    
    % 总的似然函数为两部分的乘积
    p = p_r * p_theta;
end

fonction_r fonction_theta vraisemblance 这三个函数实现了状态矩阵、距离和角度计算以及基于高斯噪声模型的似然函数计算。

 粒子滤波流程

粒子表示和初始化

在粒子滤波中，我们用多个粒子来代表目标状态空间中的不同假设，每个粒子就是一个状态向量\underline{\mathbf{x}} （例如包含目标的位置信息和速度信息）。在数据中，我们有一个表格，每列表示一个粒子，每行是粒子的某个状态变量（例如位置、速度等）

一开始，我们根据目标状态的先验分布随机生成一组粒子，并且赋予每个粒子相同的初始权重。每经过一个时间步，粒子滤波的主要包括以下几个步骤：

粒子的传播

对每个粒子，利用当前粒子的状态，加上随机扰动，得到下一时刻的可能状态

其中

• \Phi 是状态转移矩阵，表示时间间隔内 位置 和 速度 之间的关系

• G 是控制输入矩阵（反映噪声对状态的影响）

• \underline{\mathbf{u}}(k-1) 是模拟的加速度噪声，从高斯分布中随机生成

每个粒子通过状态转移模型产生一个新的粒子，更新状态。

计算权重

根据新时刻的测量值\underline{\mathbf{z}}(k) （包含距离和角度信息），我们对每个粒子计算一个权重（反映了粒子状态与测量值匹配的程度）

已知似然值的公式：

因此权重更新公式为

更新后，对所有粒子的权重进行归一化，使它们的总和为 1

状态估计

利用所有粒子的状态和对应的权重，可以估计当前时刻的目标状态。我们使用加权平均，得到当前时间步的状态估计

输出的状态估计值是\hat{\underline{\mathbf{x}}}(k) 加权后的粒子分布中心。

重采样

当大部分粒子的权重变得非常低时，称为粒子退化。为了防止这种情况，我们采用重采样方法。根据当前粒子的权重重新采样，权重较高的粒子更可能被重复采样，而权重低的粒子则可能被舍弃。这样可以使得重新生成的粒子表格具有均匀的权重，并更好地代表目标状态的后验概率分布。

在整个过程中，我们不断地循环以上步骤，就可以利用雷达测量数据动态地估计目标的运动轨迹。

粒子滤波编程

首先加载测量数据文件 mesures_radar.mat，供了测量数据矩阵 Z ，其中 Z(1,k) 与 Z(2,k) 分别表示第 k 个时刻的距离和角度测量值。

然后实现状态转移的 Matlab 函数 simu_modele_etat 。该函数的输入为前一时刻的状态向量\underline{\mathbf{x}}(k-1) 、状态转移矩阵\Phi(k, k-1) 、控制矩阵G(k) 以及噪声标准差 \sigma_u 。函数从高斯分布中生成加速度噪声 u ，并利用状态模型计算当前时刻的状态\underline{\mathbf{x}}(k) ，公式如下

对应代码如下

function x_current = simu_modele_etat(x_prev, Phi, G, sigma_u)
    % 生成一个可能的下一个状态
    % 产生 2x1 维的加速度噪声，标准差为 sigma_u
    u = randn(2, 1) * sigma_u;  
    % 根据状态模型更新状态
    x_current = Phi * x_prev + G * u;
end

初始化

在初始阶段，我们选取 N=1000 个粒子，并利用 trajectoire_reelle.mat 中提供的初始真实位置进行初始化。设置的参数如下：

重采样

同时使用 TP_particulaire.zip 提供的 resampling 程序进行粒子的重采样。

结合上述状态传播、权重更新、状态估计和重采样步骤，就可以利用 SIR 粒子滤波器从雷达数据中估计目标的轨迹。这种流程使得粒子滤波器在非线性、非高斯环境下依然能较好地近似目标的状态概率分布，并实现动态目标跟踪。

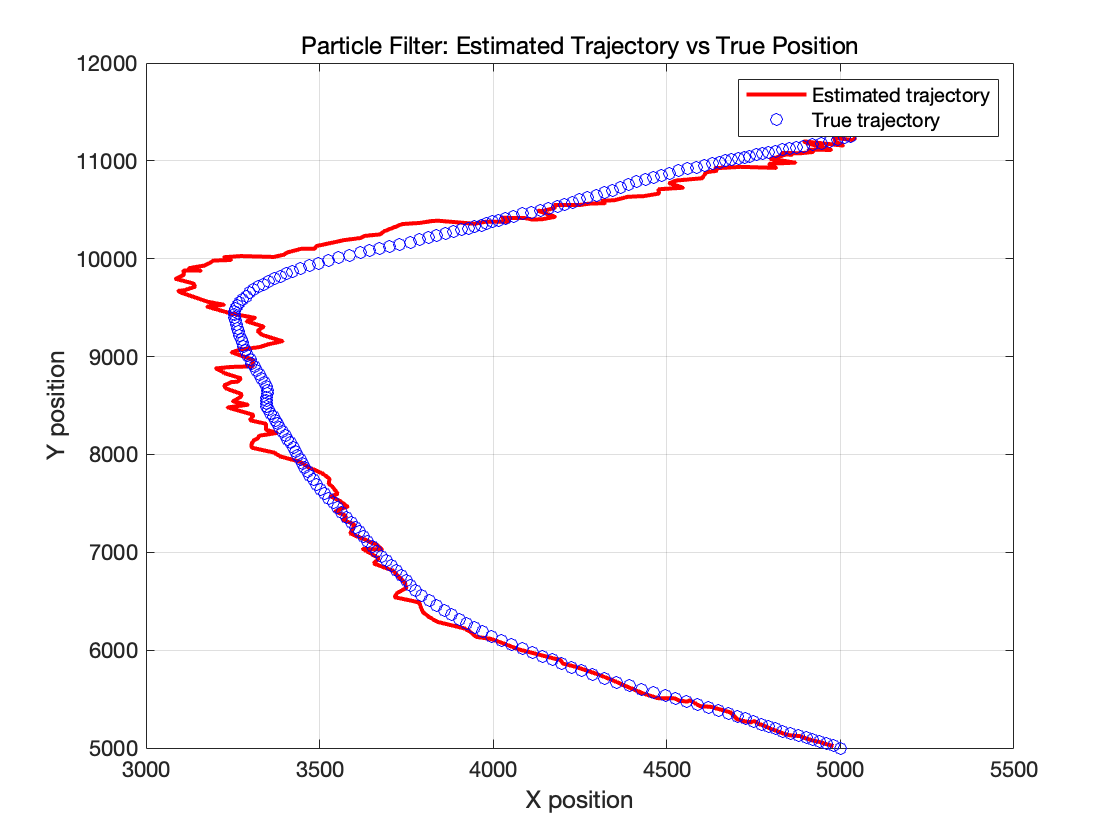
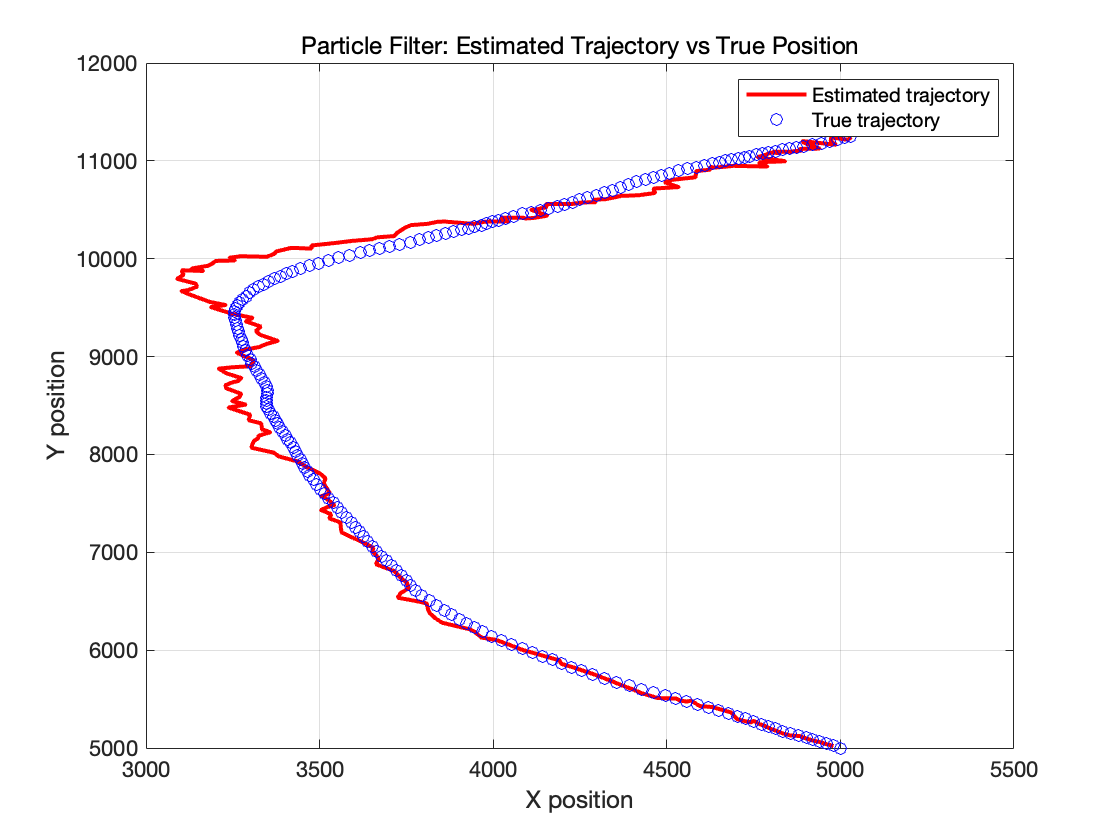
使用 N = 1000 个粒子进行粒子滤波时，我们可见滤波器估计出的目标运动轨迹能够很好的跟随真实轨迹，不过同时在某些位置出现了很大的偏差，造成这偏差的原因有以下几点:

雷达测量误差导致观测数据有噪声

• 距离测量误差：雷达测量的距离带有方差\sigma_r^2 = 50^2\text{ (m}^2\text{)} 的高斯噪声。当目标距离雷达较远时，稍小的测量偏差也会映射成更大范围的坐标估计误差。

• 角度测量误差：角度测量带有方差\sigma_\theta^2 = \left(\frac{\pi}{100}\right)^2 的噪声。雷达测量的角度偏差在几何上具有放大效应——尤其是目标处于远距离、并且真实运动带有较大转弯时，微小的角度噪声即可导致显著的位置偏离。

因此，当目标在转弯区域需要对角度进行精确捕捉时，测量噪声会在几何映射中被放大，进而拉大粒子滤波器的估计偏差。 同时，如果在某些时间步发生了粒子退化现象，那么即使后续进行重采样操作，也需要一定的迭代次数来使新粒子分布重新贴近真实轨迹，因此滤波器的估计偏差暂时增大，需要后续更多的时间步来慢慢纠正偏差。

重采样的意义

引入重采样的主要意义在于解决粒子退化问题，即粒子权重衰减问题。随着滤波器运行，部分粒子的权重会逐渐变得非常低，导致只有少数几个粒子占据绝大部分权重，而其他粒子的贡献极小，这种现象用数学公式可以表示为：

当 N_{eff} 明显低于总粒子数 N 时，说明大部分粒子的权重已经接近零，此时滤波器中只有少数粒子在起作用。引入重采样后，可以将具有较大权重的粒子复制多份，而将低权重的粒子舍弃，从而使粒子分布更集中在状态空间中概率较高的区域，有助于提高状态估计的准确性和稳定性。

没有必要在每个时间步都进行重采样，过于频繁的重采样可能导致粒子的多样性降低，丢失了对状态空间中低概率区域的探索能力。因此，通常只有当 N_{eff} 低于某个预定阈值（如代码中： N_{eff} < 0.95 \cdot N ）时，才进行重采样。这样既能避免粒子退化，又能保持足够的粒子多样性，以便更准确地捕捉目标状态的动态变化。

我们在代码中调整来直观看一下其影响:

首先只调整粒子数目，不改变其他初始值

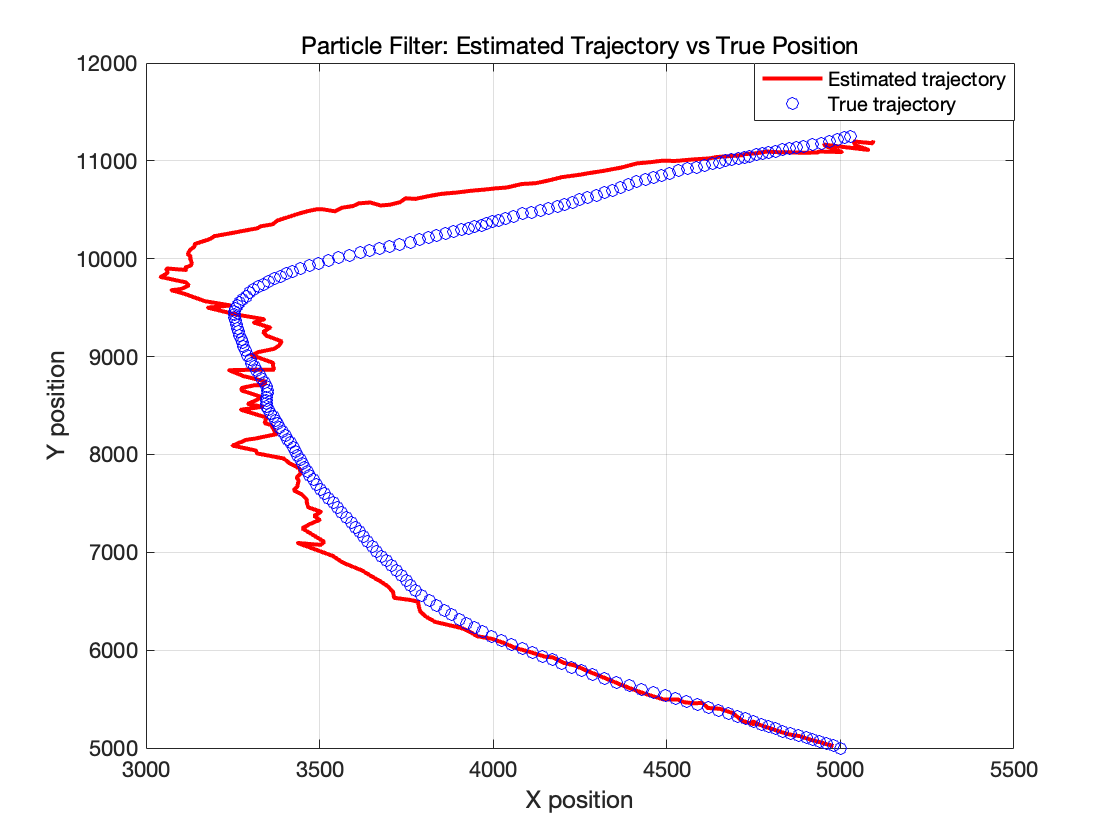
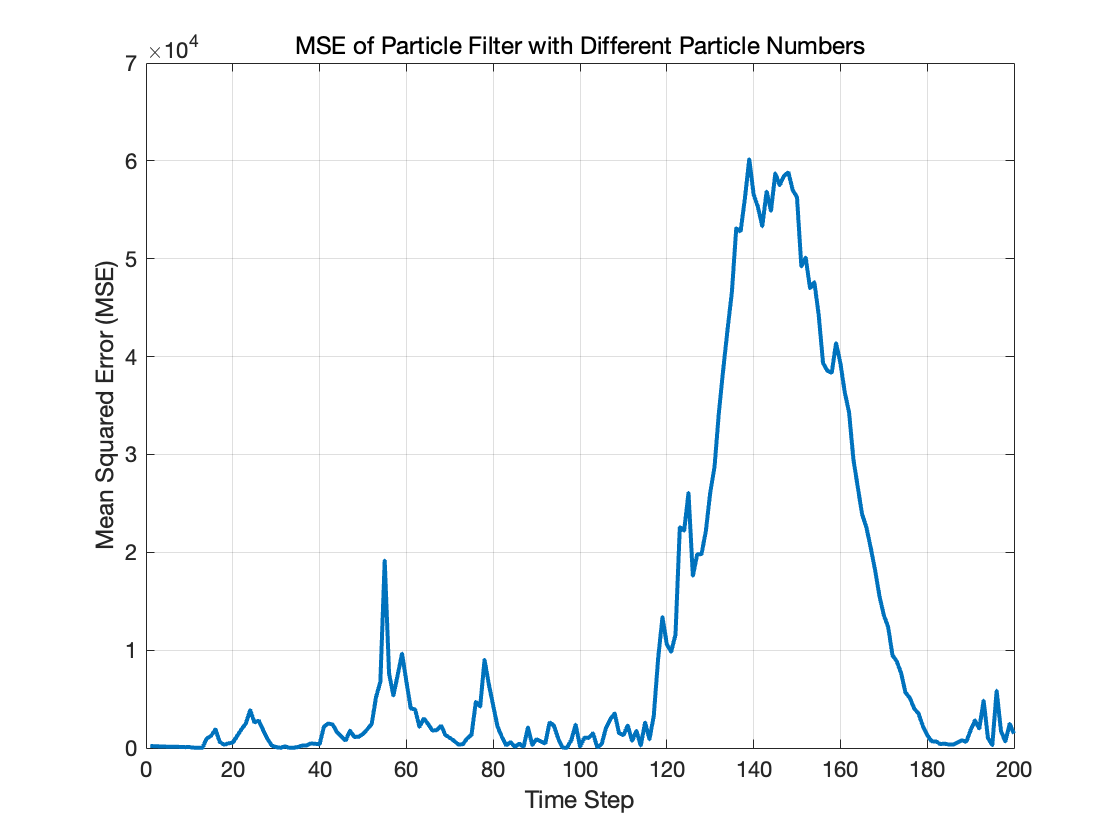
当粒子数目减少到 100 的时候，可以明显观察到滤波精度的下降，估计误差变大，这是因为粒子滤波需要足够的粒子来近似目标状态的后验分布。 在MSE图中，我们看到在 120 到 180 这个时间步内MSE非常大，表明这一阶段滤波器估计误差明显增大，这对应左图转弯机动部分，其原因还是由于粒子数量减少，采样不足导致估计的分布不能很好地近似真实状态分布。

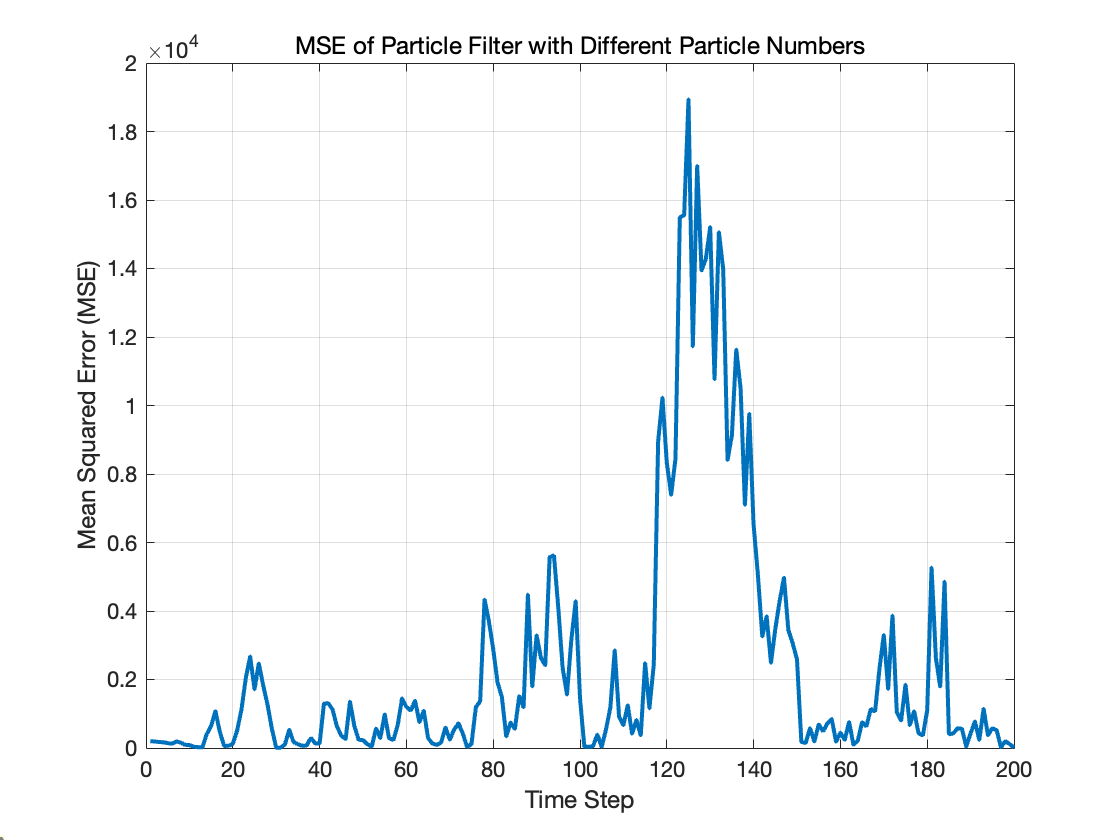
当粒子数增加到 N=10000 时，滤波估计结果与 N=1000 的情况一样，进一步增加粒子数目没有提高估计精度（减小MSE），这是因为粒子数目已经饱和，估计结果已经收敛，1000 粒子已经可以基本覆盖目标的状态空间，光靠增加粒子数目无法改变白噪声模型假设的局限性。

算法对噪声参数的敏感性

下面我们调整状态噪声和测量噪声的标准差值，并且引入无噪声数据，来更好的研究算法对这些噪声参数的敏感性。

原始情况

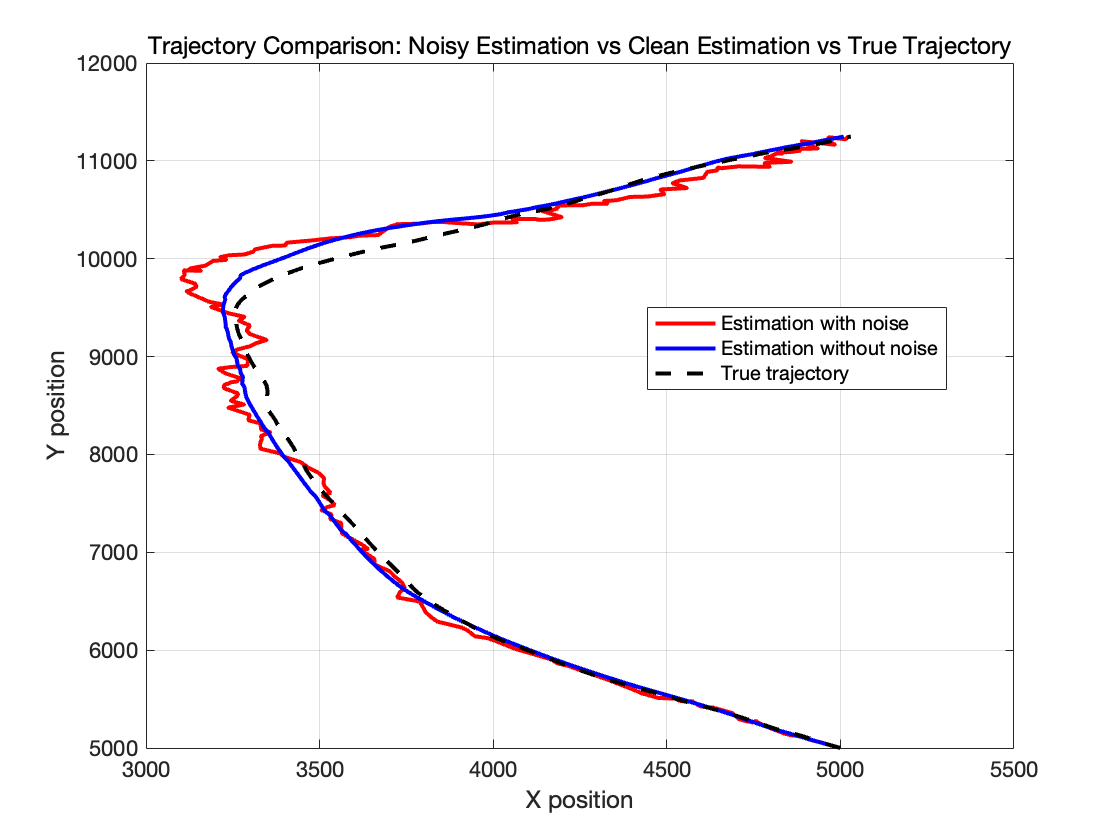
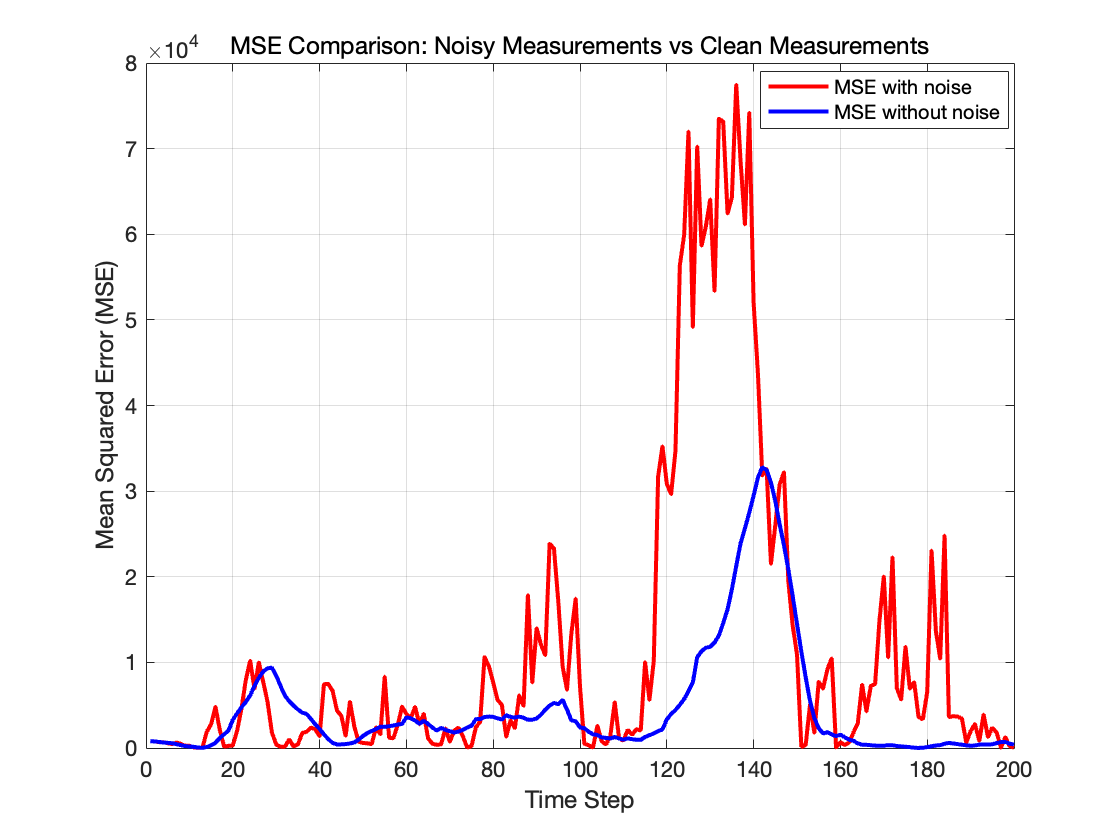
1. 接下来我们改变初始值，我们设置 (\sigma_u=[5;5], \sigma_r=100, \sigma_\theta=\pi/10)，即同时增大这些噪声，我们得到结果如下

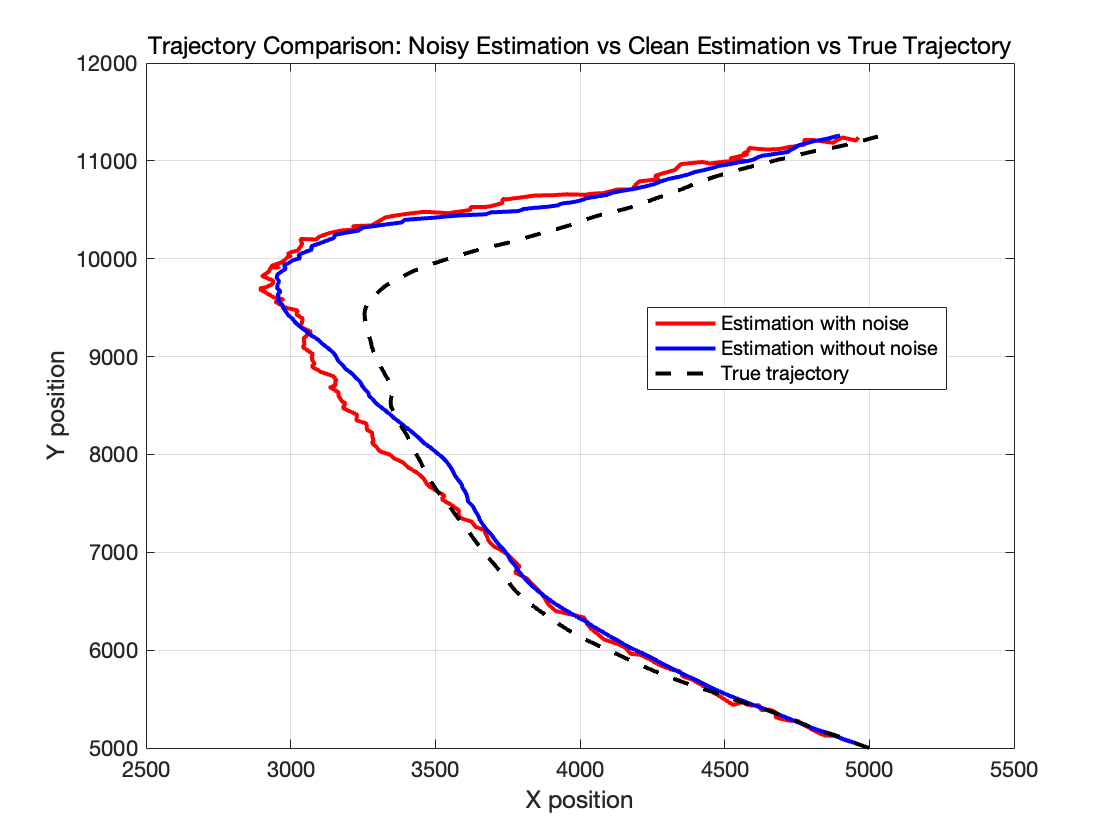
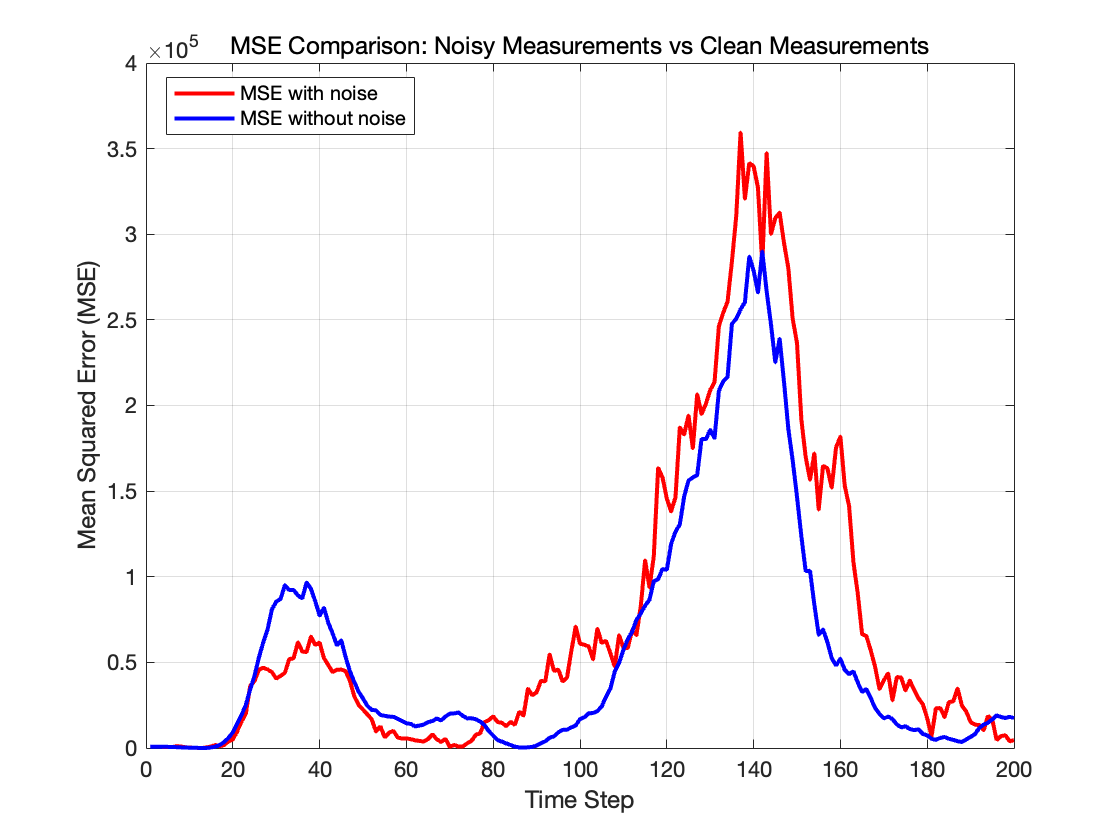
可见，这组参数使粒子滤波的估计偏差明显变大，这时因为这组参数值太大了，无论是过程噪声还是测量噪声，都给滤波带来了过度的随机性，导致难以准确收敛。

加速度噪声标准差 \sigma_u过大

将加速度噪声标准差从原先的2 提高到5，意味着在预测步骤（ \mathbf{x}(k)=\Phi,\mathbf{x}(k-1) + G,\mathbf{u}(k-1) ）中，每个粒子加入的随机扰动幅度显著增加。

距离测量噪声\sigma_r 过大

\sigma_r=100 表示雷达距离测量存在非常高的不确定性，粒子滤波器难以依靠测距迅速纠正过程预测的误差。

角度测量噪声\sigma_\theta 过大

将\sigma_\theta 提高到\pi/10（约18 度）意味着雷达观测的方位角精准度大幅下降，特别在转弯时，滤波器很难依据测角来纠正粒子分布。

综上所述，由于三组噪声值偏大，导致滤波结果很差，因此我们再分析当它们很小的时候来进行比较。

2. 我们设置(\sigma_u=[1;1], \sigma_r=20, \sigma_\theta=\pi/200)，即同时减小这些噪声，我们得到结果如下。

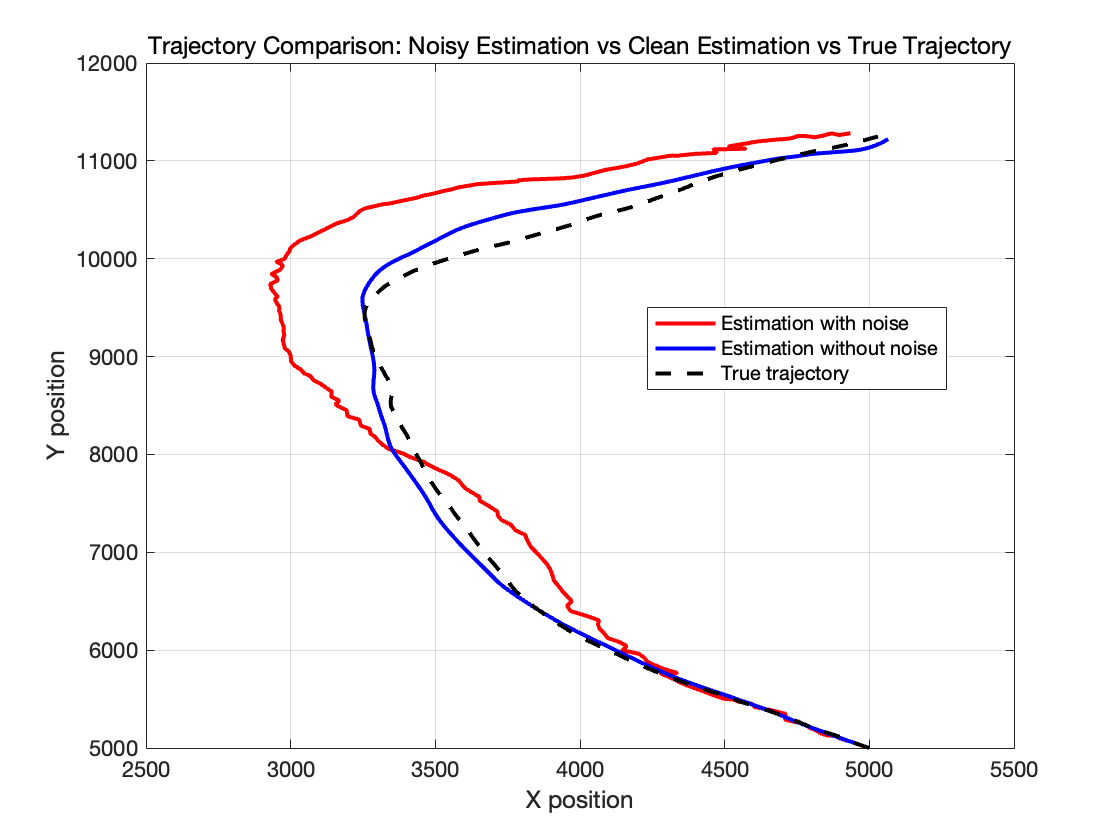
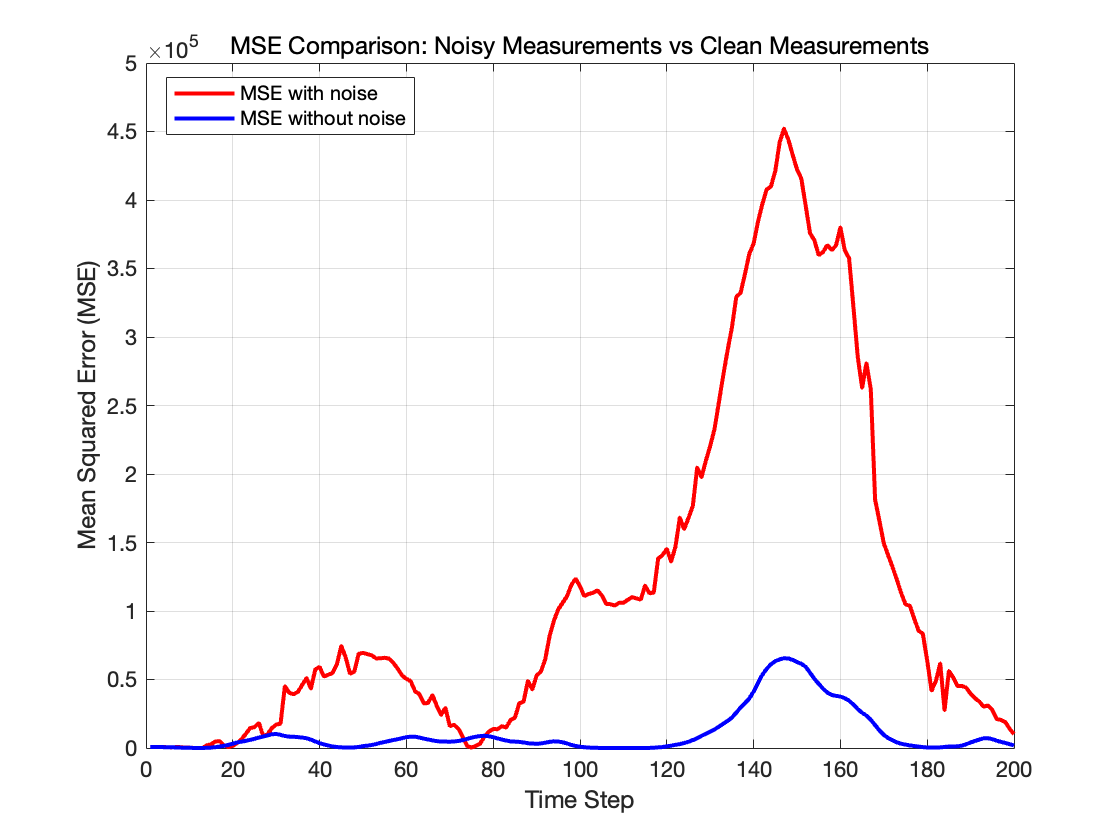
我们可以看见，估计结果也非常差，这是因为：

• 过程噪声\sigma_u 过小，意味着滤波器认为目标加速度波动很小、运动较为平稳，但是在转弯处目标发生了较大的机动，滤波器会因为预测过于保守而无法跟上真实轨迹，造成误差增大。

• 测量噪声\sigma_r 和\sigma_\theta 过小，导致过度信赖观测值，一旦观测有异常值，就会导致大偏差。

因此，三个初始化参数的选择需要平衡调节，比如说，如果目标运动激烈，则增大\sigma_u，让滤波器的预测更加灵活；如果对应路段运动平稳，可以减小\sigma_u 以减少抖动。

3. 通过最终调整到最佳参数，在无噪声数据的情况下，粒子滤波器可以完美估计真实轨迹。

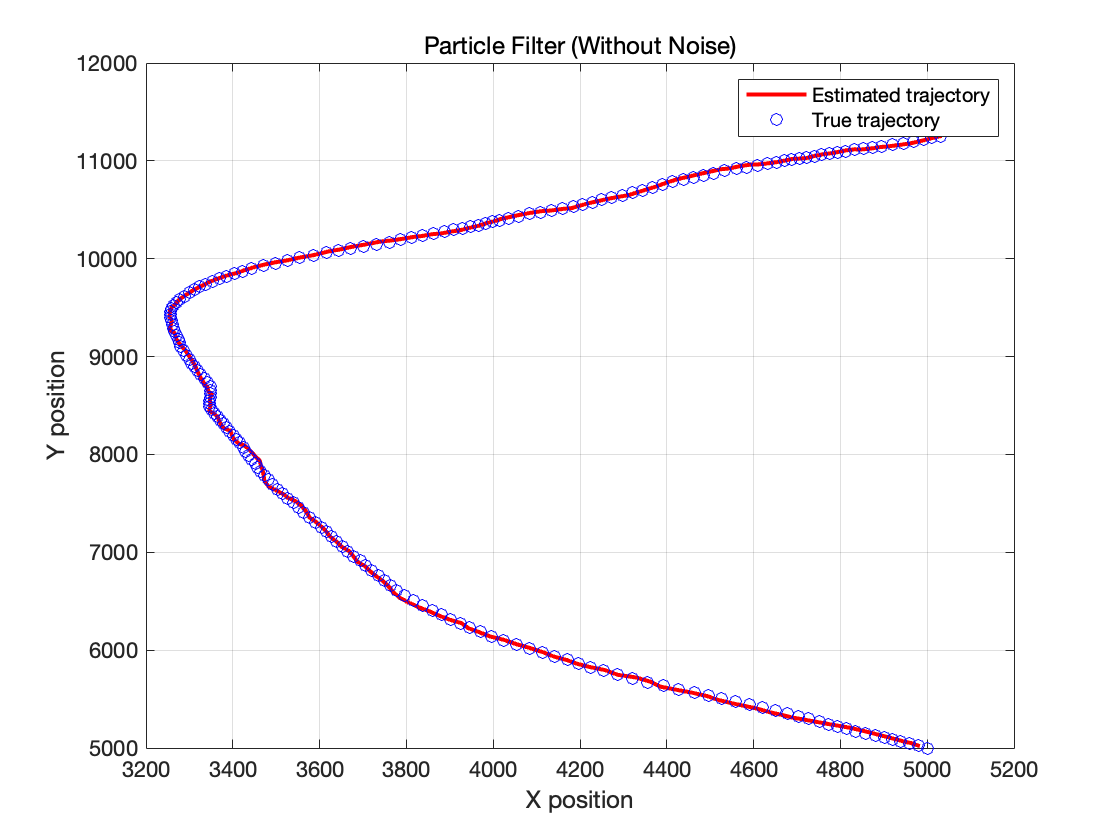
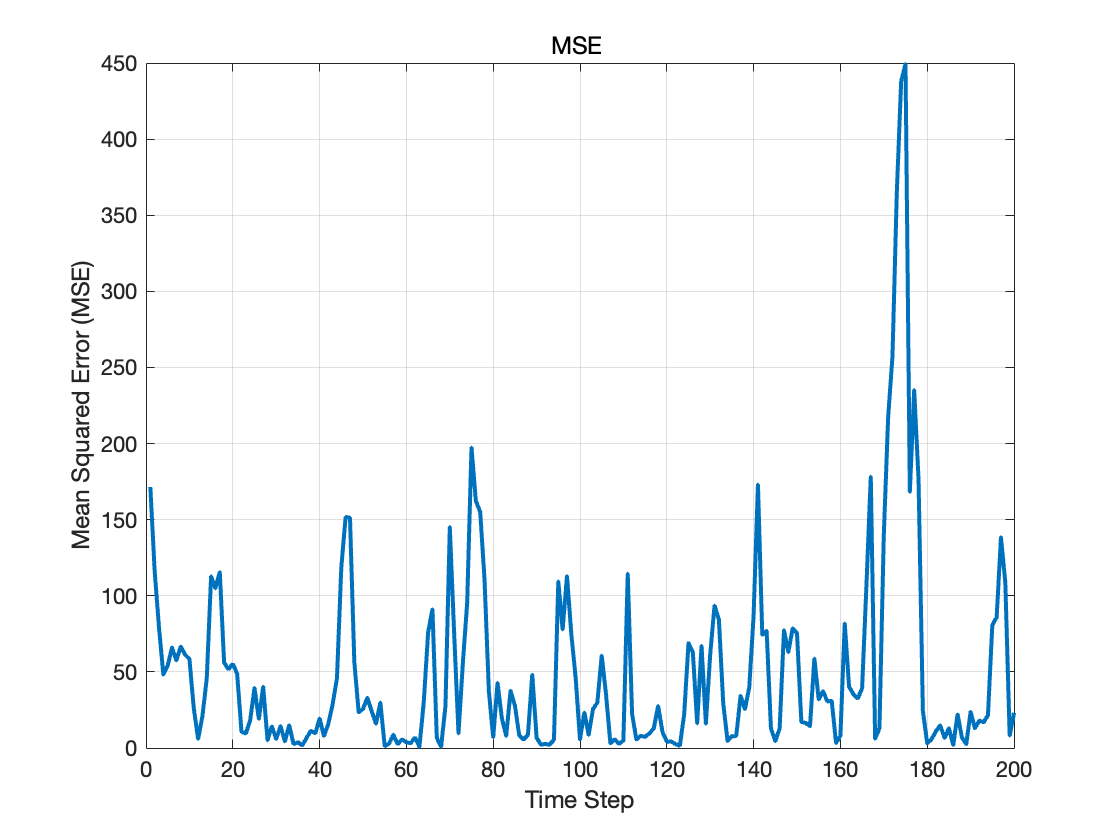
可以看到，滤波器的估计轨迹几乎与真实轨迹重合，且均方误差（MSE）很小。此外，在转弯时对状态的估计也非常精准。

完整代码

close all
clc
clear all

%% 参数定义
T = 1;                   % 时间步长
N = 1000;                % 粒子数
sigma_u = [2; 2];        % 过程噪声的标准差 (x 和 y 方向的加速度噪声)
sigma_r = 50;            % 距离测量噪声标准差
sigma_theta = pi/100;    % 角度测量噪声标准差

%% 数据加载
% 加载带噪声的雷达测量数据 
load('mesures_radar.mat');  
Z_noise = Z;  % 带噪声数据

% 加载无噪声的雷达测量数据 (这里重命名为  Z_clean )
load('mesures_radar_non_bruitees.mat');  
Z_clean = Z;  % 无噪声数据

% 加载真实轨迹数据 ( Xvrai )
load('trajectoire_reelle.mat');  

num_steps = size(Z_noise, 2);  % 时间步数

%% 初始化粒子
% 为保证比较一致，采用相同的初始化方式：
% 使用真实初始状态  Xvrai(:,1)  加上一定范围内的随机扰动
x_particles_noise = Xvrai(:, 1) * ones(1, N) + (rand(4, N) - 0.5) .* [5; 5; 1; 1];
x_particles_clean = Xvrai(:, 1) * ones(1, N) + (rand(4, N) - 0.5) .* [5; 5; 1; 1];

% 初始化权重（均匀分布）
weights_noise = ones(1, N) / N;
weights_clean = ones(1, N) / N;

% 存储滤波器的估计状态
estimated_states_noise = zeros(4, num_steps);
estimated_states_clean = zeros(4, num_steps);

% 计算状态转移矩阵  Phi  和加速度影响矩阵  G 
[Phi, G] = matrices_etat(T);

%% 粒子滤波主循环（带噪声测量数据）
for k = 1:num_steps
    % 预测：更新每个粒子的状态
    for i = 1:N
        x_particles_noise(:, i) = simu_modele_etat(x_particles_noise(:, i), Phi, G, sigma_u);
    end
    
    % 更新：根据似然函数更新权重（使用当前时间步的带噪声测量  Z_{noise}(:,k) ）
    for i = 1:N
        weights_noise(i) = vraisemblance(...
            x_particles_noise(1, i), x_particles_noise(3, i), ...
            Z_noise(1, k), Z_noise(2, k), sigma_r, sigma_theta);
    end
    weights_noise = weights_noise / sum(weights_noise);
    
    % 估计状态：加权平均
    estimated_states_noise(:, k) = x_particles_noise * weights_noise';
    
    % 重采样：判断有效粒子数  N_{eff} = 1/\sum_{i=1}^{N}w_i^2 
    Neff = 1 / sum(weights_noise.^2);
    if Neff < 0.95 * N
        [x_particles_noise, weights_noise] = resampling(x_particles_noise, weights_noise);
    end
end

%% 粒子滤波主循环（无噪声测量数据）
for k = 1:num_steps
    % 预测：更新每个粒子的状态
    for i = 1:N
        x_particles_clean(:, i) = simu_modele_etat(x_particles_clean(:, i), Phi, G, sigma_u);
    end
    
    % 更新：根据似然函数更新权重（使用当前时间步的无噪声测量  Z_{clean}(:,k) ）
    for i = 1:N
        weights_clean(i) = vraisemblance(...
            x_particles_clean(1, i), x_particles_clean(3, i), ...
            Z_clean(1, k), Z_clean(2, k), sigma_r, sigma_theta);
    end
    weights_clean = weights_clean / sum(weights_clean);
    
    % 估计状态：加权平均
    estimated_states_clean(:, k) = x_particles_clean * weights_clean';
    
    % 重采样：判断有效粒子数
    Neff = 1 / sum(weights_clean.^2);
    if Neff < 0.95 * N
        [x_particles_clean, weights_clean] = resampling(x_particles_clean, weights_clean);
    end
end

%% 绘制轨迹
figure;
% 绘制带噪声测量下滤波得到的轨迹（红色）
plot(estimated_states_noise(1, :), estimated_states_noise(3, :), 'r-', 'LineWidth', 2);
hold on;
% 绘制无噪声测量下滤波得到的轨迹（蓝色）
plot(estimated_states_clean(1, :), estimated_states_clean(3, :), 'b-', 'LineWidth', 2);
% 绘制真实轨迹（黑色虚线）
plot(Xvrai(1, :), Xvrai(3, :), 'k--', 'LineWidth', 2);
legend('滤波估计（带噪声）', '滤波估计（无噪声）', '真实轨迹', 'Location', 'best');
xlabel('X 位置');
ylabel('Y 位置');
title('轨迹比较：带噪声估计 vs 无噪声估计 vs 真实轨迹');
grid on;

%% 计算均方误差 (MSE)
% 对于带噪声情况，比较真实状态与估计状态（取  x  和  y  分量，即第1行和第3行）
erreur_noise = Xvrai([1,3], :) - estimated_states_noise([1,3], :);
mse_noise = vecnorm(erreur_noise, 2, 1).^2;

% 对于无噪声情况
erreur_clean = Xvrai([1,3], :) - estimated_states_clean([1,3], :);
mse_clean = vecnorm(erreur_clean, 2, 1).^2;

%% 绘制 MSE 曲线
figure;
plot(1:num_steps, mse_noise, 'r-', 'LineWidth', 2);
hold on;
plot(1:num_steps, mse_clean, 'b-', 'LineWidth', 2);
xlabel('时间步');
ylabel('均方误差 (MSE)');
title('MSE 比较：带噪声 vs 无噪声');
legend('带噪声 MSE', '无噪声 MSE', 'Location', 'best');
grid on;

%% 第四题示例：向无噪声测量添加自定义测量噪声并进行粒子滤波

close all;
clc;
clear all;

%========== 1) 设定你想加入的测量噪声（示例值） ======================
sigma_r_test = 20;          % 距离噪声标准差 (单位: m)
sigma_theta = deg2rad(0.01); % 角度噪声标准差 (单位: rad)

%========== 2) 加载无噪声测量 ============================================
load('mesures_radar_non_bruitees.mat'); 
% 假设其中包含 Z，维度为 2×(时间步数)
% Z(1,:) = 无噪声距离
% Z(2,:) = 无噪声角度

%========== 3) 添加噪声，生成 Z_bruite ====================================
Z_bruite = zeros(size(Z));
for k = 1:size(Z, 2)
    r_true = Z(1, k);     
    theta_true = Z(2, k); 
    
    % 添加测量噪声
    r_noise = r_true + randn(1)*sigma_r_test;
    theta_noise = theta_true + randn(1)*sigma_theta;
    
    % 生成带噪声测量
    Z_bruite(:, k) = [r_noise; theta_noise];
end

%========== 4) 加载真实轨迹（用于对比/计算误差） ========================
load('trajectoire_reelle.mat'); 
% 假设 trajectoire_reelle.mat 中有 Xvrai (4×timeSteps):
% Xvrai(1,:) = 真实 x
% Xvrai(2,:) = 真实 vx
% Xvrai(3,:) = 真实 y
% Xvrai(4,:) = 真实 vy

%========== 5) 粒子滤波主程序 =============================================
% 你也可以自行改动过程噪声、粒子数等参数
T = 1;                % 时间步长
N = 1000;             % 粒子数
sigma_u = [2; 2];     % 过程噪声标准差 (x、y方向加速度噪声)

% 此处使用我们刚才定义的测量噪声参数
sigma_r = sigma_r_test;
sigma_theta = sigma_theta;

% 载入我们已经写好的函数：matrices_etat、vraisemblance、simu_modele_etat、resampling
% 假设它们都在同一路径下或已添加路径

% 获取 Z_bruite 的时间步
num_steps = size(Z_bruite, 2);

% 初始化粒子 (将真实的初始状态复制 N 份)
x_particles = Xvrai(:, 1) * ones(1, N);

% 初始化权重
weights = ones(1, N) / N;

% 用于存储各时刻的估计结果
estimated_states = zeros(4, num_steps);

% 获取状态转移矩阵和加速度影响矩阵
[Phi, G] = matrices_etat(T);

%========== 粒子滤波循环 =============================================
for k = 1 : num_steps
    
    %----(1) 预测每个粒子的下一个状态
    for i = 1 : N
        x_particles(:, i) = simu_modele_etat(x_particles(:, i), Phi, G, sigma_u);
    end
    
    %----(2) 基于似然函数更新权重
    for i = 1 : N
        weights(i) = vraisemblance( ...
            x_particles(1, i), x_particles(3, i), ...
            Z_bruite(1, k),    Z_bruite(2, k), ...
            sigma_r, sigma_theta);
    end
    
    %----(3) 归一化权重
    weights = weights / sum(weights);
    
    %----(4) 计算加权平均作为估计结果
    estimated_states(:, k) = x_particles * weights';
    
    %----(5) 判断是否进行重采样
    Neff = 1 / sum(weights.^2);
    if Neff < 0.95 * N
       [x_particles, weights] = resampling(x_particles, weights);
    end
    
end

%========== 6) 绘图：粒子滤波估计轨迹 vs. 真实轨迹 =======================
figure;
plot(estimated_states(1, :), estimated_states(3, :), 'r-', 'LineWidth', 2); 
hold on;
plot(Xvrai(1, :), Xvrai(3, :), 'bo');  
legend('Estimated trajectory', 'True trajectory');
xlabel('X position');
ylabel('Y position');
title('Particle Filter (With Custom Noise)');
grid on;

%========== 7) 计算并绘制MSE，查看不同时间步的误差 =======================

% 计算均方误差（MSE）
mse_values = mean((estimated_states - Xvrai).^2, 1);

% 绘制MSE曲线
figure;
plot(1:num_steps, mse_values, 'LineWidth', 2);
xlabel('Time Step');
ylabel('Mean Squared Error (MSE)');
title('MSE of Particle Filter different initial values');
grid on;

参数可以自己改