线性回归是统计建模方法，用于建立自变量和因变量之间线性关系，是最基本的回归分析方法之一，用于解释变量之间的关系并进行预测。

一元线性回归

线性回归本质上是监督学习中的回归算法，用于对连续数值的预测。监督学习就是给定一堆数据，然后想办法让计算机学习出一个能预测新数据的模型。我们拿最简单的一维线性回归举例（回归 Regression 值的是预测量有倾向于回归到平均值），假设输出 y 跟输入 x 是线性关系，如下

y = mx + b

m 和 b 分别就是斜率和截距

为了让这个模型能拟合实际数据，就需要对模型进行训练，也就是要找出让预测结果最准确的 m 和 b （最优）。这个好坏评判标准就是 损失函数，也称为代价函数（模型犯错的代价），常见的就是均方误差(MSE)。

比如对于 N 个样本，真实值是 y_i ，模型预测值是 \hat{y}_i ，那么损失函数可以写成：

L(\hat{y}_i, y_i) = (\hat{y}_i - y_i)^2

如果想要所有样本的整体误差，就把它们求平均：

\frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)^2

训练模型的目的就是让这个整体误差最小，也就是找到让 \frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)^2 最小的 m 和 b 。这在数学上通常记作：

(m^*, b^*) = \arg \min_{m, b} \frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)^2

为什么要用平方而不是绝对值呢？因为平方曲线有最小值，尤其是它的导数好算，我们能用求导（或梯度下降法等）快速找到最优解。

最小二乘法求解最优参数

先定义损失函数

L(m,b) = \frac{1}{N} \sum_{i=1}^N \bigl(m x_i + b - y_i\bigr)^2

分别对 m 和 b 求偏导，并令它们等于0（想找最小值）

\begin{aligned} \frac{\partial}{\partial m} L(m, b) &= \frac{2}{N} \sum_{i=1}^{N} x_i (m x_i + b - y_i) \\ &= 2m \left(\frac{1}{N} \sum_{i=1}^{N} x_i^2 \right) + 2b \left(\frac{1}{N} \sum_{i=1}^{N} x_i \right) - 2 \left(\frac{1}{N} \sum_{i=1}^{N} x_i y_i \right)\\ \\ \frac{\partial}{\partial b} L(m, b) &= \frac{2}{N} \sum_{i=1}^{N} (m x_i + b - y_i) \\ &= 2m \left(\frac{1}{N} \sum_{i=1}^{N} x_i \right) + 2b - 2 \left(\frac{1}{N} \sum_{i=1}^{N} y_i \right) \end{aligned}

为了简化方程表达，引入以下符号假设:

x 的平均值: \bar{x} = \frac{1}{N}\sum_{i=1}^N x_i
y 的平均值: \bar{y} = \frac{1}{N}\sum_{i=1}^N y_i
x 方向上的方差: s^2 = \frac{1}{N}\sum_{i=1}^N x_i^2
x 和 y 的相关程度: \rho = \frac{1}{N}\sum_{i=1}^N x_i y_i

得到最优解:

\begin{cases} m^* = \frac{\sum_{i=1}^N (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^N (x_i - \bar{x})^2}=\frac{\rho - \bar{x} \bar{y}}{s^2 - \bar{x}^2} \\ b^* = \bar{y} - m^*\bar{x} \end{cases}

一元线性回归思想: 先假设一个线性模型，然后让损失函数最小，解出让代价最小的那一条线，也就是那一组参数

多元线性回归

现在我们把情况扩展到多元，即多个因素（特征 feature）共同影响 y 。假设我们有 D 个特征(因变量)，每个特征记为 x_{i,d} ，第 i 个样本，第 d 个特征。

因此多元模型可以写成如下形式:

y_i = b + \sum_{d=1}^D w_d x_{i,d}

y_i 是第 i 个样本的真实值， b 是偏置(bias)， w_d 是与特征 x_{i,d} 对应的权重

有时候我们会把 b 写成 w_0 ，同时把 x_{i,0} 固定为1，这样公式可以统一为向量内积的形式：

y_i = w_0x_{i,0} + \sum_{d=1}^D w_d x_{i,d} = \sum_{d=0}^D w_d x_{i,d} = \underline{w}^T \underline{x}_i

如果我们有 n 条训练样本，每条样本包含 D 个特征，那么可以将所有样本的特征放到一个 n \times (D+1) 的矩阵 X 里(多出的那一列对应 x_{i,0} = 1 )。权重向量 w 则是一个 (D+1) 维的列向量，目标值 y 是一个 n 维的列向量。具体形式如下：

\underline{X} = \begin{bmatrix} x_{1,0} & x_{1,1} & x_{1,2} & \dots & x_{1,D} \\ x_{2,0} & x_{2,1} & x_{2,2} & \dots & x_{2,D} \\ \vdots & \vdots & \vdots & & \vdots \\ x_{n,0} & x_{n,1} & x_{n,2} & \dots & x_{n,D} \end{bmatrix},\quad \underline{w} = \begin{bmatrix} w_0 \\ w_1 \\ \vdots \\ w_D \end{bmatrix},\quad \underline{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}

对于每条样本 i ，有 y_i = \underline{w}^T \underline{x}_i 。把所有样本合并后，就可以写成矩阵形式：

\underline{y} = \underline{X} \cdot \underline{w}

接下来我们继续构建损失函数和应用最小二乘法来求解最优参数向量 \underline{w} :

L(\underline{w}) = \frac{1}{N} \sum_{i=1}^N \bigl(y_i - \underline{w}^T \underline{x}_i\bigr)^2 = \frac{1}{N} \| \underline{X}\cdot \underline{w} - \underline{y} \|^2

让模型预测值 \underline{X} \cdot \underline{w} 与真实值 \underline{y} 之间的欧几里得距离最小。

L(w) 对 w 求偏导等于0:

\frac{\partial L(\underline{w})}{\partial \underline{w}} = \frac{2}{N} \underline{X}^T (\underline{X} \underline{w} - \underline{y}) = 0

得到:

\underline{X}^T \underline{X} \underline{w} = \underline{X}^T \underline{y}

如果 \underline{X}^T \underline{X} 可逆，那么可以直接求解 \underline{w} ：

\underline{w} = (\underline{X}^T \underline{X})^{-1} \underline{X}^T \underline{y}

这个结果公式称之为 Normal Equation

对于简单理论我们能求解析解，但是实际应用中数据量级非常大，特别是求逆矩阵的复杂度在 O(n^3) 级别，所以这时就需要用梯度下降法来近似求解，好处是速度大幅度提升，坏处是不一定得到绝对最优解。

线性回归使用场景

安斯库四重奏 (Anscombe’s Quartet)

安斯库四重奏 (Anscombe’s Quartet) 展示了四组不同分布的数据，尽管这四组数据在均值、方差、回归线等统计指标上都相同，但其实际散点分布形态却完全不同。

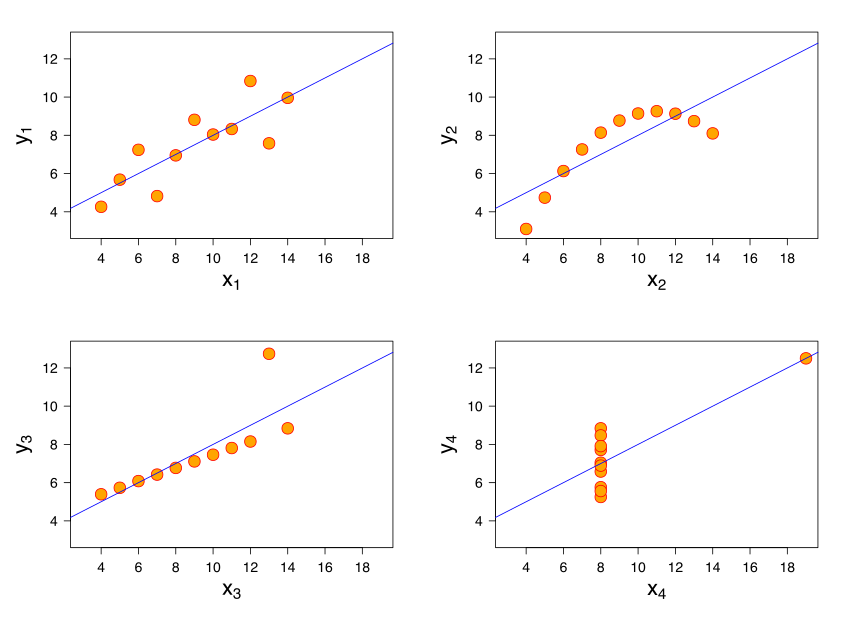
这说明，使用线性回归并不能只单纯依赖数据的基本统计量，必须考察数据本身的分布、离群点等。具体需要遵循以下这几个要求:

1.回归问题与分类问题

同时，要分清楚回归(regression)和分类(classification)两个不同的机器学习任务:

回归：预测的是连续型数值，例如房价、温度、身高等。
分类：预测的是离散型类别，例如判断邮件是否垃圾邮件，图片中物体属于哪种类别等。

只有当要预测的目标是连续型变量时，才能使用线性回归等回归模型。

2. 变量之间是线性关系

线性回归最核心的假设之一是自变量 x 和因变量 y 之间存在线性关系，如果数据是非线性关系，就需要先做特征变换(如对数变换、多项式特征等)先变换到线性关系，或使用其他非线性模型。

3. 误差服从均值为0的正态分布

经典线性回归(最小二乘法)的一个重要前提，即实际观测值 y_i 偏离 x_i 程度（残差）是随机且符合分布 N(0, \sigma^2)

4. 变量 x 的分布要接近正态分布

希望自变量 x 本身的分布也尽量接近正态，以便更好地满足线性回归的相关推断条件(如置信区间、假设检验等)。如果数据较大情况下，中心极限定理可能发挥一定作用。否则如果 x 的分布过于极端或者很偏，会影响模型的稳定性。

5. 多元线性回归中不同特征之间相互独立

当回归扩展到多元情形时，需要关注特征(自变量)之间的多重共线性(multi-collinearity)问题。理想情况下，不同特征之间应相对独立，不要存在较高的相关性。因此，在使用多元线性回归前，往往需要先做特征选择、降维(如主成分分析)或正则化(如岭回归、Lasso)等手段来减弱多重共线性带来的影响。

推广 -- 广义线性模型

我们从另一个角度来重看线性回归模型，假设自变量因变量之间是线性关系，即

Y = X\beta + \varepsilon, \quad \varepsilon \sim \mathcal{N}(0, \sigma^2)

线性回归的假设为：

因变量 Y 服从正态分布，即: Y \sim \mathcal{N}(\mu, \sigma^2)
误差项（残差）也服从均值为 0 的正态分布，即: \mathcal{N}(0, \sigma^2)
线性预测子 \eta 和 Y 之间是直接的线性关系。

对于第三个假设我们暂且不考虑，我们现在只关注正态分布的问题，也就是说现在 Y 和误差都卡在正态分布这里，如果实际数据不服从正态分布会怎么样？该怎么做？这就是广义线性模型的思路。

广义线性模型（GLM）就是为了突破线性回归对正态分布的限制，允许 Y 和偏差服从其他分布（指数分布族），但是这样就存在几个问题:

(1). 之前线性回归模型 Y = X\beta + \varepsilon 就不能再使用了，因为如果数据服从二项分布，Y 只能取 0 或 1 ，那和连续的回归预测问题本质不是冲突了吗？再或者取柏松分布，Y 只能取非负整数，负数整个丢掉了，回归居然无法预测负数，这就没法玩了。

(2). 线性回归假设误差项的方差是固定的，这在正态分布里没问题，但是到了柏松分布里，均值 E(Y)增大时，方差 Var(Y) 也增大; 亦或者二项分布里，方差取决于均值p(1−p)，不恒定

(3). 线性回归使用最小二乘法来求偏导为0得最优解，但是最小二乘法是基于正态分布的最大似然估计，如果 Y 服从非正态分布，就需要对应分布的最大似然估计方法

为了解决以上这几个问题，链接函数由此而生，我们不再局限于将 Y 和 Xβ 之间用偏差 \varepsilon 来线性关系建模，而是将Y 的均值 E(Y) 和线性预测子 Xβ 之间用一个链接函数关联起来。

g(E(Y))=Xβ

对于(1)的解决: 连接函数 g(μ) 作用在 E(Y) 上，而不是直接建模 Y

如果是二项分布（逻辑回归），链接函数取：
g(\mu) = \log \frac{\mu}{1 - \mu}
这样就把 μ 从 (0,1) 映射到整个实数范围 (−∞,+∞)
如果是柏松分布（泊松回归），链接函数取：
g(μ)=log(μ)
保证 μ 始终为正数，避免预测负值的问题。

因此对数函数调整了因变量 Y 的取值范围。未做完，有疑问

Zehua